2024成都中考数学第一轮专题复习之第三章 微专题 函数的实际应用 教学课件

这是一份2024成都中考数学第一轮专题复习之第三章 微专题 函数的实际应用 教学课件，共34页。PPT课件主要包含了课标要求，考情及趋势分析，第1题图，第2题图，200－a，a≥200，≤a≤800，由题意得，解题关键点，第3题图等内容，欢迎下载使用。
1.结合具体情境体会一次函数的意义，能用一次函数解决简单实际问题；2.结合具体情境体会反比例函数的意义，能用反比例函数解决简单实际问题；3.通过对实际问题的分析，体会二次函数的意义；4.会求二次函数的最大值或最小值，并能确定相应自变量的值(2022年版课标新增)，能解决相应的实际问题．
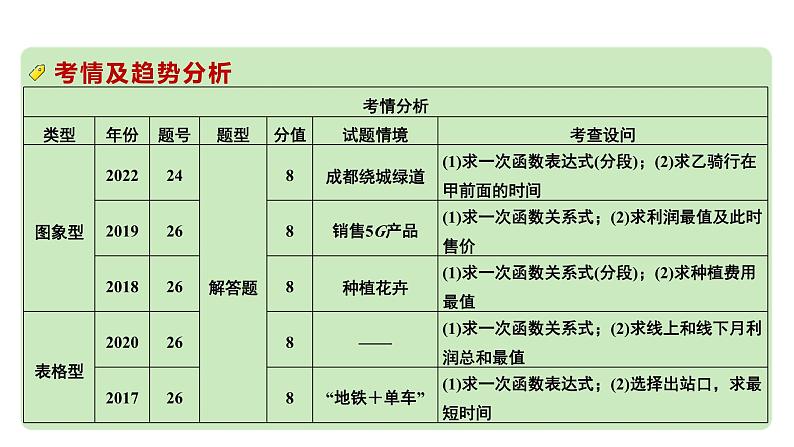
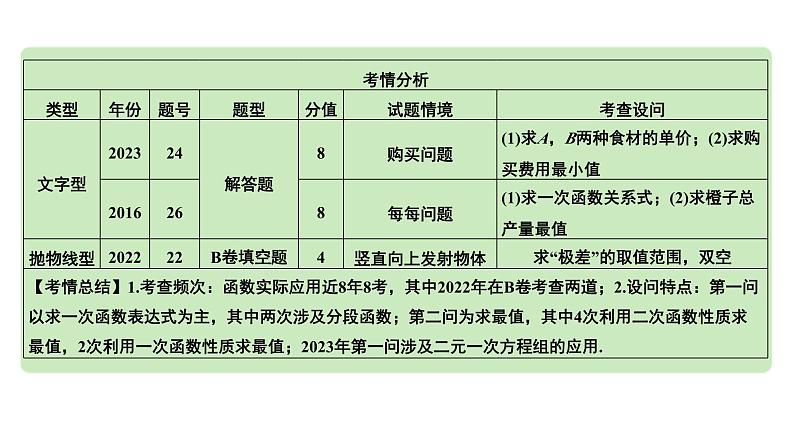
类型一　图象型(8年3考：2022.24，2019.26，2018.26)
1. (2022成都B卷24题8分)随着“公园城市”建设的不断推进，成都绕城绿道化身成为这座城市的一个超大型“体育场”，绿道骑行成为市民的一种低碳生活新风尚．甲、乙两人相约同时从绿道某地出发同向骑行，甲骑行的速度是18 km/h，乙骑行的路程s(km)与骑行的时间t(h)之间的关系如图所示．(1)直接写出当0≤t≤0.2和t＞0.2时，s与t之间的函数表达式；
【解法提示】当0≤t≤0.2时，设s＝kt，将(0.2，3)代入，得3＝0.2k，解得k＝15，∴s＝15t；当t＞0.2时，设s＝k′t＋b，将(0.2，3)，(0.5，9)代入，
∴s＝20t－1.综上所述，s与t之间的函数表达式为s＝ .
得 解得
解：(1)s与t之间的函数表达式为s＝ ；
(2)何时乙骑行在甲的前面？
(2)当0≤t≤0.2时，易得18t＞15t；当t＞0.2时，20t－1＞18t，解得t＞0.5.∴0.5小时后乙骑行在甲前面．
分析函数图象(1)首先要读懂函数图象中的横、纵坐标代表的量；(2)拐点：图象上的拐点，既是前一段函数图象的终点，又是后一段函数图象的起点，反映函数图象在这一时刻开始发生变化；(3)水平线：函数值随自变量的变化而保持不变；(4)交点：表示两个函数的自变量与函数值分别对应相等，这个交点是函数值大小关系的“分界点”．
【解法提示】当0≤x≤300时，设y＝kx，将(300，39 000)代入，得k＝130，∴y＝130x；当x>300时，设y＝k1x＋b，将(300, 39 000)，(500，55 000)代入，
2. (2018成都B卷26题8分)为了美化环境，建设宜居成都，我市准备在一个广场上种植甲、乙两种花卉．经市场调查，甲种花卉的种植费用y(元)与种植面积x(m2)之间的函数关系如图所示，乙种花卉的种植费用为每平方米100元．(1)直接写出当0≤x≤300和x＞300时，y与x的函数关系式；
得 解得 即y＝80x＋15 000，∴y与x的函数关系式为y＝
解：(1)y与x的函数关系式为y＝ ；
(2)广场上甲、乙两种花卉的种植面积共1 200 m2，若甲种花卉的种植面积不少于200_m2①，且不超过乙种花卉种植面积的2倍②，那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少？最少总费用为多少元？
设广场上甲种花卉的种植面积为a m2，则乙种花卉的种植面积为_________m2；由题中①可得关系式__________；由题中②可得关系式_______________；联立两个关系式求出甲种花卉的种植面积范围为_____________；根据总费用＝甲种花卉的种植费用＋乙种花卉的种植费用列出函数关系式，利用第(1)问求得的函数关系式和一次函数性质求解即可．
a≤2(1 200－a)
(2)设甲种花卉的种植面积为a m2，则乙种花卉的种植面积为(1 200－a)m2，种植总费用为W元，
解得200≤a≤800.当200≤a≤300时，W1＝130a＋100(1 200－a)＝30a＋120 000，∵30>0，∴W1随a的增大而增大，∴当a＝200时，W最小＝126 000；当300＜a≤800时，W2＝80a＋15 000＋100(1 200－a)＝－20a＋135 000，∵－20