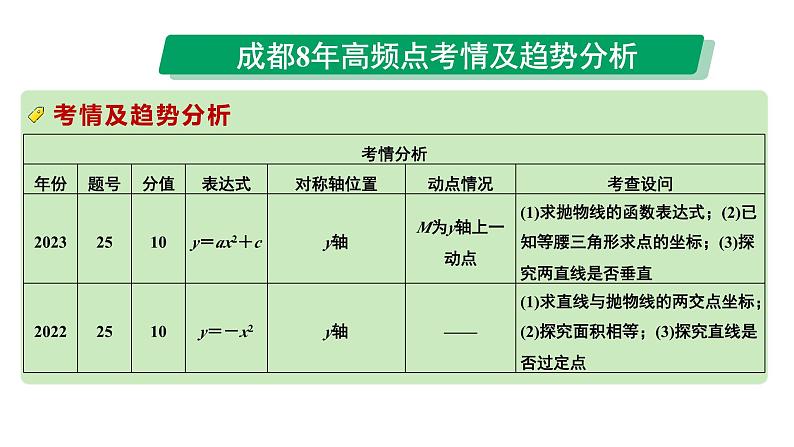
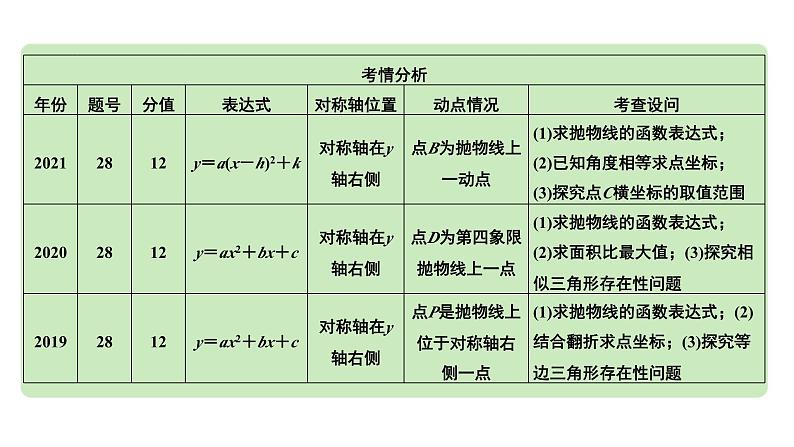
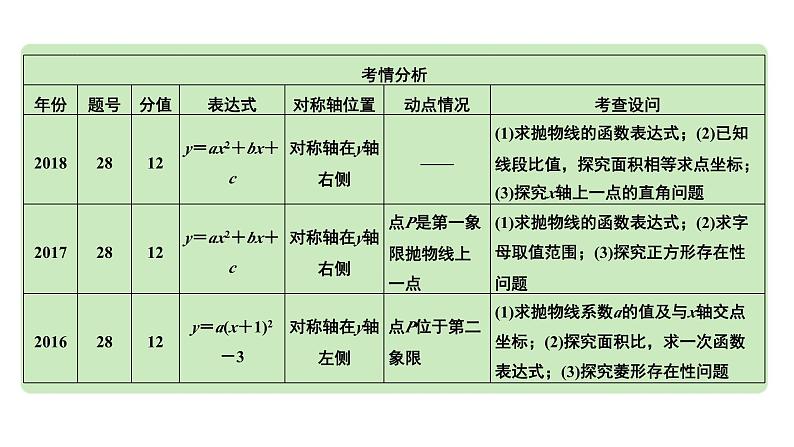
2024成都中考数学第一轮专题复习之第三章 微专题 二次函数综合题 类型一~二 教学课件

这是一份2024成都中考数学第一轮专题复习之第三章 微专题 二次函数综合题 类型一~二 教学课件，共36页。PPT课件主要包含了考情及趋势分析，例题图①，例题图②，例题图③，例题图④，例题解图④，方法四和差法，例题图⑤，解题关键点，解题有策略等内容，欢迎下载使用。
类型一　线段问题(2023.25)
例 　 已知抛物线y＝－x2＋bx＋c与x轴交于A(－1，0)，B两点，与y轴交于点C(0，3)，连接BC.(1)如图①，点D是x轴上一点，连接CD，若AD＝CD，求点D的坐标；
【思维教练】设出点D的坐标，线段AD的长可以根据横坐标相减得到，线段CD的长可以根据C，D两点的坐标利用勾股定理得到，然后结合线段相等列方程求解即可．
解：(1)设D(d，0)，∵A(－1，0)，C(0，3)，∴AD＝|d＋1|，OC＝3，∴CD＝ ＝ .∵AD＝CD，∴|d＋1|＝ ，即(d＋1)2＝9＋d2，解得d＝4，∴点D的坐标为(4，0)；
(2)如图②，点E是抛物线对称轴上一动点，连接AE，CE，求AE＋CE的最小值；
【思维教练】根据抛物线的对称性可知关于抛物线对称轴对称的两个点到抛物线对称轴上的任意一点的距离相等，连接BE，可知AE＝BE，从而将问题转化成求BE＋CE的最小值，根据三点共线时线段和最短即可求解．
(2)将点A(－1，0)，C(0，3)分别代入y＝－x2＋bx＋c中，
得 解得
∵C(0，3)，∴OC＝3，OB＝3，∴BC＝ ＝3 .∵点E在抛物线的对称轴上，∴AE＝BE，∴AE＋CE＝BE＋CE.∵BE＋CE≥BC，∴当B，C，E三点共线时，BE＋CE取得最小值，最小值为BC的长．∴AE＋CE的最小值为3 ；
∴抛物线的函数表达式为y＝－x2＋2x＋3＝－(x－1)2＋4，∴抛物线的对称轴为直线x＝1，∴B(3，0).如图，连接BE，
(3)如图③，点P是第一象限内抛物线上一点，连接OP交BC于点F.①当 时，求点P的坐标；
【思维教练】根据相似三角形的性质可知相似三角形对应边成比例，过点P作PM∥y轴交CB于点M，从而将 转化成 ，根据线段长的比例列出关系式求解即可．
①如图，过点P作PM∥y轴，交BC于点M，设P(t，－t2＋2t＋3).
∵B(3，0)，C(0，3)，∴直线BC的表达式为y＝－x＋3，∴M(t，－t＋3)，∴PM＝－t2＋2t＋3－(－t＋3)＝－t2＋3t.∵PM∥y轴，∴△OCF∽△PMF，
∴－t2＋3t＝2，解得t1＝1，t2＝2，∴点P坐标为(1，4)或(2，3)；
∴ ，∴ ，
【思维教练】由①可知 ，用 表示出 ，再利用二次函数的性质即可求解最值．
②探究 有最大值吗？若有，求出最大值，若没有，请说明理由；
② 有最大值．理由如下：由①知 ＝ ＝－ t2＋t＝－ (t－ )2＋ ∵－ ＜0，∴ 有最大值，最大值是 ；
【思维教练】过点P作PF∥y轴，交BC于点F，根据抛物线的性质可得△OBC是等腰直角三角形，从而得到△FPQ也是等腰直角三角形，根据等腰直角三角形直角边与斜边的关系，将求PQ的最大值转化成求PF的最大值，设出点P的坐标，从而表示出点F的坐标，进而表示出PF的长，根据二次函数的性质即可求解．
(4)如图④，点P是第一象限内抛物线上一点，过点P作PQ⊥BC于点Q，求PQ的最大值及此时点P的坐标；
(4)如图，过点P作PF∥y轴，交BC于点F，
∵OB＝OC＝3，∴∠OCB＝45°.∵PF∥y轴，∴∠PFQ＝∠OCB＝45°，∴PQ＝ PF，∵B(3，0)，C(0，3)，∴直线BC的表达式为y＝－x＋3.设P(n，－n2＋2n＋3)，则F(n，－n＋3)，∴PF＝－n2＋2n＋3－(－n＋3)＝－n2＋3n，
∴PQ＝ PF＝－ n2＋ n＝－ (n－ )2＋ ，
∴－ ＜0，0