2024成都中考数学第一轮专题复习之第五章 第二节 矩形、菱形、正方形的性质与判定 教学课件

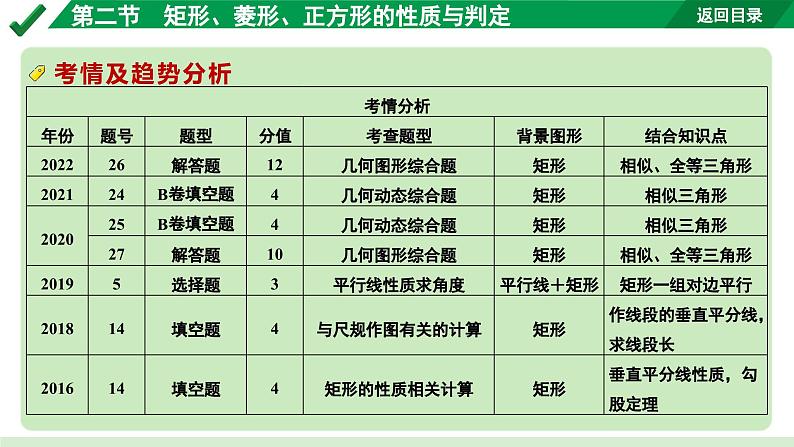
这是一份2024成都中考数学第一轮专题复习之第五章 第二节 矩形、菱形、正方形的性质与判定 教学课件，共60页。PPT课件主要包含了课标要求，考情及趋势分析，平分且垂直，一组对角，知识关联，例1题图①，答案25°，例1题图②，例1题图③，例1题图④等内容，欢迎下载使用。
命题点1　矩形的性质与判定(8年7考)1.理解矩形的概念；2.探索并证明矩形判定定理：三个角是直角的四边形是矩形，对角线相等的平行四边形是矩形；3.探索并证明矩形的性质定理：矩形的四个角都是直角，对角线相等．
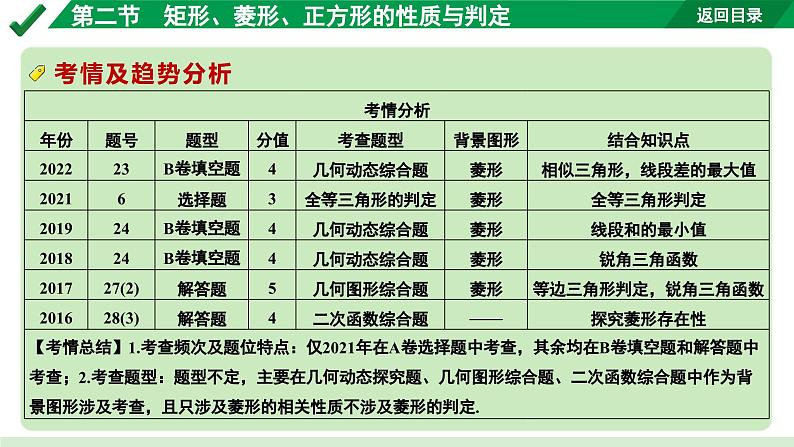
命题点2　菱形的性质与判定(8年6考)1.理解菱形的概念；2.探索并证明菱形的判定定理：四边相等的四边形是菱形，对角线互相垂直的平行四边形是菱形；3.探索并证明菱形的性质定理：菱形的四条边相等，对角线互相垂直．
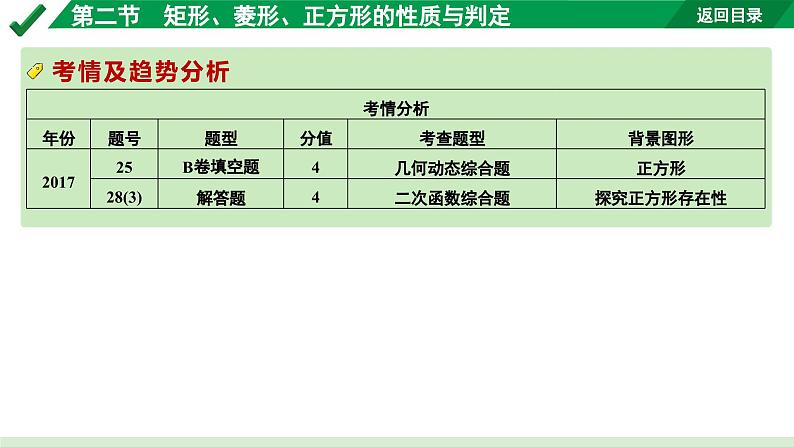
命题点3　正方形的性质与判定(8年2考)1.理解正方形的概念，以及它们之间的关系；2.正方形具有矩形和菱形的一切性质．(2022年版课标细化)
矩形、菱形、正方形的性质与判定
【拓展知识】中点四边形
1.定义：依次连接任意一个四边形各边的中点所得的四边形叫做中点四边形2.常见结论
①特殊四边形可类比三角形特殊化的过程进行研究；②特殊平行四边形可在平行四边形的基础上进行探究，需理清平行四边形和特殊平行四边形的关联和区别．
例1　 已知四边形ABCD为矩形．(1)如图①，连接BD，以点B为圆心，AB长为半径画弧，交BD于点E，交BC于点F，连接AE，EF.若∠BEF＝70°，则∠DAE的度数是________；
【解法提示】∵四边形ABCD是矩形，∴∠BAD＝∠ABC＝90°.∵BE＝BF＝BA，∴∠BFE＝∠BEF＝70°，∠BAE＝∠BEA，∴∠EBF＝180°－∠BEF－∠BFE＝40°，
∴∠ABE＝90°－∠EBF＝50°，∴∠BAE＝∠BEA＝(180°－∠ABE)÷2＝65°，∴∠DAE＝90°－∠BAE＝25°.
(2)如图②，设AC，BD交于点O，E为AD的中点．若AB＝6，BC＝8，则△BOE的周长为________；
【解法提示】∵四边形ABCD是矩形，∴AB＝CD＝6，AD＝BC＝8.∵O是AC的中点，E为AD的中点，∴OE＝ CD＝3，AE＝ AD＝4，在Rt△ABE中，根据勾股定理得，BE＝ ，在Rt△ABD中，根据勾股定理得，BD＝ .∵点O是BD的中点，∴BO＝ BD＝5，∴△BOE的周长为5＋3＋2 ＝8＋2 .
(3)如图③，设AC，BD交于点O，过点O作EF⊥BD交AD于点E，交BC于点F，若AB＝3，BC＝4，则AE的长为________；
【解法提示】如图，连接BE，
∵四边形ABCD是矩形，∴∠ADC＝90°，CD＝AB＝3，AD＝BC＝4，OB＝OD.∵EF⊥BD，∴DE＝BE，设AE＝x，则DE＝BE＝4－x，在Rt△ABE中，由勾股定理得x2＋32＝(4－x)2，解得x＝ ，即AE＝ .
(4)如图④，连接BD，过点A作AE⊥BD，垂足为E，连接CE.若∠ADB＝30°，则cs ∠DEC的值为__________；
【解法提示】如图，过点C作CF⊥BD于点F，
设CD＝2a，∵四边形ABCD为矩形，∴AB∥CD，AB＝CD，∴∠ABE＝∠CDF，在△ABE与△CDF中， ∴△ABE≌△CDF(AAS)，∴AE＝CF，BE＝DF.∵∠BAD＝90°，∠ADB＝30°，
∴∠ABD＝60°，BD＝2AB＝4a.∵AE⊥BD，∴∠BAE＝30°，∴BE＝FD＝ AB＝a，AE＝CF＝ a，EF＝4a－2a＝2a，在Rt△CEF中，CE＝ ，∴cs ∠DEC＝ .
过点C作BD的垂线，通过三角形全等，得到∠DEC所在的直角三角形的边之间关系，求出cs的值；
(5)如图⑤，E是BC的中点，F是CD边上任意一点．若AB＝6，BC＝8，则AE＝________，当△AEF的周长最小时，点E到AF的距离为________；
【解法提示】如图，作点E关于直线CD的对称点E′，连接AE′交CD于点F，作EH⊥AF于点H.
∵四边形ABCD是矩形，AB＝6，BC＝8，E是BC的中点，∴BE＝CE＝CE′＝ BC＝4.∵CD∥AB，∴△E′FC∽△E′AB，∴ ，即 ，解得CF＝2，∴DF＝CD－CF＝6－2＝4，
∴AE＝ ，AF＝ .∵S△AEF＝ AF·EH＝S矩形ABCD－S△ABE－S△ADF－S△EFC，∴ ×4 ·EH＝6×8－ ×6×4－ ×4×2－ ×8×4＝16，∴EH＝ .
(6)如图⑥，E为BC上一点，将△ABE沿AE折叠，使点B落在点F处，连接CF.若AB＝6，BC＝8，当△CEF是直角三角形时，则线段BE的长为________；
【解法提示】当△CEF为直角三角形时，有两种情况：①当点F落在矩形内部时，如解图④，在Rt△ABC中，AB＝6，BC＝8，∴AC＝10.由折叠的性质得∠AFE＝∠B＝90°，EB＝EF，AB＝AF＝6，当△CEF为直角三角形时，只能得到∠EFC＝90°，∴A，F，C三点共线，∴CF＝10－6＝4，设BE＝x，则EF＝x，CE＝8－x，
在Rt△CEF中，∵EF2＋CF2＝CE2，∴x2＋42＝(8－x)2，解得x＝3，即BE＝3；②当点F落在AD边上时，如解图⑤，此时四边形ABEF为正方形，∴BE＝AB＝6.综上所述，BE的长为3或6.
△CEF为直角三角形需分点F落在矩形内部和边上两种情况讨论.
(7)如图⑦，若E，F分别是边BC，AD上的点，FD＝BE，连接AE，DE，BF，CF，BF交AE于点H，CF交DE于点P，若∠BFC＝90°，求证：四边形FPEH是矩形．
(7)证明：∵四边形ABCD为矩形，∴AD∥BC，AD＝BC.∵FD＝BE，∴AF＝EC，∴四边形AECF、四边形DFBE均为平行四边形，∴AE∥CF，BF∥ED，∴四边形FPEH为平行四边形．∵∠BFC＝90°，∴四边形FPEH是矩形．
例2　 已知四边形ABCD是菱形．(1)若∠BAD＝110°，则∠ABD的度数为________；
【解法提示】∵四边形ABCD为菱形，∴AB＝AD，∴∠ABD＝∠ADB.∵∠BAD＝110°，∴∠ABD＝ ＝35°.
(2)设AC与BD交于点O，若BD＝8，AC＝6，则菱形ABCD的周长为________，面积为________；
【解法提示】∵四边形ABCD是菱形，AC＝6，BD＝8，∴AO＝CO＝3，BO＝DO＝4，BD⊥AC，由勾股定理得BC＝ ＝5，∴菱形ABCD的周长为4×5＝20，菱形ABCD的面积为 ×8×6＝24.
(3)如图①，设AC与BD交于点O，过点A作AP⊥BC于点P，连接OP，若AB＝4，OP＝ ，则AP的长为________；
【解法提示】∵四边形ABCD为菱形，∴AB＝AD＝BC＝4，AO＝CO，AC⊥BD.∵AP⊥BC，∴OP为斜边AC的中线，∴AC＝2OP＝2 ，AO＝OC＝ ，由勾股定理得OD＝ ，∴BD＝2OD＝2 ，∴菱形ABCD的面积为BC·AP＝ AC·BD＝2 ，∴AP＝ .
(4)如图②，过点A作AE⊥BC于点E，F是AB的中点，连接EF，DF.若∠EFD＝90°，AB＝2，则cs ∠ABC的值为________；
【解法提示】如图，延长DF交CB的延长线于点G，连接DE.
∵四边形ABCD是菱形，∴AB＝BC＝AD＝2，AD∥CG，∴∠ADF＝∠G.∵F是AB的中点，∴AF＝BF.∵∠AFD＝∠GFB，∴△ADF≌△BGF，
∴BG＝AD＝2，GF＝DF.∵∠EFD＝90°，∴EG＝ED，设BE＝x.∵AE⊥BC，∴AE⊥AD，∴∠AEB＝∠EAD＝90°.∵AE2＝AB2－BE2＝DE2－AD2，即22－x2＝(2＋x)2－22，∴x＝ －1或－ －1(舍去)，即BE＝ －1，∴cs ∠ABC＝ .
(5)如图③，菱形ABCD的边长为4，过点A作AP⊥BC于点P，将菱形沿AP翻折，点B的对应点为E，AE交CD于点G，若菱形ABCD的面积为4 ，则EG的长为________；
【解法提示】∵菱形ABCD的边长为4，∴AB＝BC＝4，CD∥AB.由折叠的性质可知，PE＝BP，AE＝AB.∵AP⊥BC，∴折叠后点E落在BC的延长线上．∵菱形ABCD的面积为4 ，∴BC·AP＝4 ，∴AP＝ ，∴在Rt△ABP中，BP＝ ＝3，
∴PE＝3，CP＝BC－BP＝1，∴BE＝6，CE＝2.∵CD∥AB，∴∠GCE＝∠B.又∵∠E＝∠E，∴△GCE∽△ABE，∴ ，即 ，∴EG＝ .
(6)如图④，菱形ABCD的边长为4，过点A作AP⊥BC于点P，∠ABC＝60°，对角线AC与BD交于点O，点Q是BD上的一动点，连接CQ，PQ，则CQ＋PQ的最小值为________；
【解法提示】如图，连接QA，
∵四边形ABCD为菱形，∴点C关于BD的对称点为点A，∴QA＝QC，即CQ＋PQ＝AQ＋PQ≥AP，∴当A，Q，P三点共线时，CQ＋PQ取最小值，最小值为PA.∵∠ABC＝60°，AB＝BC，∴△ABC为等边三角形．
∵AP⊥BC，∴P为CB的中点，∴BP＝ BC＝2，∵AB＝4，∴PA＝ ＝2 ，即CQ＋PQ的最小值为2 .
(7)如图⑤，点E，F在对角线BD上(点E在点F左侧)，连接AE，AF，CE，CF，AE∥CF.求证：四边形AECF是菱形．
(7)证明：如图，连接AC交BD于点O，
∵AE∥CF，∴∠AED＝∠CFB.∵四边形ABCD是菱形，∴AD＝CB，AD∥CB，BD垂直平分AC，∴∠ADE＝∠CBF，AE＝CE，AF＝CF，∴△ADE≌△CBF(AAS)，∴AE＝CF，∴AE＝CE＝AF＝CF，∴四边形AECF是菱形．
例3　 已知四边形ABCD为正方形，点E为该正方形内一点．(1)如图①，若点E在BD上，点F在AB上，过点F作FG⊥BD，垂足为点G，若FE＝EC，EF⊥CE，OE＝3，则BF的长为________；
【解法提示】∵四边形ABCD是正方形，∴AC⊥BD，∠ABD＝45°.∵EF⊥CE，∴∠COE＝∠FEC＝90°，∴∠FEG＝90°－∠CEO＝∠ECO.∵FG⊥BD，∴∠EGF＝∠COE＝90°，在△EFG和△CEO中，
∴△EFG≌△CEO(AAS)，∴FG＝EO＝3.∵∠ABD＝45°，∴△FBG是等腰直角三角形，∴BF＝ FG＝3 .
(2)如图②，若点E在BD上，延长AE交CD于点P，连接CE，若PE＝PC，则∠DPE＝________；
【解法提示】∵四边形ABCD为正方形，E为对角线BD上一点，∴AD＝CD，∠ADC＝90°，∠ADE＝∠CDE＝45°.在△AED和△CED中，∴△AED≌△CED(SAS)，∴∠DAE＝∠DCE，设∠PCE＝α，则∠DAE＝α.
∵PE＝PC，∴∠PEC＝∠PCE＝α，∴∠DPE＝2α.∵∠DAE＋∠DPE＝90°，即3α＝90°，解得α＝30°，∴∠DPE＝60°.
证明△AED≌△CED，再结合PE＝PC推导出角度相等，利用三角形内外角关系求解．
(3)如图③，若点E在AC上，以DE为边作正方形DEFG，H是CD上一点，且DH＝ CD，连接GH，若AB＝3 ，则GH的最小值为________；
【解法提示】如图，连接CG，
∵四边形ABCD是正方形，四边形DEFG是正方形，∴DA＝DC＝AB＝3 ，DE＝DG，∠ADC＝∠EDG＝90°，∠DAC＝45°，∴∠ADE＝∠CDG，∴△ADE≌△CDG(SAS)，∴∠DCG＝∠DAE＝45°，∴点G的轨迹是射线CG，根据垂线段最短可知，当GH⊥CG时，GH的值最小．
∵DH＝ CD＝2 ，∴CH＝ CD＝ ，∴GH最小＝CH·sin 45°＝ × ＝1.
连接CG，通过证明全等三角形判断出点G的运动轨迹是关键．
(4)如图④，若点E在AC上，点F在AD上，且DF＝2，G为BC的中点，AB＝6，则EF－EG的最大值是________；
【解法提示】如解图②，取CD的中点G′，连接FG′，EG′.
∵四边形ABCD是正方形，BG＝GC，CG′＝CG，∴点G与点G′关于AC对称，∴EG＝EG′，在Rt△DFG′中，FG′＝ .∵EF－EG＝EF－EG′≤FG′，即当F，G′，E三点共线时，EF－EG取最大值，最大值为FG′，∴EF－GE的最大值为 .
(5)如图⑤，对角线AC，BD相交于点E，∠F＝90°，FD＝FC.求证：四边形DECF是正方形．
(5)证明：∵四边形ABCD是正方形，∴∠EDC＝∠DCE＝45°.∵∠F＝90°，FD＝FC，∴∠FDC＝∠FCD＝45°，∴∠ECF＝∠EDF＝∠F＝90°，∴四边形DECF是矩形．∵DF＝CF，∴四边形DECF是正方形．
四边形的相关计算中，与三角形有关的知识：1. 勾股定理：当题干中给出线段长和线段垂直(90°)或隐含的直角时，考虑利用勾股定理求解．注：隐含的垂直有：(1)矩形、正方形中的四个角均为90°；(2)菱形、正方形的对角线互相垂直；(3)直径对直角．2. 锐角三角函数：(1)已知特殊角(30，45°，60)或三角函数值，构造直角三角形，利用锐角三角函数求解；
(2)隐含特殊角，特殊四边形的对角线平分两组对角，如正方形的对角线将两组对角分别平分成两个45°角．3. 全等三角形：(1)由特殊四边形的对边平行，可得角相等；(2)特殊四边形的对边相等；(3)根据题干中的已知条件再找一组等边(或一对等角)可得三角形全等，如对顶角、中点、角平分线、垂直平分线等，可得两个三角形全等．
1. 如图，在菱形ABCD中，∠A＝60°，E，H分别为AB，AD的中点，F，G分别为CE，BH的中点，若线段GF的长为2 ，则AB的长为_______．
【解析】如图，连接BF并延长交CD于点M，连接MH.
∵四边形ABCD为菱形，∠A＝60°，∴AB∥CD，∴∠D＝120°，∠MCF＝∠BEF.∵点F为CE的中点，∴CF＝EF.∵∠CFM＝∠EFB，∴△CFM≌△EFB(ASA)，∴MF＝BF，CM＝EB＝ CD＝ AB，
∴点M为CD的中点，F为BM的中点．∵G为BH的中点，∴FG是△BMH的中位线，∴FG＝ MH，∴MH＝2FG＝4 .∵H，M分别为AD，CD的中点，∴DH＝DM.∵∠D＝120°，∴MH＝ DH＝4 ，∴DH＝4，∴AD＝2DH＝8，∴AB＝8.
2. 如图，在正方形ABCD中，O为AC，BD的交点，△DCE为直角三角形，∠CED＝90°，OE＝3 ，若CE·DE＝6，则正方形ABCD的面积为________．
【解析】如图，过点O作OM⊥CE交EC的延长线于点M，作ON⊥DE于点N，
∵∠CED＝90°，∴四边形OMEN是矩形，∴∠MON＝90°，∵四边形ABCD是正方形，O为AC，BD的交点，∴∠COD＝90°.
∵∠COM＋∠CON＝∠DON＋∠CON，∴∠COM＝∠DON.∵四边形ABCD是正方形，∴OC＝OD，在△COM和△DON中， ∴△COM≌△DON(AAS)，∴OM＝ON，CM＝DN，∴四边形OMEN是正方形．∵OE＝3 ，∴NE＝ON＝ OE＝ ×3 ＝3.
∵DE＋CE＝DN＋NE＋CE＝CM＋NE＋CE＝EN＋EM＝2EN＝6，设DE＝a，CE＝b，∴a＋b＝6.∵CE·DE＝6，CD2＝a2＋b2＝(a＋b)2－2ab＝62－2×6＝24，∴S正方形ABCD＝24.
由题干可得到∠DOC＝∠DEC＝90°，OD＝OC，属于典型的“对角互补”模型.
3. 如图，已知四边形ABCD，点Q为AB左侧平面内一点，连接BQ，DQ，AQ，且∠BQD＝∠BAD.(1)如图①，当四边形ABCD是菱形，且∠C＝60°时，求∠AQD的度数；
解：(1)如图，在DQ上截取DE＝BQ，连接AE，设AB，DQ相交于点F.
∵∠BQD＝∠BAD＝∠C＝60°，∠QFB＝∠AFD，∴∠QBA＝∠ADE.∵四边形ABCD是菱形，∴AB＝AD.∵BQ＝DE，∴△QAB≌△EAD(SAS)，
∴∠BAQ＝∠DAE，AQ＝AE.∵∠BAQ＋∠EAF＝∠DAE＋∠EAF＝∠BAD＝60°，∴△AQE是等边三角形，∴∠AQD＝60°；
(2)如图②，当四边形ABCD是正方形时，请探究线段AQ，BQ，DQ之间的数量关系；
(2)如图，过点A作AE⊥AQ交DQ于点E，设DQ，AB相交于点F.
∵四边形ABCD是正方形，∴∠BQD＝∠BAD＝90°，AB＝AD.∵∠QFB＝∠AFD，∴∠QBA＝∠EDA.∵AE⊥AQ，∴∠EAQ＝90°，∴∠BAQ＋∠BAE＝∠BAE＋∠DAE＝90°，
∴∠BAQ＝∠DAE，∴△QAB≌△EAD(ASA)，∴BQ＝DE，AQ＝AE，∴△AQE为等腰直角三角形，∴EQ＝ AQ，∴DQ＝EQ＋DE＝ AQ＋BQ，即DQ＝ AQ＋BQ；
(3)如图③，当四边形ABCD是矩形，且AD∶AB＝ 时，请探究线段AQ，BQ，DQ之间的数量关系．
(3)如图，过点A作AE⊥AQ交DQ于点E，设DQ，AB交于点F.
∵四边形ABCD是矩形，∴∠BQD＝∠BAD＝90°.∵∠QFB＝∠AFD，∴∠QBA＝∠EDA.∵∠QAE＝∠BAD＝90°，∴∠QAB＝∠EAD，∴△QAB∽△EAD，∴ ，
∴DE＝ BQ，tan ∠AQE＝ ，∴∠AQE＝60°，∴∠AEQ＝30°，∴EQ＝2AQ，∴DQ＝EQ＋DE＝2AQ＋ BQ，即DQ＝2AQ＋ BQ.
矩形的性质与判定 8年7考，常在尺规作图题、几何动态探究题、几何图形综合题中作为背景图形考查
1. (2016成都14题4分)如图，在矩形ABCD中，AB＝3，对角线AC，BD相交于点O，AE垂直平分OB于点E，则AD的长为________．
1．1变设问——求面积 如图，在矩形ABCD中，AD＝9，对角线AC与BD相交于点O，AE⊥BD，垂足为E，若DE＝3BE，则矩形ABCD的面积为________．