2024成都中考数学第一轮专题复习之专题四 几何动态探究题 教学课件

这是一份2024成都中考数学第一轮专题复习之专题四 几何动态探究题 教学课件，共49页。PPT课件主要包含了考情及趋势分析，类型一动点探究题，第1题图，第2题图，°或84°，第3题图，第4题图，解题关键点，第6题图，第7题图等内容，欢迎下载使用。

(8年2考：2022.23，2020.25)
1. (2023武侯区二诊)如图，在等边△ABC中(其中AB＞ )，点P在AB边上运动，点Q在BC边上运动，且满足PQ＝6(点P，Q都不与B重合)，以PQ为底边在PQ左侧作等腰△PQD，使得∠PDQ＋∠B＝180°，则四边形PDQB面积的最大值是________．
2．我们定义：在一个三角形中，若一个角的度数是另一个角度数的7倍，则这样的三角形称之为“德馨三角形”．如：三个内角分别为100°，70°，10°的三角形是“德馨三角形”．如图，E为△ABC的边AC上一动点，连接BE，作∠AEB的平分线交AB于点D，在BE上取点F，使∠BFD＋∠BEC＝180°，∠EDF＝∠C.若△BCE是“德馨三角形”，则∠C的度数为 ______________.
3. 如图，在菱形ABCD中，对角线AC，BD交于点O，P是BD上一动点，点E在BC上，且BC＝3CE，若AC＝6，BD＝ ，则PC＋PE的最小值为________．
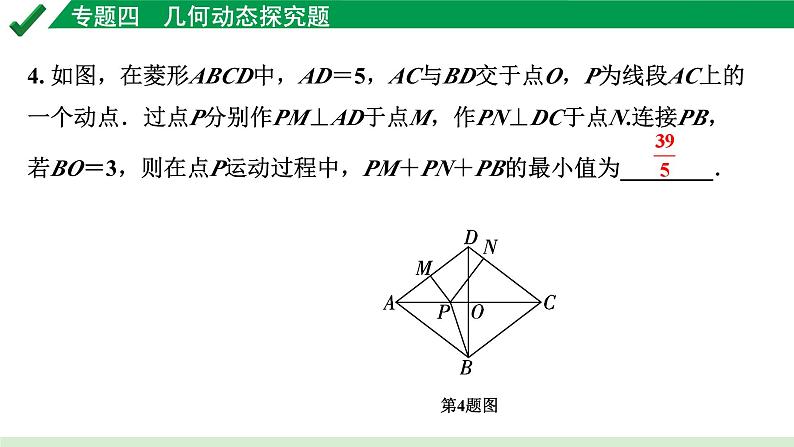
4. 如图，在菱形ABCD中，AD＝5，AC与BD交于点O，P为线段AC上的一个动点．过点P分别作PM⊥AD于点M，作PN⊥DC于点N.连接PB，若BO＝3，则在点P运动过程中，PM＋PN＋PB的最小值为________．
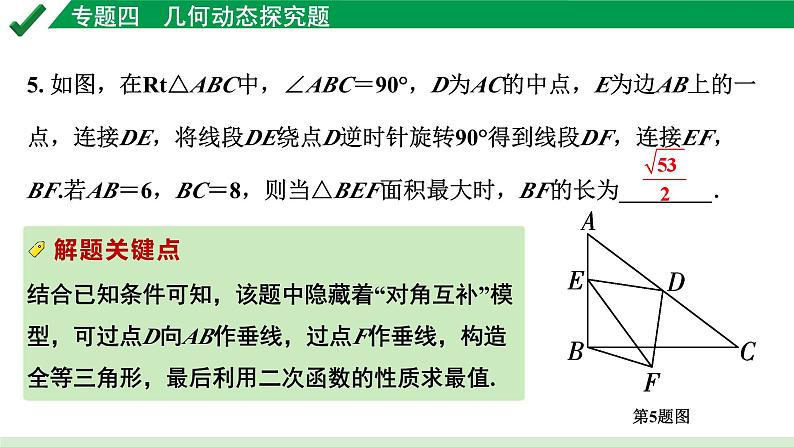
5. 如图，在Rt△ABC中，∠ABC＝90°，D为AC的中点，E为边AB上的一点，连接DE，将线段DE绕点D逆时针旋转90°得到线段DF，连接EF，BF.若AB＝6，BC＝8，则当△BEF面积最大时，BF的长为________．
结合已知条件可知，该题中隐藏着“对角互补”模型，可过点D向AB作垂线，过点F作垂线，构造全等三角形，最后利用二次函数的性质求最值.
6. (2023陕西)如图，在矩形ABCD中，AB＝3，BC＝4.点E在边AD上，且ED＝3，M，N分别是边AB，BC上的动点，且BM＝BN，P是线段CE上的动点，连接PM，PN.若PM＋PN＝4，则线段PC的长为________．
7. (北师九上P19第2题改编)如图，在矩形ABCD中，AD＝6，AE⊥BD，垂足为E，ED＝3BE，动点P，Q分别在BD，AD上，则AE的长为______，AP＋PQ的最小值为________．
8. (2023泸州)如图，E，F是正方形ABCD的边AB的三等分点，P是对角线AC上的动点，当PE＋PF取得最小值时， 的值是 ________．
9. 如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，M是AB的中点，动点P以每秒1个单位长度的速度从点A向点C运动，与此同时，动点Q以每秒2个单位长度的速度从点C向点B运动，当其中一个点运动到终点时，另一个点也随之停止运动，则△MPQ面积的最小值为________.
10. (2023金牛区模拟)如图，已知四边形ABCD是矩形，AB＝8，AD＝12，点E是线段DC上一个动点，分别以DE，EC为边向线段DC的下方作正方形DEFG、正方形CEHI，连接GI，过点B作直线GI的垂线，垂足是J，连接AJ，则点E运动过程中，线段AJ的最大值是____________.
【解析】如解图，取GI中点P，连接PB，以PB为直径作⊙O，连接AO并延长交⊙O于点J，作OM⊥AG于点M，作PQ⊥AB于点Q，交OM，DC于点N，K，
∴PK是梯形DGIC中位线．
∵DC＝8，∴PK＝ (CI＋DG)＝4.∵P是GI中点，∴P到DG，CI的距离均为4，∴P一定是以DC为边的正方形的中心点，∴点J一定在以BP为直径的圆上运动，∴当AJ过圆心O时，AJ最大．∵AB＝8，∴QB＝4.
∵AD＝12，∴PQ＝16.∵QB＝4，∴BP＝ ＝4 ，∴OJ＝2 .∵PQ＝16，∴QN＝AM＝8.∵ON＝ QB＝2，∴OM＝6，∴AO＝ ＝10，∴AJ＝10＋2 .
11. (2022龙东地区)如图，菱形ABCD中，对角线AC，BD相交于点O，∠BAD＝60°，AD＝3，AH是∠BAC的平分线，CE⊥AH于点E，点P是直线AB上的一个动点，则OP＋PE的最小值是________．
12. (2022成都B卷23题4分)如图，在菱形ABCD中，过点D作DE⊥CD交对角线AC于点E，连接BE，点P是线段BE上一动点，作P关于直线DE的对称点P′，点Q是AC上一动点，连接P′Q，DQ.若AE＝14，CE＝18，则DQ－P′Q的最大值为________．
13. (2020成都B卷25题4分)如图，在矩形ABCD中，AB＝4，BC＝3，E，F分别为AB，CD边的中点．动点P从点E出发沿EA向点A运动，同时，动点Q从点F出发沿FC向点C运动，连接PQ，过点B作BH⊥PQ于点H，连接DH.若点P的速度是点Q的速度的2倍，在点P从点E运动至点A的过程中，线段PQ长度的最大值为________，线段DH长度的最小值为__________．
14. (2023新都区模拟)如图，在边长为6的等边△ABC中，动点E在AB边上(与点A，B均不重合)，点F在边AC上，且AF＝BE，CE与BF相交于点G，连接AG.当点E在AB边上运动时，求AG的最小值．
解：如解图，过点A作AD∥BC，过点C作CD∥AB.
∵△ABC是等边三角形，∴四边形ABCD是菱形，∠ABC＝60°，∴∠BAD＝120°，BC＝AD，∠DAC＝60°，∴∠DAF＝∠CBE.
∵BE＝AF，∴△ADF≌△BCE(SAS)，∴DF＝CE，∠BCE＝∠ADF.∵AB＝AD，∠BAF＝∠DAF，AF＝AF，∴△BAF≌△DAF(SAS)，∴∠ADF＝∠ABF，∴∠ABF＝∠BCE，∴∠BGC＝180°－(∠GBC＋∠GCB)＝180°－(∠GBC＋∠ABF)＝180°－∠CBE＝120°，如解图，作△BGC的外接圆O，即点G在以O为圆心，OB为半径的圆上运动，∴∠BOC＝120°.
∵OB＝OC，∴∠OBC＝∠OCB＝30°，连接AO，交⊙O于点G1，交BC于点M，即当A，G，O三点共线时，AG最小，AO是BC的垂直平分线，∴BM＝CM＝3，∴OM＝ ＝ .∵∠BCO＝30°，∴OC＝2 ，∠ACO＝90°，∴∠OAC＝30°，∵cs 30°＝ ＝ ＝ ，∴AO＝4 ，∴AG的最小值为AO－AG1＝AO－OC＝4 －2 ＝2 .
类型二　折叠探究题(8年5考：2023.22，2021.24，2018.24，2017.25，2016.25)
1. (2023成都B卷22题4分)如图，在Rt△ABC中，∠ABC＝90°，CD平分∠ACB交AB于点D，过D作DE∥BC交AC于点E，将△DEC沿DE折叠得到△DEF，DF交AC于点G.若 ＝ ，则tan A＝________．
【解析】如解图，过点G作GM⊥DE于点M.
∵CD平分∠ACB交AB于点D，DE∥BC，∴∠1＝∠2，∠2＝∠3，∴∠1＝∠3，∴ED＝EC.∵∠3＝∠4，∴∠1＝∠4.又∵∠DGE＝∠CGD，∴△DGE∽△CGD，∴ ＝ ，∴DG2＝GE·GC.
∵∠ABC＝90°，DE∥BC，则AD⊥DE，∴AD∥GM，∴ ＝ ，∠MGE＝∠A.∵ ＝ ＝ ，设GE＝3，AG＝7，EM＝3n，则DM＝7n，则EC＝DE＝10n.∵DG2＝GE·GC，∴DG2＝3×(3＋10n)＝9＋30n，在Rt△GMD中，GM2＝DG2－DM2，在Rt△GME中，GM2＝GE2－EM2，DG2－DM2＝GE2－EM2，
即9＋30n－(7n)2＝32－(3n)2，解得n＝ (不符合题意的值已舍去)，∴EM＝ .∵GE＝3，则GM＝ ＝ ＝ ，∴tan A＝tan ∠MGE＝ ＝ ＝ .
2. 如图，在正方形ABCD中，AB＝8，点E在AD上，将三角形ABE沿BE折叠，使点A的对应点G落在正方形内部，连接DG并延长交BC于点M，若M恰好为BC的中点，则AE的长为________．
3. (2021成都B卷24题4分)如图，在矩形ABCD中，AB＝4，AD＝8，点E，F分别在边AD，BC上，且AE＝3，按以下步骤操作：第一步，沿直线EF翻折，点A的对应点A′恰好落在对角线AC上，点B的对应点为B′.则线段BF的长为________；第二步，分别在EF，A′B′上取点M，N，沿直线MN继续翻折，使点F与点E重合，则线段MN的长为________．
4. (2018成都B卷24题4分)如图，在菱形ABCD中，tan A＝ ，M，N分别在边AD，BC上，将四边形AMNB沿MN翻折，使AB的对应线段EF经过顶点D，当EF⊥AD时， 的值为________．
5. (2017成都B卷25题4分)如图①，把一张正方形纸片对折得到长方形ABCD，再沿∠ADC的平分线DE折叠，如图②，点C落在点C′处，最后按图③所示方式折叠，使点A落在DE的中点A′处，折痕是FG.若原正方形纸片的边长为6 cm，则FG＝________ cm.
【解析】如解图，连接AA′，交EC′于点K，过点G作GM⊥AC′于点M，过点A′作A′H⊥AD于点H，
易知C′E＝MG＝AB＝AC′＝C′D＝3 cm，
由折叠的性质得GF⊥AA′，∴∠AFG＋∠C′AK＝90°，∠MGF＋∠AFG＝90°，∴∠MGF＝∠C′AK.∵∠FMG＝∠KC′A＝90°，MG＝C′A，∴△AKC′≌△GFM(ASA)，∴AK＝GF.
∵AC′＝3 cm，A′是DE的中点，A′H∥C′E，∴A′H＝ C′E＝ cm，
H是C′D的中点，△AHA′∽△AC′K，∴C′H＝1.5 cm，∴AH＝4.5 cm，∴ ＝ ，∴ ＝ ，∴C′K＝1 cm，在Rt△AC′K中，AK＝ ＝ cm，∴FG＝AK＝ cm.
6. (2016成都B卷25题4分)如图，面积为6的平行四边形纸片ABCD中，AB＝3，∠BAD＝45°，按下列步骤进行裁剪和拼图．第一步：如图①，将平行四边形纸片沿对角线BD剪开，得到△ABD和△BCD纸片，再将△ABD纸片沿AE剪开(E为BD上任意一点)，得到△ABE和△ADE；第二步：如图②，将△ABE纸片平移至△DCF处，将△ADE纸片平移至△BCG处；
第三步：如图③，将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合，△PQM与△DCF在DC的同侧)，将△BCG纸片翻转过来使其背面朝上置于△PRN处(边PR与BC重合，△PRN与△BCG在BC的同侧).则由纸片拼成的五边形PMQRN中，对角线MN的长度的最小值为________．
类型三　平移、旋转探究题(8年2考：2019.24，2016.25 )
1. 如图，在正方形ABCD中，AB＝4，将正方形沿对角线AC的方向剪开，再将△ABC沿对角线BD方向平移得到△EFG，若平移的距离为 ，则图中两个三角形重叠部分的面积为________．
2. 如图，△ABC和△ADE都是等边三角形，AB＝3，AD＝2，将△ADE绕点A顺时针旋转，连接BD，CD，CE，在△ADE绕点A顺时针旋转的过程中，△BCD的面积S的取值范围为____________________．
【解析】如解图①，过A作AH⊥BC于点H，
当AD与AH在同一条直线上，且点D在△ABC的外部时，△DBC的面积最大．
在等边△ABC中，∵AH⊥BC，∴BH＝CH＝ BC＝ ，∠BAH＝ ∠BAC＝30°，∴AH＝ BH＝ ，∴DH＝2＋ ，∴S最大＝ BC·DH＝ ×3×(2＋ )＝3＋ .
如解图②，当AD与AH在同一条直线上，且点D在△ABC的内部时，△DBC的面积最小，S最小＝ BC·DH＝ ×3×( －2)＝ －3.综上所述，△DBC的面积S取值范围为 －3≤S≤3＋ .
3. (2023龙东地区)如图，在Rt△ACB中，∠BAC＝30°，CB＝2，点E是斜边AB的中点，把Rt△ABC绕点A顺时针旋转，得Rt△AFD，点C，点B旋转后的对应点分别是点D，点F，连接CF，EF，CE，在旋转的过程中．△CEF面积的最大值是__________．
4. 如图，在矩形ABCD中，cs ∠DAC＝ ，BC＝3，E是AB的中点，将BE绕着点B逆时针旋转，在旋转的过程中，点E的对应点为点F，连接AF，CF，当△ACF的面积最小时，AF的长是________．
由题干可得出点F的运动轨迹，当△ACF的面积最小时，则点F到AC的距离最短，结合辅助圆求解即可．
5. 如图，在边长为4的正方形ABCD中，将△ABD沿射线BD平移，得到△EGF，连接EC，GC，DE，当G为BD的中点时，DE的长为________，在平移的过程中，EC＋GC的最小值为________．
6. (2019成都B卷24题4分)如图，在边长为1的菱形ABCD中，∠ABC＝60°，将△ABD沿射线BD的方向平移得到△A′B′D′，分别连接A′C，A′D，B′C，则A′C＋B′C的最小值为________．
【解析】如解图，设A′C交BD于点O，连接AO，AC，延长DA到点E，使得AE＝AD，连接B′E，CE.
由平移性质可知，A′B′∥CD且A′B′＝CD，∴四边形A′B′CD是平行四边形，∴B′O＝OD，A′O＝OC，
由菱形性质可知，A，C关于BD对称，∴AO＝OC＝OA′.∵AD＝EA，OD＝OB′，∴AO是△DEB′的中位线，∴B′E∥AO且B′E＝2AO＝A′C，∴A′C＝B′E，∴当点B′在CE上时A′C＋B′C最小，最小值为CE.在△DCE中，∵AE＝AC，∠EAC＝180°－∠DAC＝120°，∴∠AEC＝∠ACE＝30°，∴∠ECD＝∠ACE＋∠ACD＝90°，
∵ED＝2AD＝2，CD＝1，∴EC＝ ，即A′C＋B′C的最小值为 .
7. 定义：有一组邻边相等的凸四边形叫做等邻边四边形．如图，在Rt△ABC中，∠ABC＝90°，AB＝2，BC＝1，将△ABC沿∠ABC的平分线BB′的方向平移，得到A′B′C′，连接AC′，CC′，若四边形ABCC′是等邻边四边形，则平移距离BB′的长度是________．
8. (2023锦江区模拟)如图，正方形ABCD的边长为2，E是边AB上的动点，连接ED，EC，将ED绕点E顺时针旋转90°得到EN，将EC绕点E逆时针旋转90°得到EM，连接MN，则线段MN的取值范围为_____________．
由线段ED，EC分别旋转90°，且四边形ABCD为正方形，可知题干中隐含“一线三等角”模型.