湖北省武汉市汉阳区2023-2024学年八年级上学期期中考试数学试卷(含答案)

这是一份湖北省武汉市汉阳区2023-2024学年八年级上学期期中考试数学试卷(含答案)，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（每小题3分，共30分）
下列各题中有且只有一个正确答案，请在答题卡上将正确答案的标号涂黑.
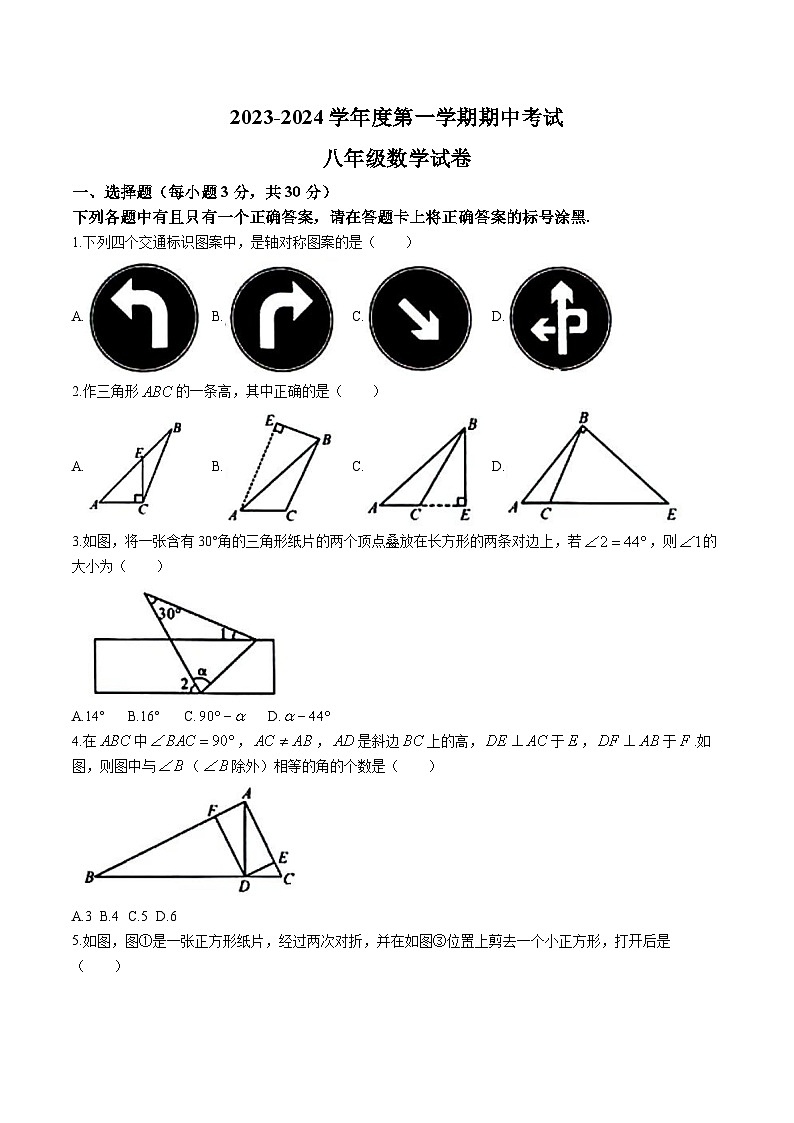
1.下列四个交通标识图案中，是轴对称图案的是（ ）
A.B.C.D.
2.作三角形的一条高，其中正确的是（ ）
A.B.C.D.
3.如图，将一张含有30°角的三角形纸片的两个顶点叠放在长方形的两条对边上，若，则的大小为（ ）
A.14°B.16°C.D.
4.在中，，是斜边上的高，于，于.如图，则图中与（除外）相等的角的个数是（ ）
A.3B.4C.5D.6
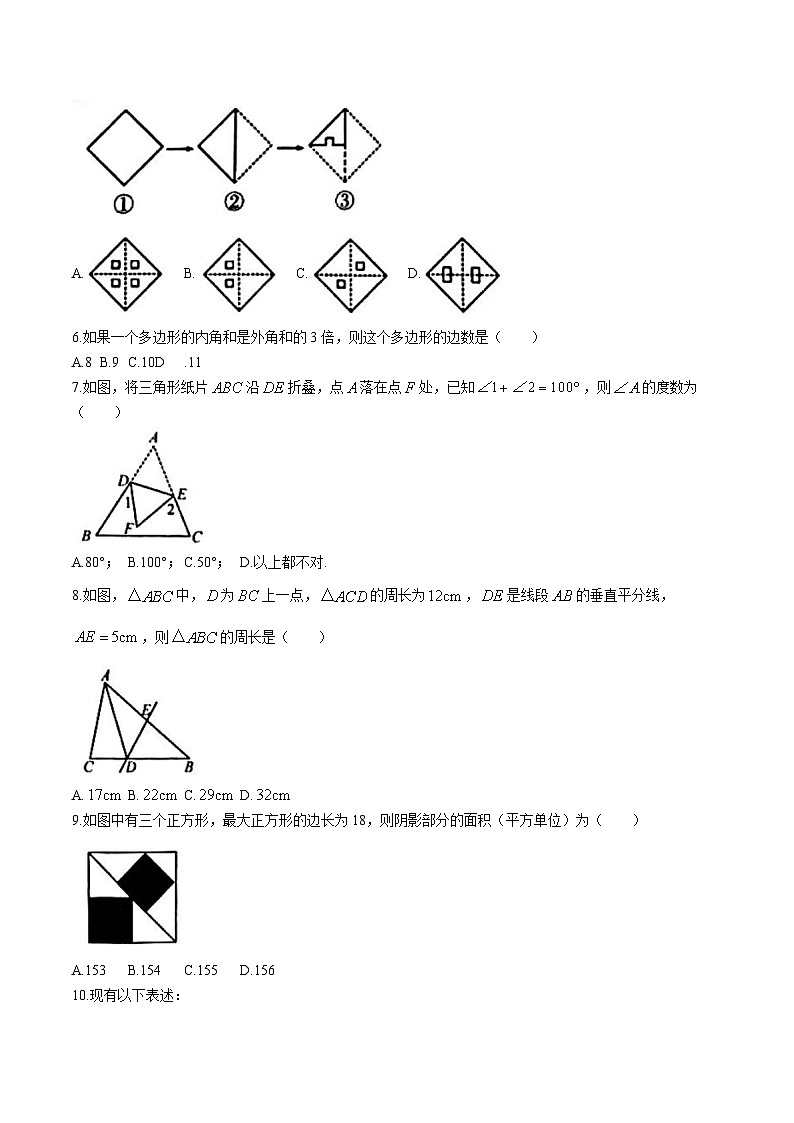
5.如图，图①是一张正方形纸片，经过两次对折，并在如图③位置上剪去一个小正方形，打开后是（ ）
A.B.C.D.
6.如果一个多边形的内角和是外角和的3倍，则这个多边形的边数是（ ）
A.8B.9C.10D.11
7.如图，将三角形纸片沿折叠，点落在点处，已知，则的度数为（ ）
A.80°；B.100°；C.50°；D.以上都不对.
8.如图，中，为上一点，的周长为，是线段的垂直平分线，，则的周长是（ ）
A.B.C.D.
9.如图中有三个正方形，最大正方形的边长为18，则阴影部分的面积（平方单位）为（ ）
A.153B.154C.155D.156
10.现有以下表述：
①三角形按边相等关系分类有三边都不等的三角形、等腰三角形和等边三角形；
②三角形的三边中线一定交于一点，三角形的高也一定交于一点；
③平面上有四个点、、、，用它们作顶点可以构成3个或4个三角形；
④有8根木棒，长度分别为1、2、3、4、5、6、7、8，其中最长边是8，另两边的差大于2，这样的三角形可以有4种.其中正确的个数为（ ）
A.1；B.2；C.3；D.4
二、填空题（共6小题，每小题3分，共18分）
下列各题不需要写出解答过程，请直接填写在答题卡指定的位置.
11.点关于轴对称的点坐标为_________.
12.已知，，是的三边长，，满足，为奇数，则_________.
13.如图，在五边形中，，、分别平分、，则的度数为_________.
14.如图，中，，，，，，则________.
15.如图，在凸四边形中，，.现有以下结论：
①若为中点，连，过作的垂线交于点，连，如图15-1，则有；
图15-1
②当点为凸四边形的一个动点，有最大值时，线段一定过的中点；
③当点为凸四边形的一个动点，则的面积为；
④.
其中正确的结论有________________.
16.如图是一个的小正方形拼成的大正方形，则图中的度数和是_________.
三、解答题（共8小题，共72分）
下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形.
17.（本小题满分8分）
如图，在中，，中线将这个三角形的周长分成15和12两部分，求这个三角形三边的长.
18.（本题满分8分）
如图，，于，于，若，求证：（1）；（2）.
19.（本题满分8分）
一个凸多边形的内角和比它的外角和的3倍少180°，求这个多边形的边数.
20.（本题满分8分）
将的正方形棋盘沿格线划分成两个全等图形，约定某种划分法经过旋转、轴对称得到划分方法与原划分法相同.如图1与图2的涂色方式.请你按照这种划分方法，在备用图中涂色来表示划分办法.
21.（本题满分8分）
如图，在平面直角坐标系中，，，.
（1）在图中作出关于直线（直线上各点的横坐标都为1）对称的图形；
（2）线段上有一点，直接写出点关于直线对称的点的坐标；
（3）线段上有一点，直接写出点关于直线对称时与满足的数量关系；
（4）若直线交轴于点，直接写出点坐标.
22.（本题满分10分）
已知，在中，，，为直线上一点.
（1）如图，在线段上，连，过作于点，交于点，若平分，则求证：；
（2）当点在直线上移动时，连，过作的垂线，垂足为，连，直接写出的度数.
23.（本题满分10分）
问题的提出：如图1，中，，则求证：.
知识的运用：如图3，四边形是正方形，，，点是边上一点，，且，连.求的度数.
拓展与延伸：如图4，四边形中，，，，为四边形边上一点，连，若，且，探究与的数量关系.直接写出结果，不需说明理由.
24.（本题满分12分）
数学问题：如图1，的中线、交于点，试探究线段与间的数量关系，并说明理由.
数学思考：如图2，的中线、交于点，连，
（1）求证：；
（2）求证：.
数学运用：
①如图3，在四边形中，，，、分别是、边的中点，直接写出、与间的数量关系，不需要说明理由.
②如图4，现有一块四边形纸片，，，、分别为、中点，，、也同时是、的中点.现若有，，或点到的距离为，请直接写出四边形的面积（用、、表示）.
数学答案
一、选择题
二、填空题
三、解答题：
17.解：为中线，
，
，
，…………………………3分
设，，则依题意有：
时，；或时，.
时，；或时，.………………………………5分
，，；或，，.……………………7分
经验证，均满足条件，
所以这个三角形的三边的长分别为：10、10、7或8、8、11.……………………8分.
18.证明：（1）于，于，
，……………………2分
，
，
，……………………4分
在与中，
，……………………1分
.
.…………………………8分
19.解：设这个多边形的边数为，依题意有：
…………………………4分
解得：.…………………………7分
答：这个多边形的边数为7.……………………8分
20.略
21.（1）
（2）；
（3）；
（4）
22.（1）证明；平分，
，
于，
，
，
，
，
，
在上取点，使，连，如图.
在与中，
，…………………………3分
.
.
.
在与中，
，…………………………6分
.
…………………………7分
（2）45°或135°.……………………10分.
23.问题的提出：
证明：取中点，连，
，
在和中，
，
.……………………3分
其他如作，或作的角平分线交于点，对照给分.
特别的，只写，，只给1分.
知识的运用：
证明：，
，
，
，
在上取一点，使，连，如图.
，
，，
由问题的提出知：.…………………………5分
，
，
.
在和中，
，
……………………7分.
拓展与延伸：…………………………10分.
24.数学问题：
解：，理由如下：……………………1分
延长到，使，连，如图.
为中线，
.
在和中，
，.
.
延长到，使，如图，
同理可证：，.
，.
.
在和中，
，…………………………4分
数学思考；
证明：延长到，使，连，如图.
为中线，
.
在和中，
，
，.
.
.
是中线，
，
.
在和中，
，.
，
.…………………………8分
数学运用：①；…………………………10分
②.……………………12分.题号
1
2
3
4
5
6
7
8
9
10
答案
C
C
A
A
D
A
C
B
A
A
题号
11
12
13
14
15
16
参考答案
7
60°
①②③
405°