人教版八年级数学下册基础知识专题17.3 勾股定理（分层练习）（提升练）

这是一份人教版八年级数学下册基础知识专题17.3 勾股定理（分层练习）（提升练），共28页。
A． B． C． D．
2．（2024上·山西晋中·八年级统考期末）公园有一块长方形草坪，芳芳同学发现有极少数人为了走捷径，践踏草坪走出了一条路，为了倡导人们爱护花草，建议公园管理人员在处立一个标牌：“小草青青，脚下留情” ．经过测量得知：两处的距离为两处的距离为则践踏草坪少走的距离是（ ）
A． B． C． D．
3．（2023下·重庆铜梁·八年级重庆市巴川中学校校考期末）如图，露在水面上的鱼线长为．钓鱼者想看看鱼钩上的情况把鱼竿提起到的位置，此时露在水面上的鱼线长为4m，若的长为，试问的鱼竿有多长？设长，则下所列方程正确的是（ ）.
A． B．
C． D．
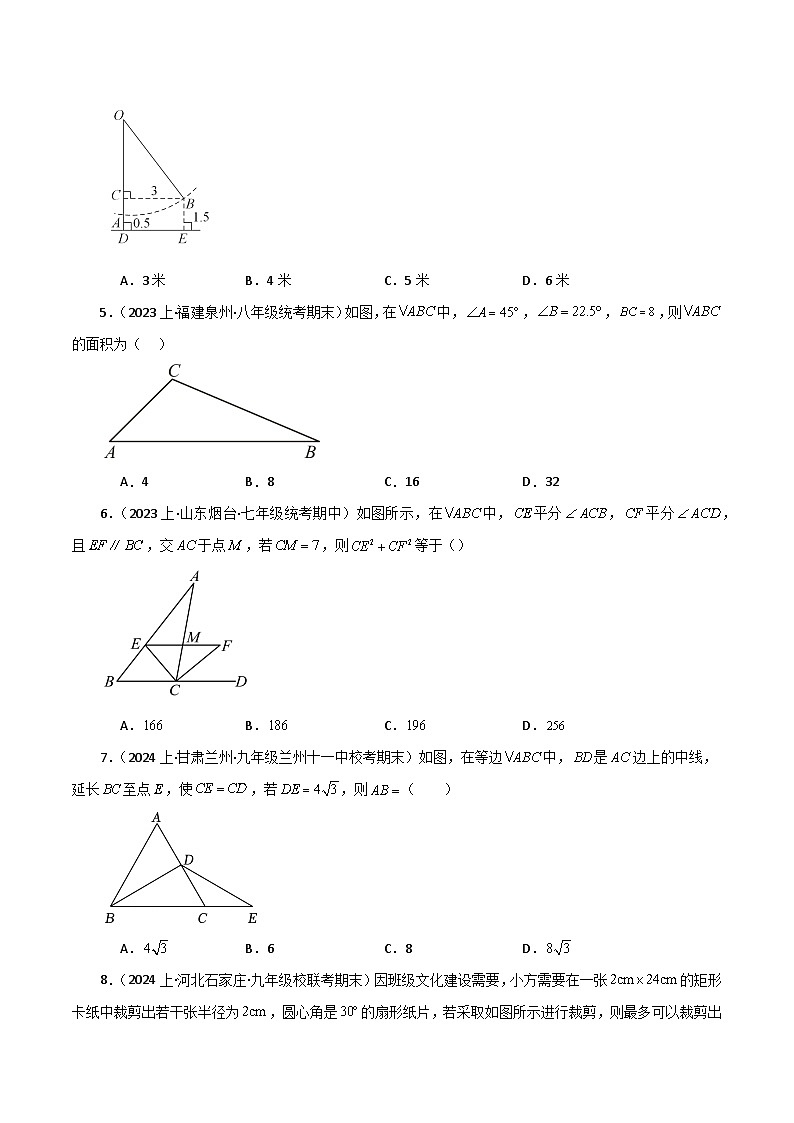
4．（2022下·北京海淀·八年级统考期末）如图，有一架秋千，当它静止时，踏板离地0.5米，将它往前推3米时，踏板离地1.5米，此时秋千的绳索是拉直的，则秋千的长度是（ ）
A．3米 B．4米 C．5米 D．6米
5．（2023上·福建泉州·八年级统考期末）如图，在中，，，，则的面积为（ ）

A．4 B．8 C．16 D．32
6．（2023上·山东烟台·七年级统考期中）如图所示，在中，平分，平分，且，交于点，若，则等于（）
A． B． C． D．
7．（2024上·甘肃兰州·九年级兰州十一中校考期末）如图，在等边中，是边上的中线，延长至点，使，若，则（ ）
A． B．6 C．8 D．
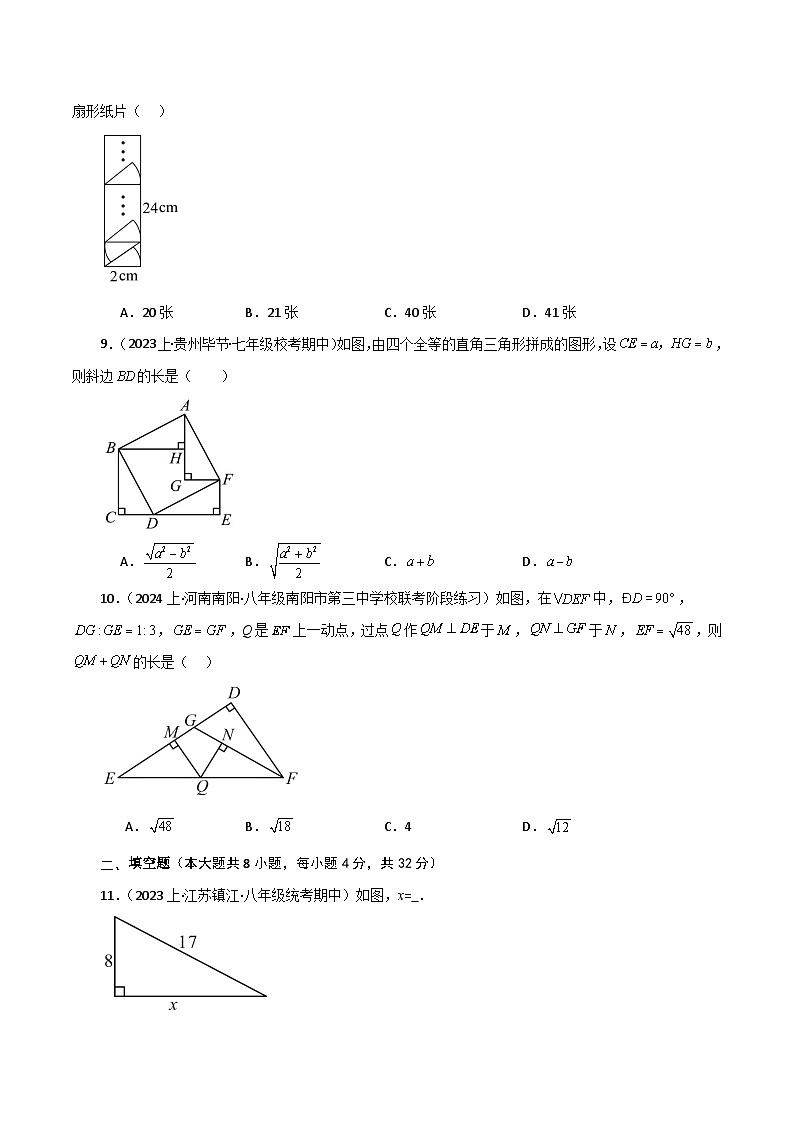
8．（2024上·河北石家庄·九年级校联考期末）因班级文化建设需要，小方需要在一张的矩形卡纸中裁剪出若干张半径为，圆心角是的扇形纸片，若采取如图所示进行裁剪，则最多可以裁剪出扇形纸片（ ）

A．20张 B．21张 C．40张 D．41张
9．（2023上·贵州毕节·七年级校考期中）如图，由四个全等的直角三角形拼成的图形，设，则斜边的长是（ ）
A． B． C． D．
10．（2024上·河南南阳·八年级南阳市第三中学校联考阶段练习）如图，在中，，，，Q是上一动点，过点作于，于，，则的长是（ ）
A． B． C．4 D．
填空题（本大题共8小题，每小题4分，共32分）
11．（2023上·江苏镇江·八年级统考期中）如图，x= ．
12．（2024上·四川成都·九年级四川省成都市玉林中学校考期末）如图，在射线上取，在射线上取，连接，以点为圆心，为半径画弧，交于点，以为圆心，为半径画弧，交于点，则 ．
13．（2023上·河南郑州·八年级校考期末）图中的两个滑块A，B由一个连杆连接，分别可以在垂直和水平的滑道上滑动．开始时，滑块A距O点20厘米，滑块B距O点15厘米．问：当滑块A向下滑13厘米时，滑块B滑动了 厘米．

14．（2023上·江苏南京·八年级校联考期末）如图，，，以 A点为圆心，长为半径作圆弧与数轴交于点P．若点A表示的数为0，点B表示的数为1，则点P表示的数为 ．
15．（2023·安徽·模拟预测）如图，四边形的对角线相交于点，过点作于点，与交于点．请完成下列问题：

（1） ；
（2）若，则的长为 ．
16．（2024上·陕西咸阳·八年级统考期末）如图，圆柱形玻璃杯高为，底面周长为，在杯内离杯底的点处有滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿与蜂蜜相对的点处．则蚂蚁到达蜂蜜点的最短距离为 ．
17．（2024上·四川成都·八年级统考期末）在平面直角坐标系中，给出如下定义：对于以为底边的等腰及外一点C，若，直线中，其中一条经过点O，另一条与的腰垂直，则称点C是的“关联点”．如图，已知点，，，则点就是的“关联点”．若点是的“关联点”，则线段的长是 ．

18．（2024上·浙江衢州·八年级统考期末）在直角三角形纸片中，，折叠纸片使得点落在边上点处，折痕是（如图1），将纸片复原，再次折叠纸片，使得点落在边上的点处，折痕是（如图2），继续折叠纸片，使得点与点重合，折痕是，得到多边形（如图3），将若干个全等的多边形交叉重叠便可得到棒棒糖的糖果部分（如图4）．

（1）图1中的长为 ．
（2）图3中的长为 ．
三、解答题（本大题共6小题，共58分）
19．（8分）（2024上·福建厦门·八年级统考期末）如图，在中，，，，点C和点D关于直线对称．
（1）求作点D；（要求：尺规作图，保留作图痕迹，不写过程）
（2）连接，过点C作交的延长线于点E，求的长度．
20．（8分）（2023上·辽宁朝阳·八年级统考期末）如图，在平面直角坐标系中，长方形的顶点A、C的坐标分别是和，E为C点左侧x轴上一动点，连接，将沿所在直线翻折得到，当点恰好落在y轴上时，求的长（提示：点E可能在x轴正半轴上，也可能在x轴负半轴上）
21．（10分）（2024上·福建福州·八年级福建师大附中校考期末）如图，中，，点在的边上，，以为直角边在同侧作等腰，使，过作于点，连接．
（1）求证：；
（2）当时，则为多少；
（3）若，求的值．
22．（10分）（2023上·辽宁丹东·八年级统考期中）如图，有一架救火飞机沿东西方向，由点飞向点，在直线的正下方有一个着火点，且点与两点的距离分别为和，又两点距离为，飞机与着火点距离在以内可以受到洒水影响．
（1）请通过计算说明，着火点是否受洒水影响；
（2）若救火飞机的速度为，要想扑灭着火点估计需要13秒，请你通过计算说明在救火飞机从点飞到点的过程中，着火点能否被扑灭．
23．（10分）（2024上·江苏南京·八年级校联考期末）在中，，
（1）如图①，为边上一点，连接，以为边作，，，连接．求证：，
（2）如图②，为外一点．若，，．则的长为______．
24．（12分）（2024上·陕西汉中·八年级统考期末）【问题提出】
（1）如图1，为的边上的高，若，，则的长为________；
【问题探究】
（2）如图2，在中，，平分交于点D，若，，求的长；
【问题解决】
（3）如图3，直线l是一条小路，是李叔叔家的一块花园的平面示意图，其中边在小路l上，边上的点D处有一口灌溉水井，经测量，，米，米．李叔叔计划对该花园进行扩建，在点C右侧的小路l上取点E，并在、、内分别种植不同的花卉，根据李叔叔的规划要求，，请你计算区域的面积．
参考答案：
1．A
【分析】本题考查了等腰直角三角形的性质及勾股定理，根据等腰直角三角形的性质及勾股定理得该等腰直角三角形的直角边为，再利用三角形的面积公式即可求解，熟练掌握基础知识是解题的关键．
解：依题意得：
该等腰直角三角形的直角边为：，
面积为：，
故选A．
2．D
【分析】本题考查了勾股定理．熟练掌握勾股定理是解题的关键．
由勾股定理得，，根据，计算求解即可．
解：由题意知，，
由勾股定理得，，
∵，
∴则践踏草坪少走的距离为，
故选：D．
3．A
【分析】如图：设长，则，分别在和可得、，再根据可得，然后代入相关数据即可解答．
解：设长，则，
在中，，
在中，，
∵，
∴，即．
故选A．
【点拨】本题主要考查了勾股定理的应用，掌握勾股定理的基本形式以及的隐含条件是解答本题的关键.
4．C
【分析】设米，用表示出的长，在直角三角形中，利用勾股定理列出关于的方程，求出方程的解即可得到结果．
解：设米，
米，米，
（米，米，
在中，米，米，米，
根据勾股定理得：，
解得：，
则秋千的长度是5米．
故选：C．
【点拨】此题考查了勾股定理的应用，熟练掌握勾股定理是解本题的关键．
5．C
【分析】本题主要考查了勾股定理，等腰直角三角形的性质与判定，过点C作于D，交于E，先证明，设，则，再证明，得到，则，利用勾股定理得到，解得，则．
解：如图所示，过点C作于D，交于E，
∴，
∵，
∴，
∴，
∴，
设，
∴，
∵，，
∴，
∴，
∴，
∵，
∴，
∴，
∴，
∴
，
故选：C．

6．C
【分析】本题考查了等腰三角形的判定与性质，勾股定理，熟练掌握勾股定理是解题的关键． 根据角平分线的定义和平行线的性质可得和是等腰三角形，可得，从而可得，然后再利用角平分线的定义以及平角定义可得，从而在中，利用勾股定理进行计算，即可解答．
解：平分平分，
在中，
故选：C．
7．C
【分析】此题主要考查了等边三角形的性质，等腰三角形的判定和性质，勾股定理等．先由等边三角形的性质，得，，，再根据，得，进而得，则，然后在中，由勾股定理求出即可．
解：为等边三角形，
，，
是边上的中线，
，，，
，
，
，
，
，
，
，
，
在中，由勾股定理得：，
即，
解得：，
．
故选：C．
8．C
【分析】本题主要考查了含30度角的直角三角形的性质，二次根式除法，在中，，则，再由即可得到答案．
解：如图所示，在中，，
∴，
∵，
∴最多可以裁剪出扇形纸张，
故选：C．

9．B
【分析】本题考查了勾股定理，全等三角形的性质，用含a，b的式子表示各个线段是解题的关键．解：设，则，求得，求得 ，得到，根据勾股定理即可得到结论．
解：设，则，
∵，
∴，
∴，
∴，
∴，
∴，
故选：B．
10．C
【分析】本题考查了勾股定理及等面积法，连接，设，通过勾股定理得出ｋ的值，再求出，再利用等面积法求解即可，熟练掌握知识点是解题的关键．
解：连接，
∵，
∴设，
∴，
∵，
∴，
∵，
∴，
∴，
∵，
∴，
解得（负舍），
∴，
∴，
∵，
∴，
∴，
故选：C．
11．15
【分析】本题考查了直角三角形三边之间的关系，根据勾股定理可求得的值，正确计算是解答本题的关键．
解：∵三角形是直角三角形，
∴，
解得：，
故答案为：．
12．
【分析】本题考查作图-基本作图、勾股定理，解题的关键是理解题意，灵活运用所学知识解决问题．由题意得，，，由勾股定理得，则，，即可得出答案．
解：由题意得，，，，
，
，
．
故答案为：．
13．9
【分析】根据勾股定理求出的长，再求出下滑后的，利用勾股定理求出下滑后的，继而求出滑块B滑动的距离．
解：依题意得：，
设滑动后点A、B的对应位置是，
由勾股定理得，（厘米），
当滑块A向下滑13厘米时，（厘米），
∴（厘米），
∴滑块B滑动的距离为：（厘米），
故答案为：9．
【点拨】本题考查的是勾股定理的应用，善于观察题目的信息，灵活运用勾股定理是解题的关键．
14．
【分析】利用勾股定理求出，则可得，再利用实数与数轴关系即可得出答案．
解：点A表示的数为0，点B表示的数为1，
∴，
∵，
∴由勾股定理，得
，
，
∴，
∵点P在数轴的负半轴上，
∴点P表示的数为．
故答案为：．
【点拨】本题考查勾股定理，实数与数轴，熟练掌握勾股定理和用数轴上的点表示实数是解题的关键．
15． 45
【分析】本题考查了等腰三角形的性质，勾股定理，线段垂直平分线的性质等知识．
（1）设，由等腰三角形的性质可得，，再根据三角形外角的性质求解即可；
（2）连接，则易得，；由勾股定理求出，再由等腰三角形性质及勾股定理求得，即可得结果．
（1）解：设，
，，
．
，，
∴，
．
（2）解：如图，连接．

∵，
∴；
∵，
∴，
∴；
，
；
，，
由勾股定理得：，
．
16．10
【分析】本题考查了平面展开-最短路径问题，将图形展开，利用轴对称的性质和勾股定理进行计算是解题的关键，将杯子侧面展开，建立A关于的对称点，根据两点之间线段最短可知的长度即为所求．
解：如图，将杯子侧面展开，作关于的对称点，连接，则即为最短距离，
圆柱形玻璃杯底面周长为，杯底的点处，沿与蜂蜜相对的点处，
，，，
，
故答案为：10．
17．/
【分析】此题考查了勾股定理，过点Q作轴于点A，利用勾股定理求出，利用面积法求出的长，勾股定理求出，得到，再根据勾股定理求出线段的长．
解：如图，过点Q作轴于点A，

∵是的“关联点”， ，，
∴，
∴，
∵，
∴，
∴，
∴，
∴．
故答案为．
18． 3
【分析】本题考查了勾股定理与折叠问题，等腰三角形的性质与判定，全等三角形的性质与判定；
（1）在直角三角形纸片中，，勾股定理求得，如图1中，设，则，，在中，勾股定理即可求解；
（2）设交于点，根据折叠可得，证明，在中，勾股定理求得，进而证明，即可求解．
解：（1）在直角三角形纸片中，，
∴，
如图1中，设，则，，
根据折叠可得，，
在中，，
即，
解得：，
∴，
故答案为：．
（2）∵折叠，
∴，，
∴；
在图2中，设交于点，根据折叠可得，

∴，
又∵，
∴，
∴，
∴；
∴设，则，
在中，，
∴，
解得：，
∴；
在图3中，∵，
∴，
∴；
在中，，
∴，
∴，
∴，
∴；
∵，
∴；
故答案为：．
19．（1）见分析；（2）6
【分析】本题考查了作图，平行线的性质和判定，轴对称的性质，勾股定理，熟练掌握基本作图以及平行线的性质是解题的关键
（1）在的上方作，在射线上截取，使，点D即为所求；
（2）过 A 作 于 H，设交直线于 G，分别求出，可得结论
解：（1）如图所示
（2）过 A 作 于 H，设交直线于 G，
，，
，，
由，
，
解得 ， ，
点C和点D关于直线对称，
，
，
，
，
，
是线段的垂直平分线，
在中，，，
，
，
20．或
【分析】本题考查坐标与轴对称，勾股定理．分点在轴正半轴上和点在轴负半轴上，两种情况，进行求解即可．解题的关键是画出图形，利用数形结合和分类讨论的思想进行求解．
解：当点在轴正半轴上时，如图：设交轴于点，则：四边形均为长方形，
∵长方形的顶点A、C的坐标分别是和，
∴，，，
∵翻折，
∴，，
在中，，
∴，
设，则，
在中，，
即：，
∴，即：；
当点在轴负半轴上时：如图
同法可得，
∴，
设，则，
在中，，
即：，
∴，即：，
综上：或．
21．（1）见分析；（2）2；（3）
【分析】（1）首先证得，利用全等三角形的判定定理即可得解；
（2）利用全等三角形的性质可得，可得，由勾股定理可得，进一步计算可得结果；
（3）由（1）得，可得，利用勾股定理得到，可得，进一步计算可得结果；
解：（1）证明：∵，
∴，
∵，，
∴，
又∵是等腰直角三角形，
∴，
在和中，
∴；
（2）解：由（1）得，
∴，
∴，
由勾股定理得，，
∵，
∴，
解得；
（3）解：由（1）得，，
，
整理得，即，
∴，
∵，
∴，
∴，
∴，
在中，由勾股定理得，
，
∴，
∴，
∴，
，解得，
即．
【点拨】本题主要考查了等腰直角三角形的性质，勾股定理和全等三角形的性质与判定，结合勾股定理计算是解题的的关键．
22．（1）着火点洒水影响，见分析；（2）着火点能被扑灭，见分析
【分析】本题考查了勾股定理与勾股定理的逆定理的应用，等腰三角形的性质，
（1）过点作，垂足为，勾股定理的逆定理证明是直角三角形，进而等面积法求得长度，与500进行比较即可求得答案；
（2）以点为圆心，为半径作圆，交于点，勾股定理求得，进而求得的长，根据飞机的速度得到飞行时间，再根据题意求得灭火时间，即可解决问题．
（1）解：着火点C受洒水影响，理由如下，
如图，过点作，垂足为，

，，，
，，
，
是直角三角形，
，
（米），
，
着火点C受洒水影响
（2）解：如图，当时，飞机正好喷到着火点，

，
，
在中，，
，
飞机的速度为，
（秒），
14秒13秒，
着火点能被扑灭，
答：着火点能被扑灭．
23．（1）见分析；（2）
【分析】本题考查了全等三角形的性质与判定，勾股定理，等腰三角形的性质；
（1）先证明可得，进而可得，再证明，即可得出结论；
（2）根据（1）的方法，以为边作，，，证明，根据已知条件得出是等腰直角三角形，，中，勾股定理求得，进而根据，即可求解．
解：（1）证明：∵
即
在和
∴
即；
（2）解：如图所示，以为边作，，，
同（1）可得，
∴，，
∴是等腰直角三角形，
∴，，
∴
在中，
∴
∴，
故答案为：．
24．（1）1；（2）12；（3）区域的面积为2100平方米
【分析】本题考查了勾股定理的应用，全等三角形的判定和性质，角平分线的性质：
（1）根据勾股定理求得，再由，即可得到答案；
（2）过点D作于点E，由角平分线的性质可得，，再根据勾股定理求得，再证明，可得，再利用勾股定理建立方程求解即可；
（3）过点D作于点F，由可知平分，则，由勾股定理求得，再证明，再利用勾股定理建立方程求得，进而求得，再利用三角形的面积公式求解即可．
（1）解：，，
在中，，
，
，
故答案为：1；
（2）解：过点D作于点E，如图．
平分，
，，
．
，，，
，
．
设，则，．
在中，，
，
解得，即的长为12．
（3）解：过点D作于点F，如图3．
，
平分，
米，
（米）．
，，，
，
．
设米，则米，米．
在中，，
，解得，
（米），
（平方米）．
即区域的面积为2100平方米．