



初中数学沪科版九年级上册23.2解直角三角形及其应用图片ppt课件
展开比较熟练的应用解直角三角形的知识解决与仰角、俯角有关的实际问题.
应用解直角三角形的知识解决与仰角、俯角有关的实际问题.
选用恰当的直角三角形,解题思路分析.
1.什么是解直角三角形?
2.在下列所给的直角三角形中,不能求出解的是( )A.已知一直角边和所对的锐角 B.已知一直角和斜边C.已知两直角边 D.已知斜边和一锐角
答:在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形.
某探险者某天到达如图所示的点A 处时,他准备估算出离他的目的地,海拔为3500 m的山峰顶点B处的水平距离.
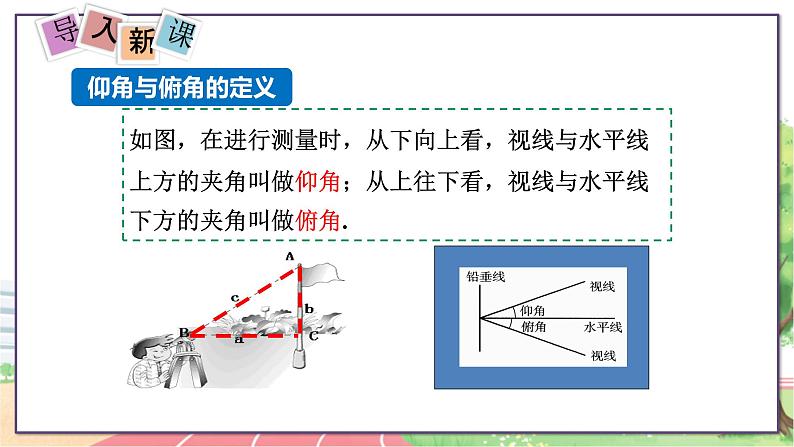
如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
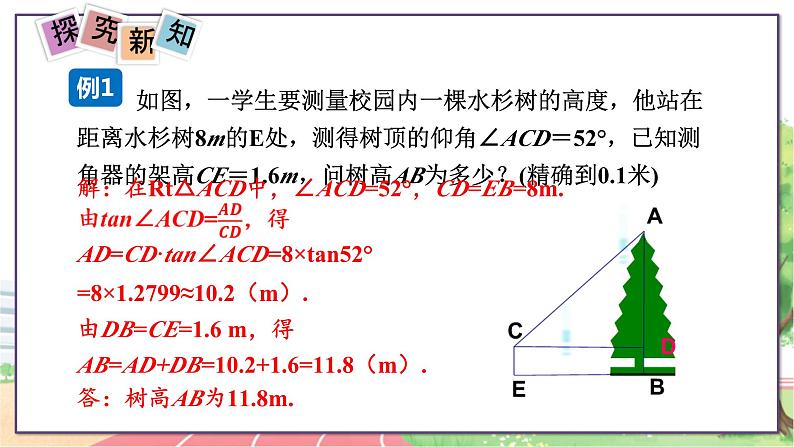
如图,一学生要测量校园内一棵水杉树的高度,他站在距离水杉树8m的E处,测得树顶的仰角∠ACD=52°,已知测角器的架高CE=1.6m,问树高AB为多少?(精确到0.1米)
答:树高AB为11.8m.
解:在Rt△ACD中,∠ACD=52°,CD=EB=8m.
AD=CD·tan∠ACD=8×tan52°
=8×1.2799≈10.2(m).
由DB=CE=1.6 m,得
AB=AD+DB=10.2+1.6=11.8(m).
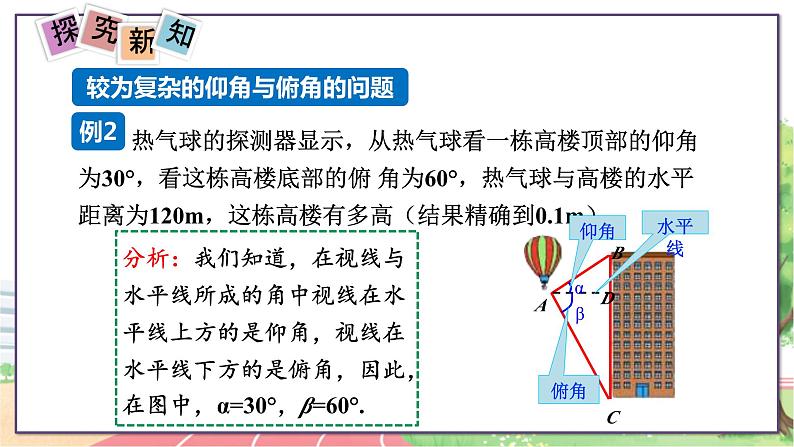
热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯 角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α=30°,β=60°.
较为复杂的仰角与俯角的问题
由分析可知α=30°,β=60° Rt△ABD中,a =30°,AD=120,所以利用解直角三角形的知识求出BD的长度;类似地可以求出CD的长度,进而求出BC的长度,即求出这栋楼的高度.
解:如图,α = 30°,β= 60°,AD=120.
答:这栋楼高约为277.1m.
∴BD=AD·tanα=120×tan30°
∴CD=AD·tanβ=120×tan60°
广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲乙二人分别站在E、F处,他们看气球的仰角分别是30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.5米,请问此气球有多高?(结果保留到0.1米)
∴BF=PB=(h+1)米
∴EA=BF+CD=h+1+5
在Rt△PEA中,PA=AE·tan30°
∴h=(h+6)tan30°
如图,某校九年级学生要测量当地电视塔的高度AB,因为不能直接到达塔底B处,他们采用在发射台院外与电视塔底B成一直线的C,D两处地面上,用测角器测得电视塔顶部A的仰角分别为45°和30°,同时量得CD为50 m.已知测角器高为1 m,问电视塔的高度为多少米?(精确到1 m)
在Rt△AC1B1中,
在Rt△AD1B1中,
∴AB=AB1+B1B,
答:电视塔的高度为69m
由∠AC1B1=45°,
由∠AD1B1=30°,
1. 如图①,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=_______米.
2. 如图②,两建筑物AB和CD的水平距离为30米,从A点测得 D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为________米.
∴CD=BCsin60°
4. 建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).
解:在等腰Rt△BCD中,∠ACD=90°,BC=DC=40m.
∴AC=tan∠ADC·DC
tan54°×40≈1.38×40=55.2(m),
∴AB=AC-BC=55.2-40=15.2(m)
所以,楼房CD的高度约为32.4米.
解:作BE⊥CD于点E,
∴CD=CE+DE=12+12 ≈32.4,
6. 如图,直升飞机在长400米的跨江大桥AB的上方P点处,在大桥的两端测得飞机的仰角分别为37°和45°,求飞机的高度 .(结果取整数. 参考数据:sin37°≈0.8,cs37°≈0.6,tan 37°≈0.75)
在Rt△POB中,∠PBO=45°
在Rt△POA中,∠PAB=37°,
解:作PO⊥AB交AB的延长线于O.设PO=x米,
故飞机的高度为1200米.
仰角、俯角问题的常见基本模型:
初中数学华师大版九年级上册24.4 解直角三角形教学课件ppt: 这是一份初中数学华师大版九年级上册<a href="/sx/tb_c21366_t3/?tag_id=26" target="_blank">24.4 解直角三角形教学课件ppt</a>,共19页。PPT课件主要包含了知识要点,与夹角有关问题,新知导入,课程讲授,随堂练习,由题意可得,在Rt△ABD中,BD400米,在Rt△BCD中,∴CD400米等内容,欢迎下载使用。
初中数学华师大版九年级上册24.4 解直角三角形教学演示课件ppt: 这是一份初中数学华师大版九年级上册24.4 解直角三角形教学演示课件ppt,共11页。PPT课件主要包含了完成第2课时练习等内容,欢迎下载使用。
沪科版九年级上册23.2解直角三角形及其应用习题ppt课件: 这是一份沪科版九年级上册23.2解直角三角形及其应用习题ppt课件,共23页。













