2024年河北省中考数学模拟考试试题（含答案）

这是一份2024年河北省中考数学模拟考试试题（含答案），共14页。试卷主要包含了 单选题， 填空题， 解答题等内容，欢迎下载使用。

一、 单选题 （本题共计16小题，总分38分）
1.（3分）如图,将线段AB绕点A旋转,下列各点能够落到线段AB上的是( )
A.点CB.点DC.点ED.点F
2.（3分）如图,A,B,C、D四个点将数轴上-6与5两点间的线段五等分,这四个等分点位置最靠近原点的是( )
A.点AB.点BC.点CD.点D
3.（3分）下面括号内填入m4后,等式成立的是( )
A.()+m2=m6B.m3⋅()=m12C.()3=m7D.m12÷()=m8
4.（3分）如图,市政府准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的余弦值为45,则坡面AC的长度为( )
A.152mB.10mC.10mD.302m
5.（3分）某校足球队20名队员年龄分布情况如下表:
则该队队员年龄的众数、中位数分别是( )
A.15,13.5B.15,13C.13,13.5D.13,13
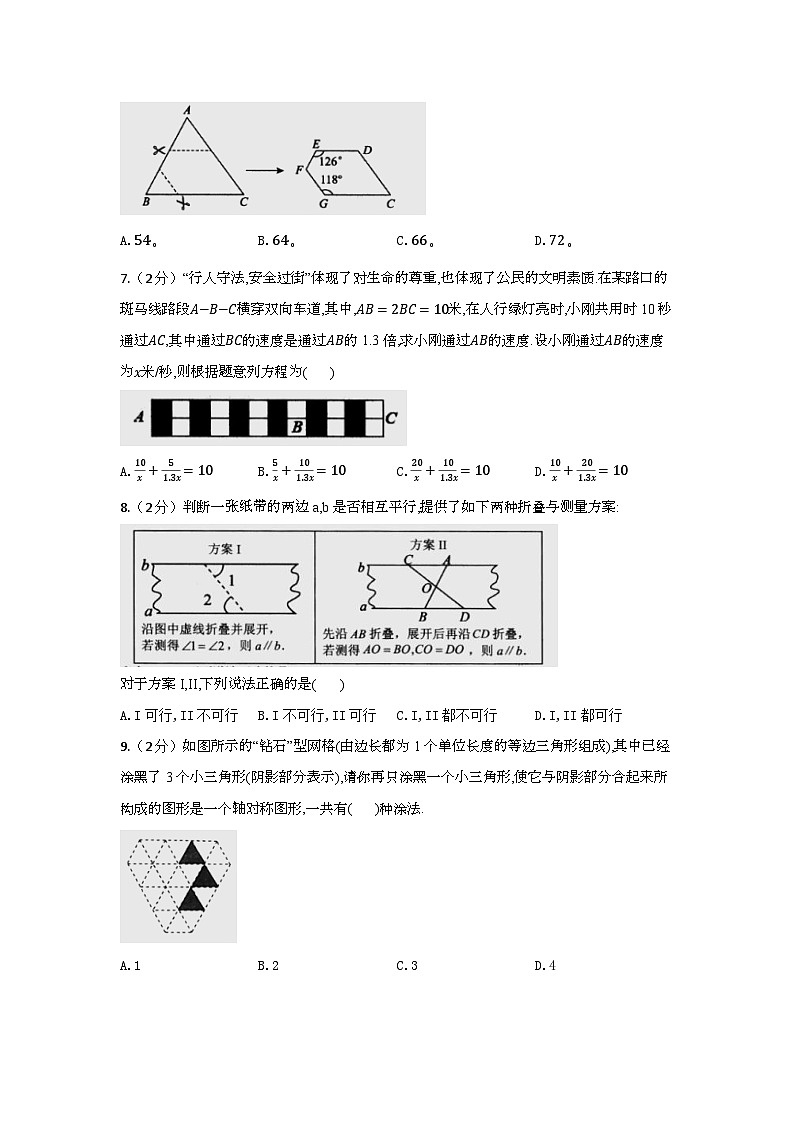
6.（3分）如图,将三角形纸片ABC沿虚线剪掉两角得五边形CDEFG,若DE//CG,FGHCD,根据所标数据,则∠A的度数为( )
A.54∘B.64∘C.66∘D.72∘
7.（2分）“行人守法,安全过街”体现了对生命的尊重,也体现了公民的文明素质.在某路口的斑马线路段A−B−C横穿双向车道,其中,AB=2BC=10米,在人行绿灯亮时,小刚共用时10秒通过AC,其中通过BC的速度是通过AB的1.3倍,求小刚通过AB的速度.设小刚通过AB的速度为x米/秒,则根据题意列方程为( )
A.10x+51.3x=10B.5x+101.3x=10C.20x+101.3x=10D.10x+201.3x=10
8.（2分）判断一张纸带的两边a,b是否相互平行,提供了如下两种折叠与测量方案:
对于方案I,II,下列说法正确的是( )
A.I可行,II不可行B.I不可行,II可行C.I,II都不可行D.I,II都可行
9.（2分）如图所示的“钻石”型网格(由边长都为1个单位长度的等边三角形组成),其中已经涂黑了3个小三角形(阴影部分表示),请你再只涂黑一个小三角形,使它与阴影部分合起来所构成的图形是一个轴对称图形,一共有( )种涂法.
A.1B.2C.3D.4
10.（2分）某地2024年3月份的旅游收入可以写成15×10n(n是整数)元,数据15×10n用科学记数法表示正确的是( )
A.2×10n−1B.2×10n+1C.5×10n−1D.5×10n+1
11.（2分）如图,锐角ΔABC中,∠B=45∘,要作ΔABC的高线CD，下列说法正确的是( )
A.只有甲对B.只有乙和丙对C.只有甲和丙对D.甲,乙,丙都对
12.（2分）“杠杆原理”在实际生产和生活中，有着广泛的运用.比如：小明用撬棍撬动一块大石头，运用的就是“杜杆原理”,即“阻力×阻力臂=动力×动力臂”.已知阻力F1(N)和阻力臂L1(m)的函数图象如图,若小明想用不超过150N的动力F2撬动这块大石头,则动力臂L2(单位:m)需满足( )
A.L2>4B.013.（2分）问题:“解方程−2x2+3x=8−x”,嘉嘉解得x1=1.5,x2=−2.5,淇淇看了嘉嘉的答案,说:“你算的不对,这个方程只有一个解.”判断下列结论正确的是( )
A.嘉嘉的解是正确的
B.淇淇说得对,因为b2−4ac=0
C.嘉嘉和淇淇的说法都不对,因为b2−4ac<0,该方程无解
D.由b2−4ac>0可得该方程有两个解,但嘉嘉的结果是错的
14.（2分）一个几何体的三视图如图所示,其中俯视图为正三角形,则该几何体的左视图中a的值为( )
A.2B.3C.1.7D.1.8
15.（2分）对于分式1−m21−m的值,下列说法一定正确的是( )
A.不可能为0B.比1大C.可能为2D.比m大
16.（2分）已知等边三角形ΔABC,边长为2,点P在BC边上,点P关于边AB,AC的对称点为M,N,线段MN的长范围为( )
A.22≤MN≤32B.2≤MN≤4C.3≤MN≤23D.3≤MN≤32
二、 填空题 （本题共计3小题，总分10分）
17.（2分）如图,“L”形图形的面积为7,如果a−b=1,那么a+b=_________
18.（4分）我市某中学举办剪纸艺术大赛,要求参赛作品的面积在20dm2以上.如图是小悦同学的参赛作品(单位:dm).
(1)小悦的作品________(填“是”或“否”)符合参赛标准;
(2)小涵给小悦提出建议:在参赛作品周围贴上金色彩条,这样参赛作品更漂亮,则需要彩条的长度约为_________dm(彩条的宽度忽略不计,结果保留一位小数,参考数据:2≈1.41).
19.（4分）如图,已知四个正六边形摆放在圆中,顶点A,B,C,D,E,F都在圆上,其中上下两个大一点的正六边形边长均为a,左右两个正六边形边长均为b.
(1)tan⁡∠ADE=_________；
(2)若b=3,则a=__________.
三、 解答题 （本题共计7小题，总分72分）
20.（9分）已知整式A=k−1,整式B=2k+3.如图,有一电脑AI程序,能处理整式的相关运算,若输入整式A,B后,屏幕上自动呈现整式C,但由于屏幕大小有限,只显示了整式C的一部分:C=2k2+.
(1)求程序自动呈现的整式C缺失的部分“”;
(2)嘉淇发现:若k取某个正整数时,整式B2−2C的值大于5,求满足条件的k的最小值.
21.（9分）小军与小玲共同发明了一种“字母棋”游戏来比胜负。他们把分别标有A,B,C,D字母的5枚相同的棋子装入一个不透明的袋子中,其中棋子A、C、D各1枚,棋子B有2枚.“字母棋”的游戏规则如下:①游戏时,两人各摸一枚棋子进行比赛称为一轮比赛,先摸者摸出的棋子不放回;②棋子A胜棋子B、C,棋子B胜棋子C、D,棋子C胜棋子D,棋子D胜棋子A；③相同棋子不分胜负.
(1)若小玲先摸,则小玲摸到棋子C的概率是_________
(2)若小玲先摸,小军后摸,画树状图或列表,求小玲摸到棋子B,且小玲胜小军的概率.
22.（9分）如图,某校的饮水机有温水、开水两个按钮,温水和开水共用一个出水口.利用图中信息解决下列问题:
(1)王老师拿空水杯先接了14s的温水,又接了8s的开水,刚好接满,且水杯中的水温为t∘C.
①王老师的水杯容量为_______ml;
②用含t的代数式表示接入水杯的温水吸收的热量,并用列方程的方法求t的值(不计热损失);
(2)嘉琪同学拿空水杯先接了一会儿温水,又接了一会儿开水,得到一杯210ml,温度为40∘C的水(不计热损失),求嘉琪同学的接水时间.
23.（10分）如图1,在正方形ABCD中,AB=25,O是边BC的中点,E是正方形内一动点,且OE=2,连接DE,将线段DE绕点D逆时针旋转90∘得DF,连接AE,CF
(1)求证：AE=CF
(2)求△CDF面积的最小值
(3)如图2，若A,E,O三点共线,求点F到直线BC的距离.
24.（10分）如图,直线l1:y=−43x+16与直线l2:y=kx+b交于点M(m,12),与x轴交于点P,直线l2经过点Q(−6,0),直线x=n分别交x轴、直线l1、l2于A,B,C三点.
(1)求m的值及直线l2的函数表达式;
(2)当点A在线段PQ上(不与点P,Q重合)时,若AB=2BC,求n的值;
(3)设点D(5,6)关于直线x=n的对称点为K,若点K在直线l1,直线l2与x轴所围成的三角形内部(包括边界),直接写出n的取值范围.
25.（12分）如图,点B为线段AC上一点,AC=5,AB=2,过B作BE⊥BC于B,且BE=4,以BC、BE为邻边作矩形BCDE,将线段AB绕点B顺时针旋转,得到线段BF,优弧AF^交BE于N,交BC于M,设旋转角为α
.
(1)若扇形MBF的面积为29π,则α=_________
(2)连接EC,判断CE与扇形ABF所在圆⨀B的位置关系,并说明理由;
(3)设P为直线AC上一点，沿EP所在直线折叠矩形，若折叠后DE所在的直线与扇形ABF所在的⨀B相切,直接写出CP的长.
26.（13分）嘉淇设计了一个程序,如图,拋物线L:y=x2−2px+p2+2p−3为导电的线缆,第一象限内有一矩形ABCD区域,边AD,DC分别在y轴,x轴上,点B的坐标为(8,6),其中矩形的顶点A,B,C,D处有四个通电开关.
(1)点A的坐标__________;
(2)当p=−4时,求拋物线L的对称轴和y的最小值;
(3)设抛物线L的顶点为点E.
①求点E的坐标(用含p的式子表示);
②当点E在矩形ABCD的边上时,求点E的坐标;
(4)当导电线缆(即抛物线L)接触开关时,即可通电,直接写出通电时整数p的值.
答案
一、 单选题 （本题共计16小题，总分38分）
1.（3分）【答案】A
2.（3分）【答案】C
3.（3分）【答案】B
4.（3分）【答案】B
5.（3分）【答案】D
6.（3分）【答案】B
7.（2分）【答案】A
8.（2分）【答案】D
9.（2分）【答案】C
10.（2分）【答案】A
11.（2分）【答案】D
12.（2分）【答案】C
13.（2分）【答案】C
14.（2分）【答案】B
15.（2分）【答案】D
16.（2分）【答案】C
二、 填空题 （本题共计3小题，总分10分）
17.（2分）【答案】7
18.（4分）(1)是；
【解析】是
(2)19.7.
【解析】2(18+32)=2(32+42)=142≈19.7
∴需要彩条的长度约为19.7dm.
19.（4分）(1)23
(2)13+1
三、 解答题 （本题共计7小题，总分72分）
20.（9分）(1)C=A⋅B=(k−1)(2k+3)=2k2+k−3，
∴2k2+k−3−2k2=k−3,
即程序自动呈现的整式C缺失的部分“”为k−3
(2)∵B2−2C=(2k+3)2−2(2k2+k−3)=4k2+12k+9−(4k2+2k−6)=10k+15,
令10k+15>5,解得k>−1,∵k为正整数,∴最小值为1
21.（9分）(1)15
(2)图略
共有20种等可能结果，满足条件的共4种，P(小玲胜小军)=15
22.（9分）(1)①400;
②接入水杯的温水吸收的热量为:14×20×(t−30)=280t−8400;
由题意:280t−8400=8×15×(100−t)，解得t=51∘
答：王老师的水杯容量为400ml,水温约51∘.
(2)设嘉琪接温水的时间为xs,接开水的时间为ys,
则{20x+15y=21020x(40−30)=15y(100−40),解得{x=9y=2,x+y=11
∴嘉琪同学的接水时间为11s.
23.（10分）(1)证明:如图1,由旋转得:∠EDF=90∘,ED=DF,
∵四边形ABCD是正方形,
∴∠ADC=90∘,AD=CD,
∴∠ADC=∠EDF,
即∠ADE+∠EDC=∠EDC+∠CDF,
∴∠ADE=∠CDF,
在ΔADE和ΔCDF中,
{AD=CD∠ADE=∠CDF,DE=DF
∴ΔADE≅ΔCDF(SAS),
∴AE=CF;
(2)解:ΔADE≅ΔCDF,
∴SΔADE=SΔCDF,
∵当OE⊥AD时,点E到AD的距离最小,则SΔADE的值最小,即SΔADE的值最小,
(3)解:如图2,过F作OC的垂线,交BC的延长线于P,
∵O是BC的中点,且AB=BC=25,
∵A,E,O三点共线,∴OB=5,
由勾股定理得:AO=AB2−BO2=5,
∵OE=2,∴AE=5−2=3,
由(1)知:ΔADE≅ΔCDF,
∴∠DAE=∠DCF,CF=AE=3,
∵∠BAD=∠DCP,
∴∠OAB=∠PCF,
∵∠ABO=∠P=90∘,
∴ΔABO∼ΔCPF,
∴ABOB=CPPF=255=2,
∴CP=2PF,
设PF=x,则CP=2x,
由勾股定理得:32=x2+(2x)2,
解得x=355或−355(舍),
∴点F到直线BC的距离为355.
24.（10分）(1)将点M(m,12)代入y=−43x+16,
得12=−43m+16,解得m=3.∴点M(3,12),
将点M(3,12),点(−6,0)代入y=kx+b,
得{0=−6k+b12=3k+b,解得{b=8k=43,
∴直线l2的函数表达式为y=43x+8;
(2)由题意可得P(12,0),Q(−6,0),
∵直线x=a分别交x轴、直线l1,l2于点A,点B,点C,
∴当x=n时,点A(n,0),由y=−43x+16=−43n+16,则点B(n,−43n+16),
由y=43x+8=43n+8,则点C(n,43n+8),
当AB=2BC时,
情况一：当点A,B,C在点M左侧时,点C为AB的中点.
∴2(43n+8)=−43n+16,解得n=0,且−6≤n≤12,符合题意;
情况二：如图2,当点A,B,C在点M右侧时,
∵AB=2BC,∴−43n+16=2[43n+8−(−43n+16)],解得n=245,且−6≤n≤12,符合题意.
综上所述,当n=0或245时,AB=2BC；
(3)74≤n≤254
设点D(5,6)关于直线x=a的对称点K(t,6),
当点K(t,6)落在直线l2上时,t=−32,此时n=74,
当点K(t,6)落在l1上时,t=152,此时n=254,
∴点K在直线l1,直线l2与x轴所围成的三角形内部(包括边界)时,n的取值范围为74≤n≤254.
25.（12分）(1)200∘;
解析:由扇形的面积公式得:2π9=∠MBF360×π×22,
则∠MBF=20∘,a=180∘+20∘=200∘;
(2)相离.如图1,
∵BE⊥BC,∴∠EBC=90∘,
∵BE=4,BC=3,∴EC=5,
过点B作BG⊥CE于点G,∴12CB×BE=12CE×BG,∴BG=125>2,
∴CE与扇形ABF所在圆⨀B相离;
(3)①当折叠后DE所在的直线与扇形ABF所在的圆B相切时,切点为Q,
又由题意得:∠QEP=∠PED=60∘,∴∠PEB=30∘,
如图2,当点Q在BE的左侧时,连接BQ,则∠BQE=90∘,
∵BQ=2,BE=4,sin⁡∠QEB=BQBE=12,∴∠QEB=30∘,
∵四边形EBCD为矩形,∴∠DEB=90∘,∴∠QED=120∘,
又由题意得:∠QEP=∠PED=60∘,∴∠EPB=30∘,
∵BE=4,∴PB=433,∴CP=3−433;
②如图3,当点Q在BE右侧时,同理可得:∠QEB=30∘,
又由题意得:∠QEP=∠PED=30∘,
∵BE=4,∴PB=43,∠BEP=60∘,∴CP=43−3.
③当D′E于圆相切时,如图3,
由折叠知:∠1=∠2,
在RtΔBQE中,∵BQ=12BE,∴∠BEC=30∘,
又∠B′EC=90∘,∴∠1=∠2=30∘,
在RtΔPBE中,PB=tan⁡∠PEB⋅BE=33×4=433,PC=3+433;
④当D′E同左侧圆相切时,如图4,
同理可得:PB=43,PC=43+3;
综上,PC=3−433或43−3或3+433或43+3.
26.（13分）(1)(0,6)
(2)当p=−4时,y=x2+8x+5=(x+4)2−11,
∴抛物线的对称轴为x=−4,
∵a=1>0,y最小=−11;
(3)①∵y=x2−2px+p2+2p−3=(x−p)2+2p−3,
∴抛物线L顶点E(p,2p−3),
②令x=p,y=2p−3,则:点E所在直线的解析式为y=2x−3;
当y=0时,2x−3=0,解得x=32,此时E(32,0)
当y=6时,2x−3=6,解得x=92,此时E(92,6)
(4)-3或1
解析:∵抛物线L顶点始终在直线y=2x−3上,∴当x=8时,y=13,13>6,
∴在L位置变化的过程中,会经过顶点A,D,不会经过顶点B,C,
当L经过点D时,把x=0,y=0代入解析式,得0=a2+2a−3,解得a=−3或a=1;
当L经过点A时,把x=0,y=6代入解析式,得6=a2+2a−3,解得a=−1±10(舍去);
综上,整数a=−3或a=1.