




2024年山东省泰安市第六中学新校区中考二模数学试题(原卷版+解析版)
展开1. 下列四个数:,,,,其中最小的数是( )
A. B. C. D.
2. 下列运算正确的是( )
A. B.
C. D.
3. 2022年我国粮食总产量再创新高,达686530000吨.将数字686530000用科学记数法表示为( )
A B.
C. D.
4. 生活中有许多对称美的图形,下列是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
5. 一块含有30°的直角三角板和直尺如图放置,若,则∠2的度数是( )
A. 35°B. 45°C. 55°D. 65°
6. 下表是抽查的某班10名同学中考体育测试成绩线计表.
若成绩的平均数为23,中位数是,众数是,则的值是( )
A. ﹣5B. ﹣2.5C. 2.5D. 5
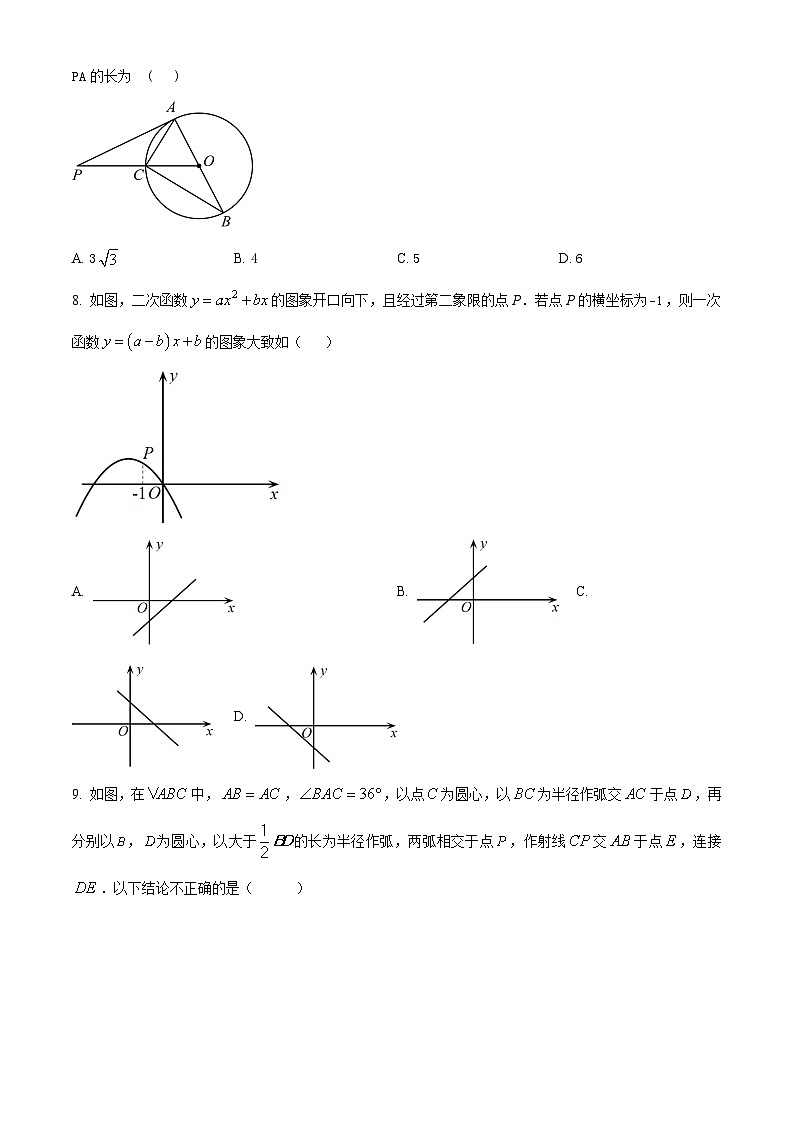
7. 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC. 若∠BAC=2∠BCO,AC=3,则PA的长为 ( )
A. 3B. 4C. 5D. 6
8. 如图,二次函数的图象开口向下,且经过第二象限的点P.若点P的横坐标为,则一次函数的图象大致如( )
A. B. C. D.
9. 如图,在中,,,以点为圆心,以为半径作弧交于点,再分别以,为圆心,以大于的长为半径作弧,两弧相交于点,作射线交于点,连接.以下结论不正确的是( )
A. B.
C. D.
10. 已知二次函数的部分图象如图所示,图象经过点,其对称轴为直线.下列结论:①;②若点,均在二次函数图象上,则;③关于x的一元二次方程有两个相等的实数根;④满足的x的取值范围为.其中正确结论的个数为( ).
A. 1个B. 2个C. 3个D. 4个
11. 如图,正方形的边长为4,点,分别在边,上,且,平分,连接,分别交,于点,,是线段上的一个动点,过点作垂足为,连接,有下列四个结论:①垂直平分;②的最小值为;③;④.其中正确的是( )
A. ①②B. ②③④C. ①③④D. ①③
12. 如图,在平面直角坐标系中,点A、点B在x轴上,OB=5,OA=2,点C是y轴上一动点,连接,将绕点A顺时针方向旋转得到,连接,则的最小值为( )
A B. C. D.
二、填空题(本大题共6小题,满分24分,只要求填写最后结果,每小题填对得4分)
13. 若关于x的一元二次方程有两个不相等的实数根,则m的取值范围是 ____________________.
14. 图1是一种淋浴喷头,图2是图1的示意图,若用支架把喷头固定在点处,手柄长与墙壁的夹角 ,喷出的水流与形成的夹角,现在住户要求:当人站在处淋浴时,水流正好喷洒在人体的处,且使.问:安装师傅应将支架固定在离地面多高的位置?
(结果精确到,参考数据:)
15. 若不等式组的解集为,则m的取值范围是______.
16. 如图,将平行四边形进行折叠,折叠后恰好经过点C得到,若,则线段的长度为 _______.
17. 如图,已知扇形的半径,,将扇形绕点A顺时针旋转得到扇形,则图中阴影部分的面积是______.
18. 在平面直角坐标系中,为等边三角形,点A的坐标为.把按如图所示的方式放置,并将进行变换:第一次变换将绕着原点O顺时针旋转,同时边长扩大为边长的2倍,得到;第二次旋转将绕着原点O顺时针旋转,同时边长扩大为边长的2倍,得到,….依次类推,得到,则点的坐标为 ___________________.
三、解答题(本大题共7小题,共78分,解答应写出必要的文字、证明过程或推演步骤)
19. (1)化简:;
(2)解不等式组.
20. 随着新课程标准的颁布,为落实立德树人根本任务,东营市各学校组织了丰富多彩的研学活动,得到家长、社会的一致好评.某中学为进一步提高研学质量,着力培养学生的核心素养,选取了A.“青少年科技馆”,B.“黄河入海口湿地公园”,C.“孙子文化园”,D.“白鹭湖营地”四个研学基地进行研学.为了解学生对以上研学基地的喜欢情况,随机抽取部分学生进行调查统计(每名学生只能选择一个研学基地),并将调查结果绘制成了两幅不完整的统计图(如图所示).
请根据统计图中的信息解答下列问题:
(1)在本次调查中,一共抽取了____名学生,在扇形统计图中A所对应圆心角的度数为____;
(2)将上面的条形统计图补充完整;
(3)若该校共有480名学生,请你估计选择研学基地C的学生人数;
(4)学校想从选择研学基地D的学生中选取两名学生了解他们对研学活动的看法,已知选择研学基地D的学生中恰有两名女生,请用列表法或画树状图的方法求出所选2人都是男生的概率.
21. 如图,矩形边在平面直角坐标系中的轴上,矩形对角线交于点,过点M的反比例函数与矩形的边交于点,,直线交x轴于点F.
(1)求反比例函数的表达式和点B的坐标;
(2)若点P为x轴上一点,当最小时,求出点P的坐标;
(3)若点Q为平面内任意一点,若以点B,E,F,Q为顶点的四边形是平行四边形,请直接写出点Q的坐标.
22. 在某市组织的农机推广活动中,甲、乙两人分别操控A、B两种型号的收割机参加水稻收割比赛.已知乙每小时收割的亩数比甲少40%,两人各收割6亩水稻,乙则比甲多用0.4小时完成任务;甲、乙在收割过程中对应收稻谷有一定的遗落或破损,损失率分别为3%,2%.
(1)甲、乙两人操控A、B型号收割机每小时各能收割多少亩水稻?
(2)某水稻种植大户有与比赛中规格相同的100亩待收水稻,邀请甲、乙两人操控原收割机一同前去完成收割任务,要求平均损失率不超过2.4%,则最多安排甲收割多少小时?
23. 如图,在正方形ABCD中,,M是对角线BD上的一个动点().连接AM,过点M作交BC于点N.
(1)如图1,求证:;
(2)如图2,过点N作于H,当时,求面积.
24. 如图,已知抛物线交x轴于,两点,交y轴于点C,点P是抛物线上一点,连接AC、BC.
(1)求抛物线的表达式;
(2)连接OP,BP,若,求点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使得∠QBA=75°?若存在,直接写出点Q的坐标;若不存在,请说明理由.
25. 如图,点E是正方形ABCD边BC延长线上一点,连接DE,过顶点B作BF⊥DE,垂足为F,BF交边DC于点G.
(1)求证:DG•BC=DF•BG;
(2)连接CF,求∠CFB的大小;
(3)作点C关于直线DE的对称点H,连接CH,FH.猜想线段DF,BF,CH之间的数量关系并加以证明.
成绩(分)
30
25
20
15
人数(人)
2
1
2024年山东省泰安市东平县中考二模数学试题(原卷版+解析版): 这是一份2024年山东省泰安市东平县中考二模数学试题(原卷版+解析版),文件包含2024年山东省泰安市东平县中考二模数学试题原卷版docx、2024年山东省泰安市东平县中考二模数学试题解析版docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
2024年山东省泰安市岱岳区中考二模数学试题(原卷版+解析版): 这是一份2024年山东省泰安市岱岳区中考二模数学试题(原卷版+解析版),共38页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2024年山东省泰安市第六中学新校区中考二模数学试题: 这是一份2024年山东省泰安市第六中学新校区中考二模数学试题,共8页。












