初中数学浙教版九年级上册3.5 圆周角优秀同步训练题

这是一份初中数学浙教版九年级上册3.5 圆周角优秀同步训练题，共27页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

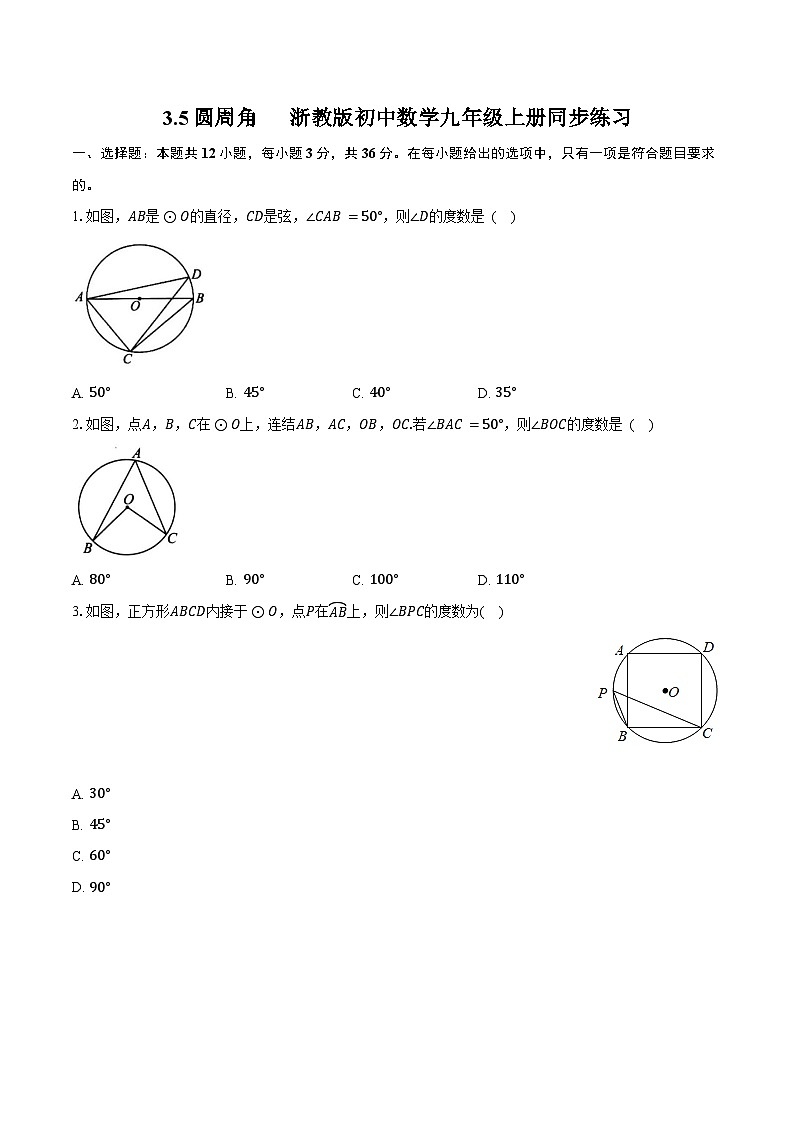
1.如图，AB是⊙O的直径，CD是弦，∠CAB=50°，则∠D的度数是 ( )
A. 50°B. 45°C. 40°D. 35°
2.如图，点A，B，C在⊙O上，连结AB，AC，OB，OC.若∠BAC=50°，则∠BOC的度数是 ( )
A. 80°B. 90°C. 100°D. 110°
3.如图，正方形ABCD内接于⊙O，点P在AB上，则∠BPC的度数为( )
A. 30°
B. 45°
C. 60°
D. 90°
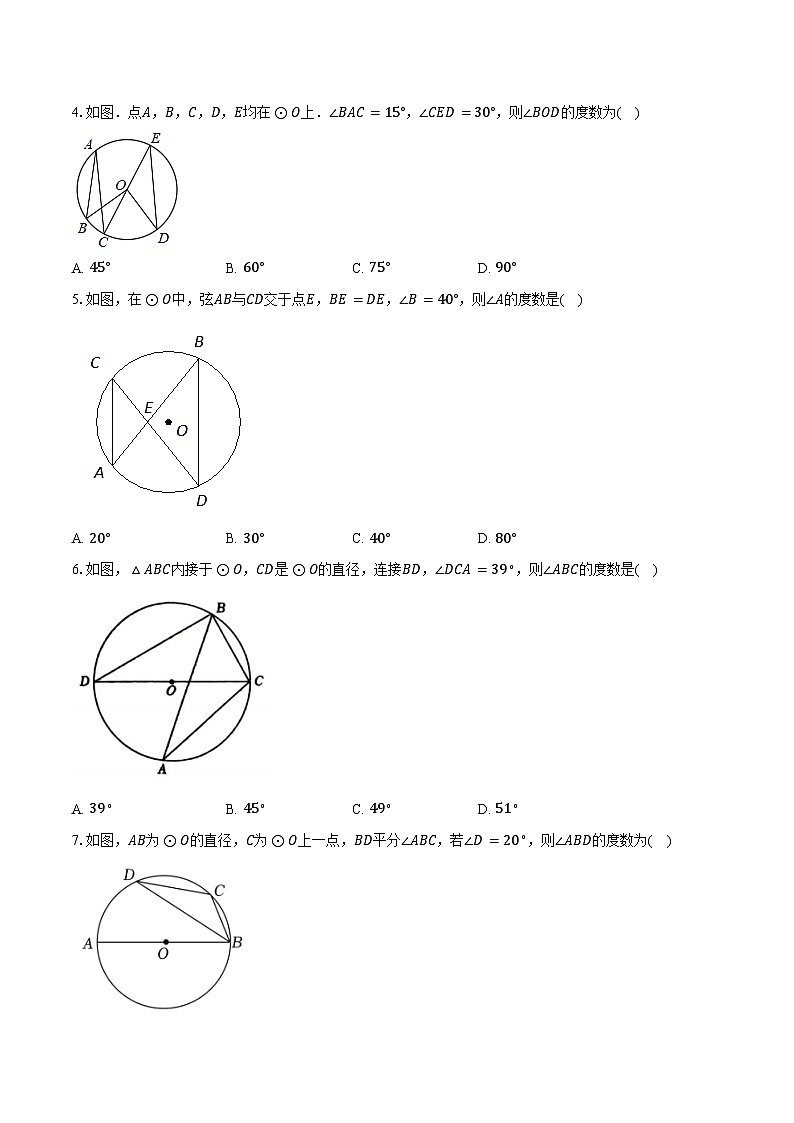
4.如图．点A，B，C，D，E均在⊙O上．∠BAC=15°，∠CED=30°，则∠BOD的度数为( )
A. 45°B. 60°C. 75°D. 90°
5.如图，在⊙O中，弦AB与CD交于点E，BE=DE，∠B=40°，则∠A的度数是( )
A. 20°B. 30°C. 40°D. 80°
6.如图，△ABC内接于⊙O，CD是⊙O的直径，连接BD，∠DCA=39∘，则∠ABC的度数是( )
A. 39∘B. 45∘C. 49∘D. 51∘
7.如图，AB为⊙O的直径，C为⊙O上一点，BD平分∠ABC，若∠D=20∘，则∠ABD的度数为( )
A. 20∘B. 25∘C. 30∘D. 35∘
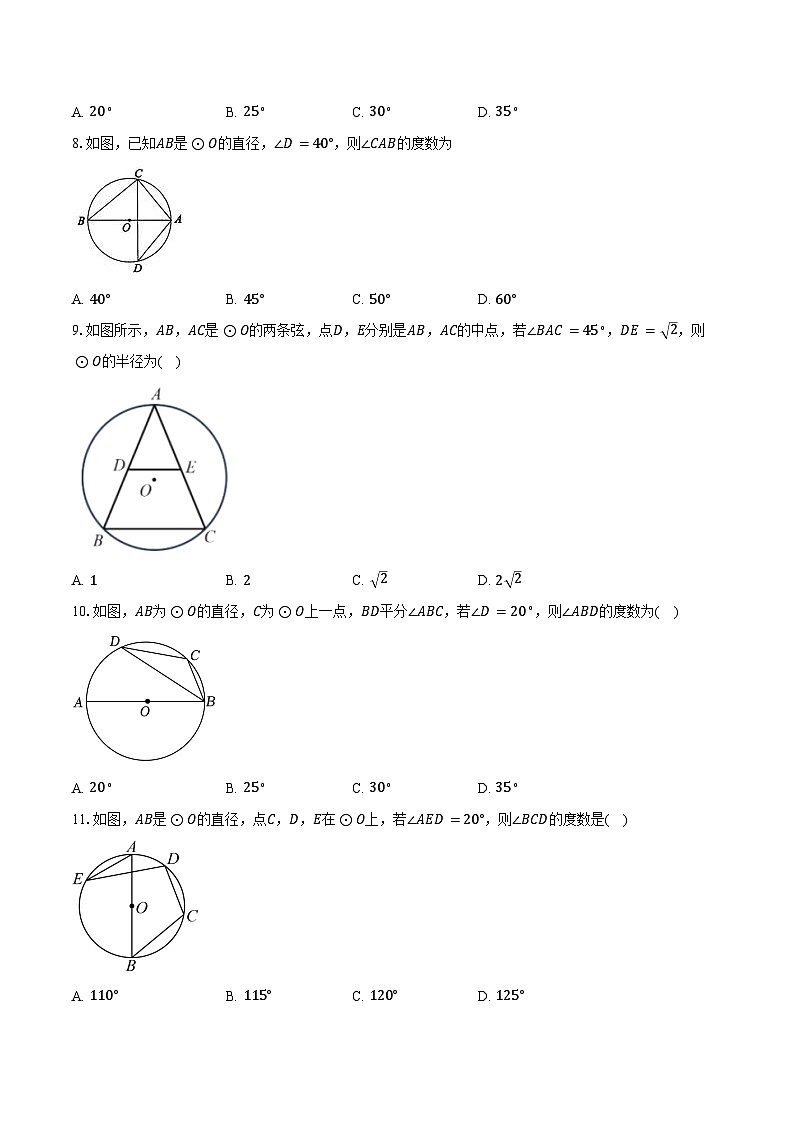
8.如图，已知AB是⊙O的直径，∠D=40°，则∠CAB的度数为
A. 40°B. 45°C. 50°D. 60°
9.如图所示，AB，AC是⊙O的两条弦，点D，E分别是AB，AC的中点，若∠BAC=45∘，DE= 2，则⊙O的半径为( )
A. 1B. 2C. 2D. 2 2
10.如图，AB为⊙O的直径，C为⊙O上一点，BD平分∠ABC，若∠D=20∘，则∠ABD的度数为( )
A. 20∘B. 25∘C. 30∘D. 35∘
11.如图，AB是⊙O的直径，点C，D，E在⊙O上，若∠AED=20°，则∠BCD的度数是( )
A. 110°B. 115°C. 120°D. 125°
12.如图，点A，B，C，D是⊙O上的点，AD是⊙O的直径，若∠BCD=110∘，则∠ADB的度数为( )
A. 10∘B. 20∘C. 50∘D. 70∘
二、填空题：本题共4小题，每小题3分，共12分。
13.如图，⊙O是△ABC的外接圆，OD⊥AB，垂足为E，交⊙O于点D，连接OA.若∠ACB=60∘，AB=4 3，则OE的长度为 ．
14.如图，⊙O是△ABC的外接圆，AB=AC，CD⊥AB于点D，BO的延长线交CD于点E．
(1)∠DCB ______∠DBE(填“>，<或=”)；
(2)若BC=4 2，BE=4，则OE= ______．
15.如图，点A、B、C在圆O上，CO的延长线交AB于点D，∠B=40°，∠ADC=110°，则∠A的度数为_____．
16.如图，在⊙O中，点A是优弧BC上一点，∠BAC=α，连接BO，CO，延长BO交AC于点D，则图中角度大小为2α的角是___________．
三、解答题：本题共9小题，共72分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题8分)
如图，AB为⊙O的直径，AB=AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC=45∘．
(1)求∠EBC的度数．
(2)求证：BD=CD．
18.(本小题8分)
如图，AB是⊙O的直径，D为AB上一点，C为⊙O上一点，且AD=AC，延长CD交⊙O于点E，连接CB．
(1)求证：∠CAB=2∠BCD；
(2)若∠BCE=15°，AB=6，求CE的长．
19.(本小题8分)
如图，已知线段a，b.用直尺和圆规作△ABC，使BC=a，AB+AC=b，且分别满足下列条件．(要求：保留作图痕迹，写出必要的文字说明)
(1)AB=AC； (2)∠A=90°．
20.(本小题8分)
如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交BC，AC边于点D、F.过点D作DE⊥CF于点E．
(1)求证：DE2=AE·FE；
(2)若⊙O半径为5，且AF−DE=2，求EF的长．
21.(本小题8分)
如图，四边形ABCD中，AC=AD，∠ABD=90°，过A，B，D三点的圆与CD交于点E．
(1)求证：E是CD的中点；
(2)若CD=2BC，求证：∠BCD=2∠ADB．
22.(本小题8分)
如图四边形ABCD、PBCQ、APQD均是平行四边形，点P在▱ABCD内，
(1)求证：△APB≌△DQC；
(2)若∠ABP=∠ADP，求证：∠PAB=∠PCB．
23.(本小题8分)
如图所示，小明制作一个模具，AD=4cm，CD=3cm，∠ADC=90∘，AB=13cm，BC=12cm，求这个模具的面积．
24.(本小题8分)
小军借助反比例函数图象设计“鱼形”图案，如图，在平面直角坐标系中，以反比例函数y=kx图象上的点A( 3,1)和点B为顶点，分别作菱形AOCD和菱形OBFE，点D，E在x轴上，以点O为圆心，OA长为半径作AC，连接BF．
(1)求k的值；
(2)求扇形AOC的半径及圆心角的度数；
(3)请直接写出图中阴影部分面积之和．
25.(本小题8分)
如图，AB是⊙O的直径，点C,D在⊙O上，且∠COD=90∘，连接AD并延长到点F，连接BF，若∠F=12∠AOD．
(1)求证：BF是⊙O的切线；
(2)若BF=43 3,∠BCD=30∘，求BC的长．
答案和解析
1.【答案】C
【解析】解：∵AB是直径，
∴∠ACB=90°，
∵∠CAB=50°，
∴∠ABC=90°−50°=40°，
∴∠D=∠ABC=40°，
故选：C．
求出∠ABC，利用圆周角定理，可得结论．
本题考查圆周角定理，解题的关键是圆周角定理，属于中考常考题型．
2.【答案】C
【解析】解：∵∠BAC=50°，∠BOC=2∠BAC，
∴∠BOC=100°．
故选：C．
直接利用圆周角定理求解即可求得∠BOC的度数．
此题考查了圆周角定理．注意在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
3.【答案】B
【解析】【分析】
本题考查了圆周角定理和正方形的性质，确定弧BC所对的圆心角为90°，是本题解题的关键．
根据正方形的性质得到弧BC所对的圆心角为90°，则∠BOC=90°，然后根据圆周角定理求解．
【解答】
解：连接OB、OC，如图，
∵正方形ABCD内接于⊙O，
∴弧BC所对的圆心角为90°，
∴∠BOC=90°，
∴∠BPC=12∠BOC=45°．
故选：B．
4.【答案】D
【解析】【分析】
此题考查了圆周角定理．注意准确作出辅助线是解此题的关键．
首先连接BE，由圆周角定理即可得∠BEC的度数，继而求得∠BED的度数，然后由圆周角定理，求得∠BOD的度数．
【解答】
解：连接BE，
∵∠BEC=∠BAC=15°，∠CED=30°，
∴∠BED=∠BEC+∠CED=45°，
∴∠BOD=2∠BED=90°．
故选：D．
5.【答案】C
【解析】【分析】
本题主要考查了等腰三角形的性质，圆周角定理，熟记圆周角定理是解题的关键．根据等腰三角形的性质和圆周角定理即可得到结论．
【解答】
解：∵BE=DE，∠B=40°，
∴∠D=∠B=40°，
∴∠A=∠D=40°，
故选：C．
6.【答案】D
【解析】解：∵CD是⊙O的直径，
∴∠DBC=90°，
∵∠DBA=∠DCA=39°，
∴∠ABC=90°−∠DBA=51°，
故选：D．
由直径所对的圆周角是直角可得∠DBC=90°，由同弧所对的圆周角相等可得∠DBA=∠DCA=39°，进而可计算∠ABC．
本题主要考查了直径所对的圆周角是直角、同弧所对的圆周角相等，解决本题的关键是熟练掌握相关知识点，难度不大．
7.【答案】D
【解析】【分析】
此题考查了圆周角定理，连接AC，根据圆周角定理得出∠ACB=90∘，∠A=20∘，根据直角三角形的性质求出∠ABC=70∘，根据角平分线的定义求解即可．
【解答】
解：如图，连接AC，
∵AB为⊙O的直径，
∴∠ACB=90∘，
∴∠A+∠ABC=90∘，
∵∠D=∠A=20∘，
∴∠ABC=70∘，
∵BD平分∠ABC，
∴∠ABD=12∠ABC=35∘，
故选D．
8.【答案】C
【解析】【分析】
本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．先根据圆周角定理求出∠B及∠ACB的度数，再由直角三角形的性质即可得出结论．
【解答】
解：∵∠D=40°，
∴∠B=∠D=40°．
∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠CAB=90°−40°=50°．
故选C．
9.【答案】B
【解析】【分析】
本题主要考查了三角形的中位线定理，以及勾股定理，圆周角定理，关键是掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
先根据圆周角定理得到∠BOC=2∠BAC=90°，则可判断△OBC为等腰直角三角形，然后根据勾股定理可得BC= 2OB，再根据三角形的中位线定理可得BC=2DE=2 2，即可求出半径OB．
【解答】
解：如下图，连接OB和OC，
∵∠BAC=45°，
∴∠BOC=2∠BAC=90°，
∵点D、E分别是AB、AC的中点，
∴DE=12BC= 2，
∴BC=2 2．
∵OB和OC是⊙O的半径，
∴OB=OC，
∴BC= 2OB=2 2，
∴OB=OC=2．
故选：B．
10.【答案】D
【解析】根据圆周角定理得出∠ACB=90∘，∠A=20∘，根据直角三角形的性质求出∠ABC=70∘，根据角平分线的定义求解即可．
【解答】解：如图，连接AC，
∵AB为⊙O的直径，
∴∠ACB=90∘，
∴∠A+∠ABC=90∘，
∵∠D=∠A=20∘，
∴∠ABC=70∘，
∵BD平分∠ABC，
∴∠ABD=12∠ABC=35∘，
故选：D．
11.【答案】A
【解析】【分析】
此题主要考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．连接AC，根据圆周角定理，可分别求出∠ACB=90°，∠ACD=20°，即可求∠BCD的度数．【解答】
解：连接AC，
∵AB为⊙O的直径，
∴∠ACB=90°，
∵∠AED=20°，
∴∠ACD=∠AED=20°，
∴∠BCD=∠ACB+∠ACD=110°，
故选：A．
12.【答案】B
【解析】解：∵AD是⊙O的直径，
∴∠ACD=90°，
∵∠BCD=110°，
∴∠ACB=∠BCD−∠ACD=20°，
∴∠ADB=∠ACB=20°．
故选：B．
根据AD是⊙O的直径，可得∠ACD=90°，进而可得∠ACB=∠BCD−∠ACD=20°，问题随之得解．
本题主要考查了圆周角定理，掌握直径所对圆周角为直角，同圆中，等弧所对的圆周角相等，是解答本题的关键．
13.【答案】2
【解析】【分析】
本题主要考查的是含30度角的直角三角形的性质，勾股定理，圆周角定理，垂径定理，三角形的外接圆和外心的有关知识，连接OB，利用圆周角定理及垂径定理易得∠OAE=30°，结合已知条件，利用直角三角形中30°角对的直角边等于斜边的一半即得到AO=2OE，利用勾股定理求解即可．
【解答】
解：如图，连接OB，
∵∠ACB=60°，
∴∠AOB=2∠ACB=120°，
∵AO=OB，
∴∠OAB=∠OBA=(180°−120°)÷2=30°，
∵OD⊥AB，
∴AE=12AB=12×4 3=2 3，
∵∠OAB=30°，
∴AO=2OE，
∵AO2−OE2=AE2，
∴(2OE)2−OE2=(2 3)2，
解得OE=2
14.【答案】= 1
【解析】解：(1)延长BE交⊙O于点F，连接CF，
∵BF是⊙O的直径，
∴∠BCF=90°，
∴∠F+∠FBC=90°，
∵CD⊥AB，
∴∠BDC=∠ADC=90°，
∴∠A+∠ACD=90°，
∵∠A=∠F，
∴∠ACD=∠FBC，
∵AB=AC，
∴∠ABC=∠ACB，
∴∠ABC−∠FBC=∠ACB−∠ACD，
∴∠DBE=∠DCB，
故答案为：=；
(2)解：∵∠BDC=90°，
∴∠DBE+∠DEB=90°，
∵∠FCB=90°，
∴∠FCE+∠DCB=90°，
∵∠DBE=∠DCB，
∴∠DEB=∠FCE，
∵∠DEB=∠FEC，
∴∠FEC=∠FCE，
∴FE=FC，
设FE=FC=x，
在Rt△CBF中，BC=4 2，BF=BE+EF=4+x，
∴BC2+CF2=BF2，
∴32+x2=(4+x)2，
解得：x=2，
∴BF=4+x=6，
∴OB=12BF=3，
∴OE=BE−OB=4−3=1，
∴OE的长为1，
故答案为：1．
(1)延长BE交⊙O于点F，连接CF，根据直径所对的圆周角是直角可得∠BCF=90°，从而可得∠F+∠FBC=90°，再根据垂直定义可得∠BDC=∠ADC=90°，从而可得∠A+∠ACD=90°，然后利用同弧所对的圆周角相等可得∠A=∠F，从而可得∠ACD=∠FBC，再利用等腰三角形的性质可得AB=AC，从而可得∠ABC=∠ACB，最后利用等式的性质可得∠DBE=∠DCB，即可解答；
(2)根据直角三角形的两个锐角互余可得∠DBE+∠DEB=90°，∠FCE+∠DCB=90°，从而利用等角的余角相等可得∠DEB=∠FCE，再利用对顶角相等可得∠DEB=∠FEC，从而可得∠FEC=∠FCE，进而可得FE=FC，然后设FE=FC=x，在Rt△CBF中，利用勾股定理列出关于x的方程，进行计算即可解答．
本题考查了三角形的外接圆与外心，圆周角定理，勾股定理，等腰三角形的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
15.【答案】55°
【解析】【分析】
本题考查了圆心角和圆周角的关系及三角形外角的性质，圆心角和圆周角的关系是解题的关键．
根据三角形的外角的性质求得∠BOD=70°，然后根据邻补角求得∠BOC的度数，再根据圆周角定理求得∠A即可.
【解答】
解：∵∠B=40°，∠ADC=110°，
∴∠BOD=∠ADC−∠B=110°−40°=70°，
∴∠BOC=180°−∠BOD=110°，
∴∠A=12∠BOC=55°，
故答案为55°．
16.【答案】∠BOC
【解析】【分析】
本题考查圆周角定理，关键是掌握圆周角定理：一条弧所对的圆周角等于这条弧所对圆心角的一半，由圆周角定理，即可得到答案．
【解答】
解：由圆周角定理得：∠BOC=2∠BAC=2α．
故答案为：∠BOC．
17.【答案】【小题1】
22．5∘．
【小题2】
略

【解析】1. 略
2. 略
18.【答案】(1)证明：∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠ACD=90°−∠BCD，
∵AC=AD，
∴∠ACD=∠ADC，
∴∠A+∠ACD+∠ADC=180°，
∴∠A+90°−∠BCD+90°−∠BCD=180°，
∴∠A=2∠BCD；
(2)解：连接OC、OE，如图，

由(1)得∠A=2∠BCE=2×15°=30°，
∵∠BOE=2∠BCE=2×15°=30°，
∵OA=OC，
∴∠A=∠ACO，
∴∠COB=∠A+∠ACO=2∠A=60°，
∵∠COE=∠COB+∠BOE=60°+30°=90°，
而OC=OE=12AB=12×6=3，
∴CE= OC2+OE2= 32+32=3 2．
【解析】本题考查了圆周角定理及其推论，等腰三角形的性质，三角形内角和定理，勾股定理，三角形外角的性质．熟练掌握圆周角定理及其推论是解题的关键．
(1)根据圆周角定理得到∠ACB=90°，则∠ACD=90°−∠BCD，再利用等腰三角形的性质和三角形内角和得到∠A+90°−∠BCD+90°−∠BCD=180°，从而得到结论；
(2)连接OC、OE，如图，利用(1)的结论和圆周角定理得到∠A=∠BOE=30°，则∠COB=60°，所以∠COE=90°，然后利用勾股定理计算CE的长．
19.【答案】解：(1)如图 ①，作线段b，再作线段b的垂直平分线;作线段BC=a，分别以B，C为圆心，b2为半径画圆弧，交于点A，连接AB，AC，△ABC即为所求．
(2)如图 ②，作线段BC=a，作BC的垂直平分线和以M为圆心，MB为半径画圆，以B为圆心，b为半圆O于点A，连接AB，AC，△ABC即为所求．

【解析】本题考查了作图−复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了等腰直角三角形的性质，圆周角定理等．
(1)作线段b，再作线段b的垂直平分线;作线段BC=a，分别以B，C为圆心，b2为半径画圆弧，交于点A，连接AB，AC，△ABC即为所求．
(2)作线段BC=a，作BC的垂直平分线和以M为圆心，MB为半径画圆，以B为圆心，b为半圆O于点A，连接AB，AC，△ABC即为所求．
20.【答案】(1)证明：连接BF，AD，OD，如图，
∵AB是⊙O的直径，
∴∠ADB=90°，∠AFB=90°，
∵AB=AC，
∴D为BC的中点，
∵DE⊥AC，BF⊥AC，
∴DE/​/BF，
∴点E是CF的中点，
∴EF=CE，∠ADC=90°，
∴△ADE∽△DCE，
∴DEAE=CEDE，
∴DE2=AE⋅CE，
∴DE2=AE⋅FE；
(2)解：过点O作OG⊥AF于点G，如图，
∴∠OGE=∠OGA=90°，AG=GF=12AF，
又∵∠DEG=∠ODE=90°，
∴四边形OGED为矩形，
∴OG=DE，OD=GE，
∵OD=OA=5，
设EF=x，
AG=GF=5−x，则OG=DE=AF−2=10−2x−2=8−2x．
在Rt△OAG中，AG2+OG2=OA2，
即(5−x)2+(8−2x)2=52，
解得x1=2，x2=0(舍去)，
∴EF=2．
【解析】本题考查了矩形的判定与性质，勾股定理，圆周角定理，等腰三角形的性质等知识点，能综合运用知识点进行推理是解此题的关键．
(1)连接BF，AD，证得△ADE∽△DCE，然后依据相似三角形的性质得到DEAE=CEDE，进而推导出DE2=AE⋅FE；
(2)过点O作OG⊥AF于点G，证明四边形OGED为矩形，由矩形的性质得出OG=DE，OD=GE，设EF=x，AG=GF=5−x，则OG=DE=8−2x.由勾股定理得出(5−x)2+(8−2x)2=52，解方程可得出答案．
21.【答案】证明：(1)如图，连结AE，
∵A，B，D三点共圆，且∠ABD=90∘，
∴AD为直径，
∴∠AED=90∘，
即AE⊥CD，
又AC=AD，
∴CE=DE，
即E是CD的中点．
(2)连结BE，如图
∵CD=2BC，CE=DE，
∴CB=CE，
∴∠CEB=∠CBE，
则∠BCD=180−∠CEB−∠CBE=180−2∠CEB，
又∠AEB=∠AEC−∠CEB=90−∠CEB，
∴∠BCD=2∠AEB，
∵∠AEB与∠ADB对圆中的同一条弧AB
∴∠AEB=∠ADB
∴∠BCD=2∠ADB．
【解析】本题考查的是圆周角定理，等腰三角形的性质有关知识
(1)根据三点共圆可得∠ABD=90∘从而得出AD为直径得出∠AED=90∘即AE⊥CD，再根据AC=AD得出CE=DE即可解答
(2)连结BE，根据CD=2BC，CE=DE得出CB=CE从而得出∠CEB=∠CBE，再根据条件得出∠BCD=2∠AEB，最后解答即可
22.【答案】解：(1)证明：∵四边形ABCD、PBCQ、APQD均是平行四边形，
∴AB=DC，BP=CQ，AP=DQ，
∴在△APB与△DQC中
AB=DCBP=CQAP=DQ
∴△APB≌△DQC(SSS)；
(2)证明：如图，
∵四边形ABCD为平行四边形，
∴∠ABC=∠ADC且∠BAD=∠BCD，
∵∠ABP=∠ADP，
∴∠1=∠2，
∵四边形PBCQ是平行四边形，
∴∠1=∠3，
∴∠2=∠3，
∴点C、P、D、Q四点共圆，则∠CDQ=∠CPQ，
由(1)知△APB≌△DQC，
∴∠PAB=∠CDQ，
∵PQ/​/BC，
∴∠PCB=∠CPQ，
∴∠PAB=∠PCB．
【解析】本题考查了平行四边形的性质，全等三角形的判定与性质，圆周角定理
(1)利用平行四边形的性质得到AB=DC，BP=CQ，AP=DQ，再利用SSS判定△APB≌△DQC即可；
(2)利用平行四边形的性质证明∠1=∠2，∠1=∠3，则∠2=∠3，进而可得点C、P、D、Q四点共圆，则∠CDQ=∠CPQ，再根据平行四边形的性质以及全等三角形的性质即可证明．
23.【答案】24cm2
【解析】【分析】连接 AC ，利用勾股定理求出 AC 的长，在 ΔABC 中，判断它的形状，并求出它的面积，最后求出四边形 ABCD 的面积．
【详解】解：连接 AC ，
在 ΔADC 中， ∵AD=4cm ， CD=3cm ， ∠ADC=90∘ ，
∴AC2=AD2+CD2 ，
∴AC= AD2+CD2= 32+42=5(cm) ，
∴SΔACD=12CD×AD=12×3×4=6(cm2) ，
在 ΔABC 中， ∵AC=5cm ， BC=12cm ， AB=13cm ， 52+122=132 ，
即： AC2+BC2=AB2 ，
根据勾股定理的逆定理可得， ΔABC 是直角三角形，且 ∠ACB=90∘ ，
∴SΔABC=12AC×BC=12×5×12=30(cm2) ，
∴S四边形ABCD=SΔABC−SΔACD=30−6=24cm2 ，
答：这个模具的面积是 24cm2 ．
【点睛】本题考查了勾股定理、勾股定理的逆定理及三角形的面积公式，解题的关键是掌握勾股定理及其逆定理，连接 AC ，说明 ΔABC 是直角三角形．
24.【答案】解：(1)将A( 3,1)代入到y=kx中，
得：1=k 3，
解得：k= 3；
(2)过点A作OD的垂线，交x轴于G，
∵A( 3,1)，
∴AG=1，OG= 3，
OA= ( 3)2+12=2，
∴半径为2；
∵AG=12OA，
∴∠AOG=30°，
由菱形的性质可知，∠AOG=∠COG=30°，
∴∠AOC=60°，
∴圆心角的度数为：60°；
(3)3 3−23π．
【解析】(1)见答案；
(2)见答案；
(3)∵OD=2OG=2 3，
∴S菱形AOCD=AG×OD=2 3，
∴S扇形AOC=16×π×r2=2π3，
在菱形OBEF中，S△FHO=S△BHO，
∵S△FHO=k2= 32，
∴S△FBO=2× 32= 3，
∴S阴影=S△FBO+S菱形AOCD−S扇形AOC= 3+2 3−23π=3 3−23π．
故答案为：3 3−23π．
(1)将A( 3,1)代入y=kx中即可求解；
(2)利用勾股定理求边长，再根据直角三角形中30度角所对的直角边是斜边的一半求解出角度，最后根据菱形的性质求解；
(3)先计算出S菱形AOCD=2 3，再计算出扇形的面积，根据菱形的性质及结合k的几何意义可求出S△FBO= 3，从而问题即可解答．
本题考查反比例函数及k的几何意义，菱形的性质，圆心角与弧的关系等，正确掌握k的几何意义是解题关键．
25.【答案】(1)证明：如图1，连接BD，
图1
∵AB是⊙O的直径，
∴∠ADB=90∘，
∴∠BDF=90∘，∠DBF+∠F=90∘，
∵AD⌢=AD⌢，
∴∠ABD=12∠AOD=∠F，
∴∠DBF+∠ABD=90∘，即OB⊥BE，
又∵OB是半径，
∴BF是⊙O的切线．
(2)解：∵BD⌢=BD⌢，
∴∠BAD=∠BCD=30∘，
∴AB=BFtan30∘=4，BD=AB⋅sin30∘=2，
∵CD⌢=CD⌢，
∴∠CBD=12∠COD=45∘，
如图2，过点D作DG⊥BC于点G，
图2
∴DG=BD⋅sin45∘= 2，BG=BD⋅cs45∘= 2，
∴CG=DGtan30∘= 6，
∴BC=CG+BG= 6+ 2，
∴BC的长度为 6+ 2．

【解析】【分析】(1)如图1，连接BD，则∠ADB=90∘，∠BDF=90∘，∠DBF+∠F=90∘，由AD⌢=AD⌢，可得∠ABD=12∠AOD=∠F，则∠DBF+∠ABD=90∘，即OB⊥BE，进而结论得证；
(2)由BD⌢=BD⌢，可得∠BAD=∠BCD=30∘，则AB=BFtan30∘=4，BD=AB⋅sin30∘=2，由CD⌢=CD⌢，可得∠CBD=12∠COD=45∘，如图2，过点D作DG⊥BC于点G，则DG=BD⋅sin45∘= 2，BG=BD⋅cs45∘= 2，CG=DGtan30∘= 6，根据BC=CG+BG，求解作答即可．
【点睛】本题考查了直径所对的圆周角为直角，三角形内角和定理，切线的判定，圆周角定理，同弧所对的圆周角相等，正弦，正切，余弦等知识．熟练掌握直径所对的圆周角为直角，三角形内角和定理，切线的判定，圆周角定理，同弧所对的圆周角相等，正弦，正切，余弦是解题的关键．