

浙教版4.3 相似三角形精品课后复习题
展开1.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )
A. 五丈B. 四丈五尺C. 一丈D. 五尺
2.如图,有一块直角三角形余料ABC,∠BAC=90°,G,D分别是AB,AC边上的一点,现从中切出一条矩形纸条DEFG,其中E,F在BC上,若BF=4.5cm,CE=2cm,则GF的长为( )
A. 3cmB. 2 2cmC. 2.5cmD. 3.5cm
3.延时课上,老师布置任务如下:让王林站在B点处去观测8m外的位于D点处的一棵大树(CD),所用工具为一个平面镜P和必要的长度测量工具(B、P、D在一直线上).已知王林目高(AB)1.6m,大树高4.8m,将平面镜P放置在离王林( )m处才能观测到大树的顶端.
A. 1B. 2C. 3D. 4
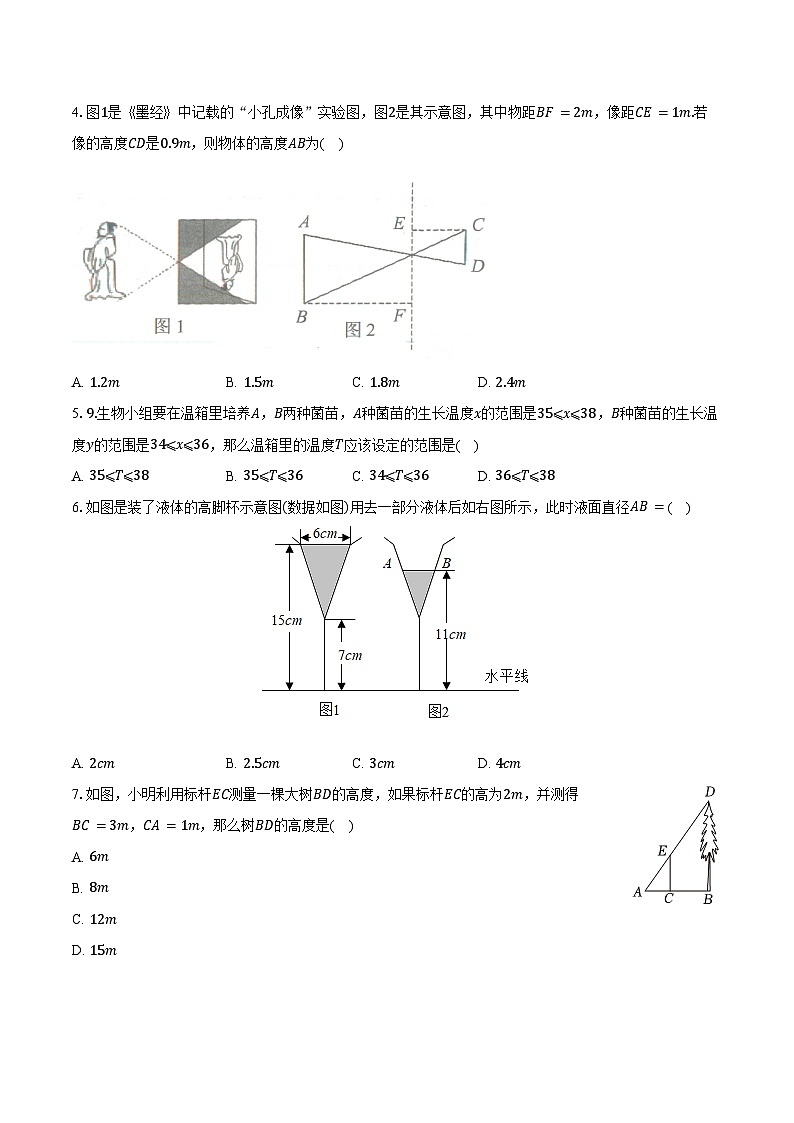
4.图1是《墨经》中记载的“小孔成像”实验图,图2是其示意图,其中物距BF=2m,像距CE=1m.若像的高度CD是0.9m,则物体的高度AB为( )
A. 1.2mB. 1.5mC. 1.8mD. 2.4m
5.9.生物小组要在温箱里培养A,B两种菌苗,A种菌苗的生长温度x的范围是35⩽x⩽38,B种菌苗的生长温度y的范围是34⩽x⩽36,那么温箱里的温度T应该设定的范围是( )
A. 35⩽T⩽38B. 35⩽T⩽36C. 34⩽T⩽36D. 36⩽T⩽38
6.如图是装了液体的高脚杯示意图(数据如图)用去一部分液体后如右图所示,此时液面直径AB=( )
A. 2cmB. 2.5cmC. 3cmD. 4cm
7.如图,小明利用标杆EC测量一棵大树BD的高度,如果标杆EC的高为2m,并测得BC=3m,CA=1m,那么树BD的高度是( )
A. 6m
B. 8m
C. 12m
D. 15m
8.如图,小明在A时测得某树的影长为8m,B时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为( )
A. 2mB. 4mC. 6mD. 8m
9.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=150cm,CD=800cm,则树高AB等于( )
A. 550cmB. 400cmC. 300cmD. 都不对
10.如图,不等臂跷跷板AB的一端A碰到地面时,另一端B到地面的高度为60cm;当AB的一端B碰到地面时,另一端A到地面的高度为90cm,则跷跷板AB的支撑点O到地面的高度OH是( )
A. 36cmB. 40cmC. 42cmD. 45cm
11.如图,放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上,若幻灯片到光源的距离为15cm,到屏幕的距离为150cm,且幻灯片上图形的高度为10cm,则屏幕上图形的高度为( )
A. 100cmB. 105cmC. 110cmD. 115cm
12.由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.过点D作DF的垂线交小正方形对角线EF的延长线于点G,连接CG,延长BE交CG于点H.若AE=2BE,则CGBH的值为( )
A. 32
B. 2
C. 3 107
D. 3 55
二、填空题:本题共4小题,每小题3分,共12分。
13.如图,晚上小亮走在大街上.他发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3米,左边的影子长为1.5米,又知自己身高1.80米,两盏路灯的高相同,两盏路灯之间的距离为12米,则路灯的高为________米.
14.晚上,小亮走在大街上.他发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3米,左边的影子长为1.5米.又知自己身高1.80米,两盏路灯的高相同,两盏路灯之间的距离为12米.则路灯的高为______米.
15.如图1是装了液体的长方体容器的主视图(数据如图),将该容器绕地面一棱进行旋转倾斜后,水面恰好接触到容器口边缘,如图2所示,此时液面宽度AB= ______.
16.综合实践课上,小宇设计用光学原理来测量公园假山的高度,把一面镜子放在与假山AC距离为21米的B处,然后沿着射线CB退后到点E,这时恰好在镜子里看到山头A,利用皮尺测量BE=2.4米,若小宇的身高是1.6米,则假山AC的高度为______米.(结果保留整数)
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
周末,小欣同学来到郊外露营,看到了一棵大树,爱思考的她想利用学过的知识测量如图所示的大树高度.小欣同学找来一根长绳,绑在大树PQ的点A处并将长绳拉直,长绳平行于地面,即满足AB//MN,然后等待合适的时机,等大树在地面的影长恰好与长绳AB的影长顶端在点C处重合(即P、B、C三点在同一直线上),此时做好相应的标记.最后测量得AB=2.75m,CQ=3m,AQ=0.6m,假设图中所有点在同一平面内,且满足PQ⊥MN,请求出大树PQ的高度.
18.(本小题8分)
为了保障市民出行方便,某市在流经该市的河流上架起一座桥,小高和小新想通过自己所学的数学知识计算该桥AF的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在AB、AC的延长线上取点D、E,使得DE//BC.经测量,BC=80米,DE=140米,且点E到河岸BC的距离为75米.已知AF⊥BC于点F,请你根据提供的数据帮助他们计算桥AF的长度.
19.(本小题8分)
如图,AB=AD,∠BAD=2∠BAC.
(1)在AC上方求作求作一点E,连接AE使得△ACE∽△ABD(要求尺规作图,保留作图痕迹,不写作法).
(2)在(1)的条件下,连接DE,若AC= 2AB,BD=DE=1,求证:∠EBC=90°.
20.(本小题8分)
综合实践活动中,小明所在的数学活动小组利用所学知识测量旗杆EF的高度,他在距离旗杆40米的D处立下一根3米高的竖直标杆CD,然后调整自己的位置,当他与标杆的距离BD为4米时,他的眼睛、标杆顶端和旗杆顶位于同一直线上,若小明的眼睛离地面高度AB为1.6米,求旗杆EF的高度.
21.(本小题8分)
如图,丽丽、娜娜利用晚间放学时间完成一个综合实践活动,活动内容是测量公园里路灯的点光源O到地面的高度OA.如图,丽丽站在路灯下D处,娜娜测得丽丽投在地面上的影子BD=1 m;当丽丽在点D处半蹲时,娜娜测得丽丽的影子DF=0.6 m,已知丽丽的身高DE=1.5 m,半蹲时的高度CD=1 m.图中所有点均在同一平面内,OA、DE均与地面AB垂直,点C在DE上,A,D,F,B在同一水平线上,请你根据以上信息帮助她们计算路灯的点光源O到地面的高度OA.
22.(本小题8分)
如图,为了求出海岛上的山峰AB的高度,在D处和F处树立标杆CD和EF,标杆的高都是20米,D,F两处相隔200米,并且AB,CD和EF在同一平面内.从标杆CD后退80米的G处,可以看到顶峰A和标杆顶端C在一条直线上;从标杆EF后退160米的H处,可以看到顶峰A和标杆顶端E在一条直线上.求山峰的高度AB及它和标杆CD的水平距离BD各是多少米?
23.(本小题8分)
晚上小凯在广场上散步,如图,在广场两盏路灯AB,CD的照射下,地面上形成了他的两个影子EH,EG.已知光源B,D的高均为10m,小凯的身高EF为1.5m,两盏路灯相距40m,A,C,E,G,H在同一平面内.
(1)当影子EG长为6m时,求此时小凯到路灯CD的距离EC;
(2)连接GH,判断GH与AC的位置关系,并说明理由;
(3)小凯向上跳起再落下,该过程中GH最长达到9m,直接写出小凯头顶离地面的最大高度.
24.(本小题8分)
如图,已知平行四边形ABCD的三个顶点A、B、C都在半径为5的⊙O上,且AO⊥BC,垂足为点E,BC=6.
(1)求平行四边形ABCD的边AB的长;
(2)延长线段BO交AD于点F,求点F到CD的距离.
25.(本小题8分)
如图,在△ABC中,AC=4.
(1)在AC上求作一点D,连接BD,使得△ABD∽△ACB;(要求:尺规作图,不写作法,保留作图痕迹)
(2)点M,N分别是BD、BC中点,若AD=1,求AMAN的值.
答案和解析
1.【答案】B
【解析】【分析】
本题考查了平行投影.设竹竿的长度为x尺,根据物体的高度与影长成正比即可得到x15=1.50.5,即可得到答案.
【解答】
解:设竹竿的长度为x尺,
∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,
∴x15=1.50.5,解得x=45,即竹竿的长为四丈五尺.
故选B.
2.【答案】A
【解析】解:∵∠BAC=90°,
∴∠AGD+∠ADC=90°,
∵四边形GFDE是矩形,
∴∠GDE=90°,∠GFB=∠DEC=90°,GD//BC,GF=DE,
∴∠ADG+∠EDC=90°,∠AGD=∠B,
∴∠AGD=∠EDC,
∴∠B=∠EDC,
∴△BFG∽△DEC,
∴DE:BF=CE:GF,
∵BF=4.5cm,CE=2cm,
∴GF:4.5=2:GF,
∴GF=3cm,
故选:A.
根据题意推知△BFG∽△DEC,由该相似三角形的对应边成比例,求得GF的长度即可.
本题考查了相似三角形的应用和矩形的性质.利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
3.【答案】B
【解析】解:由题意得:∠APB=∠CPD,AB⊥BD,CD⊥DB,
∴∠ABP=∠CDP=90°,
∴△ABP∽△CDP,
∴ABBP=CDDP,
∴1.6BP=4.88−BP,
解得:BP=2,
∴将平面镜P放置在离王林2m处才能观测到大树的顶端,
故选:B.
根据题意可得:∠APB=∠CPD,AB⊥BD,CD⊥DB,从而可得∠ABP=∠CDP=90°,然后证明△ABP∽△CDP,从而利用相似三角形的性质进行计算即可解答.
本题考查了相似三角形的应用,熟练掌握相似三角形的判定与性质是解题的关键.
4.【答案】C
【解析】【分析】
本题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力.利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
直接利用相似三角形的对应边成比例解答.
【解答】
解:设蜡烛火焰的高度是xcm,
由相似三角形的性质得到:ABCD=BFCE
即:AB0.9=21
解得x=1.8.
即物体的高度AB是1.8cm.
5.【答案】B
【解析】解:温箱里的温度T应该设定在能使A,B两种菌苗同时满足的温度,即35≤x≤38与34≤y≤36的公共部分
由题意可列出不等式组35⩽x⩽3834⩽y⩽36,根据求不等式解集的方法可知温箱里的温度T应该设定在35⩽T⩽36。
因此本题选择B。
6.【答案】C
【解析】解:如图:过O作OM⊥CD,垂足为M,过O′作O′N⊥AB,垂足为N,
∵CD//AB,
∴△CDO∽ABO′,即相似比为CDAB,
∴CDAB=OMO′N,
∵OM=15−7=8cm,O′N=11−7=4cm,
∴6AB=84
∴AB=3cm,
故选:C.
高脚杯前后的两个三角形相似,根据相似三角形的判定和性质即可得出结果.
本题考查相似三角形的应用,解本题的关键熟练掌握相似三角形的判定与性质.
7.【答案】B
【解析】解:由题意可得,CE//BD,
在△ABD中,ACAB=CEBD,
即14=2BD,
解得BD=8m.
故选:B.
由CE//BD,可得ACAB=CEBD,进而可求解线段BD的长度.
此题考查的是平行线段成比例,熟练掌握平行线分线段成比例的性质是解决此题的关键.
8.【答案】B
【解析】【分析】根据题意,画出示意图,易得Rt▵EDC∽Rt▵CDFF,进而可得DECD=CDDF,代入数据求解即可得答案.
【详解】解:根据题意做出示意图,则CD⊥EF,CE⊥CF,DE=2m,DF=8m,
∴∠EDC=∠CDF=∠ECF=90∘,
∴∠E+∠ECD=∠ECD+∠DCF=90∘,
∴∠E=∠DCF,
∴Rt▵EDC∽Rt▵CDF,
∴DECD=CDDF,即2CD=CD8,
∴CD2=2×8=16,
∴CD=4m(负值舍去).
故选:B.
9.【答案】A
【解析】解:AC=150cm=1.5m,CD=800cm=8m
在Rt△DEF与Rt△DBC中,
∵∠EDF=∠CDB,∠FED=∠BCD=90°,
∴△DEF∽△DCB.
∴DEEF=CDBC.
∴4020=8BC.
∴BC=4.
∵AC=1.5m,
∴AB=AC+BC=1.5+4=5.5(m).
即树的高为5.5m=550cm.
故选:A.
先判定△DEF∽△DCB,再根据相似三角形对应边成比例解答.
本题考查了相似三角形的应用,主要利用了相似三角形对应边成比例的性质,比较简单,判定出△DEF和△DBC相似是解题的关键.
10.【答案】A
【解析】【解答】解:如图:过点B作BC⊥AH,垂足为C,
∵OH⊥AC,BC⊥AC,
∴∠AHO=∠ACB=90°,
∵∠BAC=∠OAH,
∴△AOH∽△ABC,
∴OHBC=AOAB,
∴OH60=AOAB,
如图:过点A作AD⊥BH,垂足为D,
∵OH⊥BD,AD⊥BD,
∴∠OHB=∠ADB=90°,
∵∠ABD=∠OBH,
∴△ABD∽△OBH,
∴OHAD=OBAB,
∴OH90=OBAB,
∴OH60+OH90=AOAB+OBAB,
∴OH60+OH90=ABAB,
∴OH60+OH90=1,
解得:OH=36,
∴跷跷板AB的支撑点O到地面的高度OH是36cm,
故选:A.
11.【答案】C
【解析】解:如图所示:∵DE//BC,
∴△AED∽△ACB,
∴AEAC=DEBC,
设屏幕上的图形高是x,则1515+150=10x,
解得:x=110.经检验,x=110是原方程的解,
故选:C.
根据题意可画出图形,再根据相似三角形的性质对应边成比例解答.
本题考查了相似三角形性质的应用.解题的关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
12.【答案】C
【解析】解:如图,过点G作GT⊥CF交CF的延长线于T,设BH交CF于M,AE交DF于N.设BE=AN=CM=DF=a,则AE=BM=CF=DN=2a,
∴EN=EM=MF=FN=a,
∵四边形ENFM是正方形,
∴∠EFM=∠TFG=45°,∠NFE=∠DFG=45°,
∵GT⊥TF,DF⊥DG,
∴∠TGF=∠TFG=∠DFG=∠DGF=45°,
∴TG=FT=DF=DG=a,
∴CT=3a,CG= (3a)2+a2= 10a,
∵MH//TG,
∴△CMH∽△CTG,
∴CM:CT=MH:TG=1:3,
∴MH=13a,
∴BH=2a+13a=73a,
∴CGBH= 10a73a=3 107,
故选:C.
如图,过点G作GT⊥CF交CF的延长线于T,设BH交CF于M,AE交DF于N.设BE=AN=CM=DF=a,则AE=BM=CF=DN=2a,想办法求出BH,CG,可得结论.
本题考查相似三角形的判定和性质,正方形的性质,勾股定理等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.
13.【答案】6.6
【解析】【分析】
本题考查相似三角形的应用.利用相似三角形的相似比,列出方程,通过解方程求出路灯的高即可.
【解答】
解:设路灯的高为x米,
∵GH⊥BD,AB⊥BD,
∴GH // AB.
∴△EGH∽△EAB.
∴GHx=EHEB①;
同理△FGH∽△FCD,GHx=FHFD②.
∴EHEB=FHFD=EH+FHEB+FD,
∴3EB=3+1.512+3+1.5,
解得EB=11米,
∴ 1.8x=311,
解得x=6.6.
故答案为 6.6.
14.【答案】6.6
【解析】解:设路灯的高为x米,
∵GH⊥BD,AB⊥BD,
∴GH//AB.
∴△EGH∽△EAB.
∴GHx=EHEB①.
同理△FGH∽△FCDGHx=FHFD②.
∴EHEB=FHFD=EH+FHEB+FD.
∴3EB=4.512+4.5.
解得EB=11米,代入①得1.8x=311,
解得x=6.6.
故答案为:6.6.
利用相似三角形的相似比,列出方程,通过解方程求出路灯的高即可.
本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求出路灯的高,体现了转化的思想.
15.【答案】514cm
【解析】解:如图,作BE⊥DE于E,则∠BED=90°,
由题意知,BD=17,BC=6,BE=8,∠C=90°,AB//DE,AC//BD,
∴∠CAB=∠DBA=∠BDE,
又∵∠C=∠BED=90°,
∴△CAB∽△EDB,
∴ABBD=BCBE,即AB17=68,
解得,AB=514,
故答案为:514cm.
如图,作BE⊥DE于E,则∠BED=90°,由题意知,BD=17,BC=6,BE=8,∠C=90°,AB//DE,AC//BD,则∠CAB=∠DBA=∠BDE,证明△CAB∽△EDB,则ABBD=BCBE,即AB17=68,计算求解即可.
本题考查了相似三角形的判定与性质,平行线的判定与性质.熟练掌握相似三角形的判定与性质是解题的关键.
16.【答案】14
【解析】解:∵DE⊥CE,AC⊥CE,
∴∠C=∠E=90°,
根据平面镜反射原理,入射角等于反射角可得:∠ABC=∠DBE,
∴△ABC∽△DBE,
∴DEAC=BEBC,即1.6AC=2.421,
解得:AC=14,
故答案为:14.
根据题意可得△ABC∽△DBE,根据相似三角形对应边成比例,即可进行解答.
本题主要考查了利用相似三角形测高,解题的关键是掌握相似三角形对应边成比例.
17.【答案】解:∵AB//MN,
∴∠PAB=∠PQC,∠PBA=∠PCQ,
∴△PAB∽△PQC,
∴PAPQ=ABCQ,
即PAPA+AQ=ABCQ,
∴PAPA+0.6=2.753,
解得:PA=6.6(m),
∴PQ=PA+AQ=66.6+0.6=7.2(m),
答:大树PQ的高度为7.2m.
【解析】由AB//MN,证得△PAB∽△PQC,得出PAPQ=ABCQ,求出PA=6.6m,即可得出答案.
本题考查了相似三角形的应用,熟练掌握相似三角形的判定与性质是解题的关键.
18.【答案】解:如图所示,过E作EG⊥BC于G,
∵DE//BC,
∴△ABC∽△ADE,
∴ACAE=BCDE=80140=47,
∴ACEC=43,
∵AF⊥BC,EG⊥BC,
∴∠CFA=∠CGE=90°,
∵∠ECG=∠ACF,
∵∠ECG=∠ACF,
∴△ACF∽△ECG,
∴AFEG=ACEC,即AF75=43,
解得:AF=100,
∴桥AF的长度为100米.
【解析】过E作EG⊥BC于G,依据△ABC∽△ADE,即可得出ACEC=43,依据△ACF∽△ECG,即可得到AFEG=ACEC,进而得出AF的长.
本题主要考查了利用相似测量距离.正确构造直角三角形相似是解题关键.
19.【答案】(1)解:图形如图所示:
(2)证明:∵AT平分∠DAB,AD=AB,
∴AD,AB关于AT对称,
∴ED=EB,
∵BD=DE=1,
∴EB=DB=1,
∵∠EAD=∠EAB,∠DAB=2∠BAC,
∴∠EAB=∠BAC,
∵AE=AC,
∴AE,AC关于AB对称,
∴BE=BC=1,
∵△ACE∽△ABD,
∴EC:BD=AC:AB= 2,
∴EC= 2,
∴BC2+BE2=1+1=2,EC2=2,
∴BE2+BC2=EC2,
∴∠EBC=90°,
【解析】(1)作AT平分∠DAB,在射线AT上截取AE,使得AE=AC,点E即为所求;
(2)利用勾股定理的逆定理判断即可.
本题考查作图−相似变换,勾股定理的逆定理等知识,解题的关键是掌握相似变换的性质,属于中考常考题型.
20.【答案】解:过点A作AH⊥EF,交CD于点G,交EF于点H.
由题意得:AG=BD=4米,HG=FD=40米,HF=DG=AB=1.6米,CG=CD−DG=3−1.6=1.4(米).
∵EF⊥BF,CD⊥BF,
∴EF//CD,
∴△AGC∽△AHE,
∴AGCG=AHHE,
∴41.4=4+40HE,
∴HE=15.4米,
∴EF=HE+HF=15.4+1.6=17(米).
答:旗杆EF的高度为17米.
【解析】本题主要考查了相似三角形的应用,能够熟练掌握相似三角形的判定与性质是解决本题的关键.
过点A作AH⊥EF,交CD于点G,交EF于点H,根据已知条件证明△AGC∽△AHE,列出比例式求出HE的长,再根据线段的和差关系即可求得旗杆EF的高度.
21.【答案】解:由题意得,∠OAB=∠CDF=∠EDB=90∘,∠OBA=∠EBD,∠CFD=∠OFA,
∴△OAB∽△EDB,△OAF∽△CDF,
∴OAED=ABDB,OACD=AFDF,
即OA1.5=1+AD1,OA1=AD+0.60.6,
解得OA=6.
∴路灯的点光源O到地面的高度OA为6m,
【解析】此题考查了相似三角形的应用,判定三角形相似是解题的关键,根据题意得出△OAB∽△EDB,△OAF∽△CDF,利用相似三角形的性质得出OAED=ABDB,OACD=AFDF,求出OA,即可得出结果,
22.【答案】解:由题意得:AB⊥BH,CD⊥BH,EF⊥BH,
∴∠ABH=∠CDH=∠EFH=90°,
∵∠CGD=∠AGB,
∴△CDG∽△ABG,
∴CDAB=DGBG,
∴20AB=8080+BD,
∵∠H=∠H,
∴△EHF∽△AHB,
∴EFAB=FHBH,
∴20AB=160160+200+BD,
∴8080+BD=160160+200+BD,
解得:BD=200,
∴20AB=8080+200,
解得:AB=70,
∴山峰的高度AB为70米,它和标杆CD的水平距离BD是200米.
【解析】【分析】根据题意可得:AB⊥BH,CD⊥BH,EF⊥BH,从而可得∠ABH=∠CDH=∠EFH=90°,然后证明A字模型相似△CDG∽△ABG,△EHF∽△AHB,从而利用相似三角形的性质进行计算,即可解答.
【点评】本题考查了相似三角形的应用,熟练掌握A字模型相似三角形是解题的关键.
23.【答案】【详解】(1)解:∵EF//CD,
∴▵GFE∽▵GDC,
∴GEGC=EFCD,
∵GE=6m,EF=1.5m,CD=10m,
∴66+EC=1.510,
解得,EC=34m,
答:此时小凯到路灯CD的距离EC=34m;
(2)解:如图,
由(1)可得:EHHA=GEGC=EFCD=1.510=320,
∴HEAE=GECE,
又∠GEH=∠CEA,
∴▵GHE∽▵CEA,
∴∠ACE=∠HGE
∴GH//AC;
(3)解:如图,
同(2)可得▵GHE∽▵CEA,
∴GHAC=GEEC,
∵GH=9m,CE=34m,AC=40m,
∴940=GE34,
∴GE=15320m,
又▵GFE∽▵GDC
∴GEGC=FECD,
∴1532015320+34=EF10
解得,EF=9049m,
所以,小凯头顶离地面的最大高度9049m.
【解析】【分析】本题主要考查相似三角形的判定与性质:
(1)证明▵GFE∽▵GDC,运用相似三角形的性质即可得出结论;
(2)证明▵GHE∽▵CEA,可得∠ACE=∠HGE,可得GH//AC;
(3)由▵GHE∽▵CEA,求出GE,再由▵GFE∽▵GDC求出EF即可
24.【答案】解:(1)∵AO⊥BC,BC=6,
∴BE=12BC=3,
∵OB=5,
∴OE= OB2−BE2= 52−32=4,
∴AE=AO+OE=5+4=9,
∴AB= AE2+BE2= 92+32=3 10.
(2)如图,延长线段BO交AD于点F,过点F作FM⊥CD,
∵AF//BE,
∴△AOF∽△EOB,
∴AOEO=AFBE,
∴54=AF3,
∴AF=154,
∴FD=AD−AF=6−154=94,
∵∠D=∠ABE,∠AEB=∠FMD,
∴△ABE∽△FDM,
∴AEFM=ABFD,
∴9FM=3 1094,
∴FM=27 1040.
【解析】(1)由AO⊥BC,BC=6,得出BE=12BC=3,再根据勾股定理即可得出OE的长度,进而得出答案;
(2)延长线段BO交AD于点F,过点F作FM⊥CD,得出△AOF∽△EOB,再得出AOEO=AFBE,即可得出AF与FD的长度,再根据∠D=∠ABE,∠AEB=∠FMD得出△ABE∽△FDM,进而求出答案.
本题主要考查相似三角形的应用,勾股定理,垂径定理,熟练掌握以上知识点是解题的关键.
25.【答案】解:(1)如图,点D即为所求作的点;
(2)连接AM、AN,
∵M,N分别是BD,BC的中点,
∴AM、AN分别是△ABD,△ABC的中线,
∵△ABD∽△ACB,
∴ADAB=ABAC=AMAN,
∴1AB=AB4,
∴AB=2,
∴AMAN=12.
【解析】(1)利用尺规作图作∠ABD=∠C即可;
(2)由M,N分别是BD,BC的中点知AM、AN分别是△ABD,△ABC的中线,根据相似三角形的性质可得ADAB=ABAC=AMAN,代入计算即可.
本题主要考查作图—相似变换,解题的关键是掌握相似三角形的判定与性质.
数学九年级上册4.5 相似三角形的性质及应用练习题: 这是一份数学九年级上册4.5 相似三角形的性质及应用练习题,共10页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
九年级上册4.5 相似三角形的性质及应用精品巩固练习: 这是一份九年级上册4.5 相似三角形的性质及应用精品巩固练习,共19页。
初中数学浙教版九年级上册4.3 相似三角形精品精练: 这是一份初中数学浙教版九年级上册4.3 相似三角形精品精练,共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













