浙教版九年级上册4.6 相似多边形优秀练习题

这是一份浙教版九年级上册4.6 相似多边形优秀练习题，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.已知两个相似多边形的面积比是9:16，其中较小多边形的周长为36 cm，则较大多边形的周长为( )
A. 48 cmB. 54 cmC. 56 cmD. 64 cm
2.如果两个相似多边形的周长比是2：3，那么它们的面积比为( )
A. 2：3B. 4：9C. 2： 3D. 16：81
3.若两个相似多边形的相似比为1：2，则它们周长的比为( )
A. 1：1B. 1：2C. 1：3D. 1：4
4.如图，点O为四边形ABCD内的一点，连结OA，OB，OC，OD，若OA′OA=OB′OB=OC′OC=OD′OD=14，则四边形A′B′C′D′的面积与四边形ABCD的面积比为( )
A. 1:2B. 1:4C. 1:8D. 1:16
5.如图所示，在长为8cm，宽为6cm的矩形中，截去一个矩形(图中阴影部分)，如果剩下的矩形与原矩形相似，那么剩下矩形的面积是( )
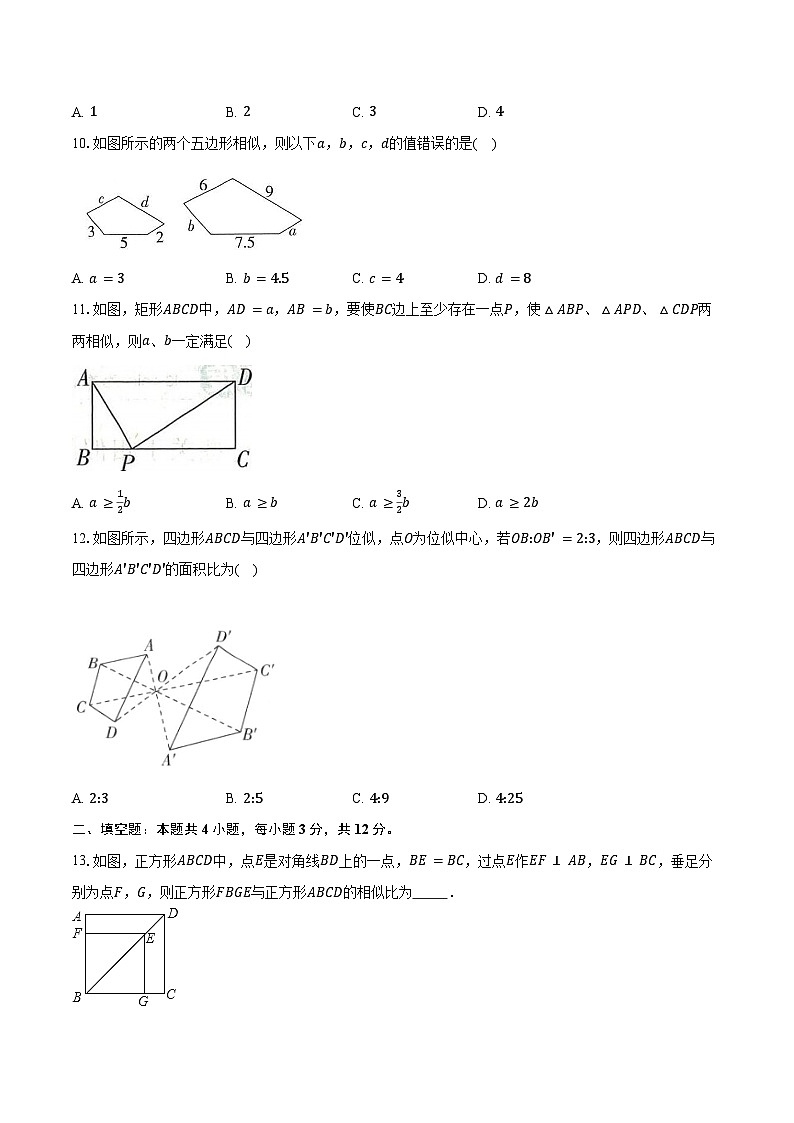
A. 28cm2B. 27cm2C. 21cm2D. 20cm2
6.如图，四边形ABCD∽四边形EFGH，则下列角的度数正确的是( )
A. ∠D=81°B. ∠F=83°C. ∠G=78°D. ∠H=76°
7.如图，矩形相框的外框矩形的长为12dm，宽为8dm，上下边框的宽度都为x dm，左右边框的宽度都为y dm，则符合下列条件的x，y的值能使内框矩形和外框矩形相似的为( )
A. x=yB. 3x=2yC. x=1，y=2D. x=3，y=2
8.如图1是古希腊时期的巴台农神庙(PartℎenmTemple)，把图1中用虚线表示的矩形画成图2矩形ABCD，当以矩形ABCD的宽AB为边作正方形ABEF时，惊奇地发现矩形CDFE与矩形ABCD相似，则BEEC等于( )
A. 5−12B. 32C. 3+12D. 5+12
9.如图，在平面直角坐标系中，矩形OABC∽矩形OA′B′C′，B′(10,5)，AA′=1，则CC′的长是( )
A. 1B. 2C. 3D. 4
10.如图所示的两个五边形相似，则以下a，b，c，d的值错误的是( )
A. a=3B. b=4.5C. c=4D. d=8
11.如图，矩形ABCD中，AD=a，AB=b，要使BC边上至少存在一点P，使△ABP、△APD、△CDP两两相似，则a、b一定满足( )
A. a≥12bB. a≥bC. a≥32bD. a≥2b
12.如图所示，四边形ABCD与四边形A′B′C′D′位似，点O为位似中心，若OB:OB′=2:3，则四边形ABCD与四边形A′B′C′D′的面积比为( )
A. 2:3B. 2:5C. 4:9D. 4:25
二、填空题：本题共4小题，每小题3分，共12分。
13.如图，正方形ABCD中，点E是对角线BD上的一点，BE=BC，过点E作EF⊥AB，EG⊥BC，垂足分别为点F，G，则正方形FBGE与正方形ABCD的相似比为 ．
14.如图，已知矩形ABCD∽矩形BCFE，AE=4，EB=1，则BC的长为______．
15.将一张长方形纸片对折，若得到的小长方形与原长方形相似，则原长方形的长与宽的比是________________．
16.如图，BD为四边形ABCD的对角线，E是AB的中点，DA⊥AB，CB⊥AB，AB=BC=2AD，连接CE交BD于点F.若DF=3，则AB的长为________．
三、解答题：本题共9小题，共72分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题8分)
如图，▱ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F．
(1)求证：▱ABEF是菱形：
(2)若▱ABCD∽▱FDCE，则BCCD的值为______．
18.(本小题8分)
如图，点E是菱形ABCD对角线CA的延长线上任意一点，以线段AE为边作一个菱形AEFG，且菱形AEFG∽菱形ABCD，相似比是 3:2，连接EB，GD．
(1)求证：EB=GD．
(2)若∠DAB=60∘，AB=2，求GD的长．
19.(本小题8分)
如圖，四邊形EFGH與四邊形KNML相似，求∠E、∠G、∠N的度數以及x、y、z的值．
20.(本小题8分)
如图，四边形ABCD与四边形AˈBˈCˈDˈ相似．
(1) α= ，四边形ABCD与四边形AˈBˈCˈDˈ的相似比为 ；
(2)求x，y的值．
21.(本小题8分)
根据相似多边形的定义，我们把四个角分别相等，四条边成比例的两个凸四边形叫做相似四边形．相似四边形对应边的比叫做相似比．
(1)某同学在探究相似四边形的判定时，得到如下三个命题，请判断它们是否正确(直接在横线上填写“真”或“假”)．
①四条边成比例的两个凸四边形相似；(______命题)
②三个角分别相等的两个凸四边形相似；(______命题)
③两个大小不同的正方形相似．(______命题)
(2)如图1，在四边形ABCD和四边形A1B1C1D1中，∠ABC=∠A1B1C1，∠BCD=∠B1C1D1，ABA1B1=BCB1C1=CDC1D1.求证：四边形ABCD与四边形A1B1C1D1相似．
(3)如图2，四边形ABCD中，AB/​/CD，AC与BD相交于点O，过点O作EF/​/AB分别交AD，BC于点E，F.记四边形ABFE的面积为S1，四边形EFCD的面积为S2，若四边形ABFE与四边形EFCD相似，求S2S1的值．
22.(本小题8分)
如图，梯形ABCD中，AD/​/BC，E是AB上的一点，EF/​/BC，并且EF将梯形ABCD分成的两个梯形AEFD、EBCF相似，若AD=9，BC=16，求AE:EB．
23.(本小题8分)
几何体的三视图相互关联.已知直三棱柱的三视图如图所示，在△PMN中，∠MPN=90∘，PN=4，sin∠PMN=45．
(1)求BC及FG的长;
(2)若主视图与左视图两矩形相似，求AB的长;
(3)在(2)的情况下，求直三棱柱的表面积．
24.(本小题8分)
已知四边形ABCD与四边形A1B1C1D1相似，并且点A与点A1、点B与点B1、点C与点C1、点D与点D1对应．
(1)已知∠A=40°，∠B=110°，∠C1=90°，求∠D的度数；
(2)已知AB=9，CD=15，A1B1=6，A1D1=4，B1C1=8，求四边形ABCD的周长．
25.(本小题8分)
如图，E是菱形ABCD的对角线CA的延长线上任意一点，以线段AE为边作一个菱形AEFG，且菱形AEFG∽菱形ABCD，连接EB、GD．
(1)求证：EB=GD;
(2)若∠DAB=60∘，AB=2，AG= 3，求GD的长．
答案和解析
1.【答案】A
【解析】【分析】
本题考查相似多边形的性质．相似多边形对应边之比、周长之比等于相似比，面积之比等于相似比的平方．
根据相似多边形对应边之比、周长之比等于相似比，而面积之比等于相似比的平方计算即可．
【解答】
解：两个相似多边形的面积比是9：16，面积比是相似比的平方，
∴较大多边形与较小多边形的相似比是4：3．
∴相似多边形周长的比等于相似比，为4：3．
设较大多边形的周长为xcm，
则有x36=43，
解得：x=48．
即较大多边形的周长为48cm．
故选A．
2.【答案】B
【解析】【分析】
本题考查相似多边形的性质，掌握相似多边形的周长比等于相似比，面积比等于相似比的平方是解题的关键．
直接根据相似多边形的性质即可得出结论.
【解答】
解：∵两个相似多边形的周长比是2:3，
∴两个相似多边形的相似比是2:3，
∴它们的面积比是4:9．
故选B．
3.【答案】B
【解析】解：∵两个相似多边形的相似比为1：2，
∴两个相似多边形周长的比等于1：2，
故选：B．
直接根据相似多边形周长的比等于相似比进行解答即可．
本题考查的是相似多边形的性质，即相似多边形周长的比等于相似比．
4.【答案】D
【解析】【分析】
本题主要考查了相似多边形的性质.根据题意得出两四边形的相似比是解题关键．
利用位似图形的定义得出四边形A′B′C′D′与四边形ABCD的位似比为1：4，进而得出面积比．
【解答】
解：∵OA′OA=OB′OB=OC′OC=OD′OD=14，
∴四边形A′B′C′D′与四边形ABCD的位似比为1：4，
∴四边形A′B′C′D′与四边形ABCD的面积比为1：16．
5.【答案】B
【解析】【分析】
本题就是考查相似形的对应边的比相等，分清矩形的对应边是解决本题的关键．
根据题意，剩下矩形与原矩形相似，利用相似形的对应边的比相等可得．
【解答】
解：依题意，在矩形ABDC中截取矩形ABFE，
则矩形ABDC∽矩形FDCE，
则ABDF=BDDC，
设DF=xcm，得到：
6x=86，解得：x=4.5，
则剩下的矩形面积是：4.5×6=27cm2．
故选：B．
6.【答案】D
【解析】解：∵四边形ABCD和四边形EFGH相似，
∴∠B=∠F=78°，∠A=∠E=118°，∠C=∠G=88°，
∴∠D=∠H=360°−78°−118°−88°=76°．
故选：D．
直接利用相似多边形的性质得出对应角相等进而得出答案．
此题主要考查了相似多边形的性质，正确得出对应角相等是解题关键．
7.【答案】B
【解析】如图，当矩形ABCD∽矩形EFGH时，则有ABEF=ADEH，∴88−2x=1212−2y，可得3x=2y，选项B符合题意.当矩形ABCD∽矩形EHGF时，则有ABEH=ADEF，∴812−2y=128−2x，可得2x−3y+10=0.综上，只有B选项符合题意，故选B．
8.【答案】D
【解析】解：∵四边形ABEF是正方形，
∴BE=AB，
∵四边形ABCD是矩形，
∴AB=CD，
∴BE=CD，
∵矩形CDFE与矩形ABCD相似，
∴ABBC=CECD，
∴BEBC=CEBE，
∴点E是BC的黄金分割点，
∴CEBE= 5−12，
∴BECE=2 5−1= 5+12，
故选：D．
根据正方形的性质可得BE=AB，再根据矩形的性质可得AB=CD，从而可得BE=CD，然后利用相似多边形的性质可得ABBC=CECD，从而可得BEBC=CEBE，进而可得点E是BC的黄金分割点，然后根据黄金分割的定义可得CEBE= 5−12，从而进行计算即可解答．
本题考查了相似多边形的性质，矩形的性质，正方形的性质，黄金分割，熟练掌握相似多边形的性质，以及黄金分割的定义是解题的关键．
9.【答案】B
【解析】∵点B′的坐标为(10,5)，四边形OABC和四边形OA′B′C′是矩形，∴B′C′=OA′=5，A′B′=OC′=10，AO=BC．∵AA′=1，∴AO=BC=A′O−AA′=4．∵矩形OABC∽矩形OA′B′C′，∴OCOC′=BCB′C′，即OC10=45，∴OC=8，∴CC′=OC′−OC=10−8=2，故选B．
10.【答案】D
【解析】∵两个五边形相似，
∴2a=3b=c6=d9=57.5，
∴a=3，b=4.5，c=4，d=6.故选D．
11.【答案】D
【解析】设PC=x，则BP=a−x．
∵△ABP∽△PCD，
∴ABPC=BPCD，即bx=a−xb，即x2−ax+b2=0，
方程有解的条件是a2−4b2≥0，
∴(a+2b)(a−2b)≥0，则a−2b≥0，
∴a≥2b.故选D．
12.【答案】C
【解析】∵四边形ABCD与四边形A′B′C′D′位似，
∴四边形ABCD∽四边形A′B′C′D′，AB//A′B′，
∴△OAB∽△OA′B′，
∴ABA′B′=OBOB′=23，
∴四边形ABCD与四边形A′B′C′D′的面积比=(ABA′B′)2=49，
故选C．
13.【答案】 2：2
【解析】【分析】
本题主要考查相似多边形的性质，解题的关键是掌握正方形的性质和相似多边形的性质．
设BG=x，根据正方形的性质知BE=BC= 2x，由正方形FBGE与正方形ABCD的相似比=BG：BC可得答案．
【解答】
解：设BG=x，
则BE= 2x，
∵BE=BC，
∴BC= 2x，
则正方形FBGE与正方形ABCD的相似比=BGBC=x 2x= 22．
故答案为： 22．
14.【答案】 5
【解析】解∵四边形ABCD和四边形BCFE都是矩形，
∴AD=BC，EF=BC，
∴AD=EF=BC，
∵AE=4，EB=1，
∴AB=AE+BE=5，
∵矩形ABCD∽矩形BCFE，
∴ABBC=ADBE，即5BC=BC1，
∴BC= 5(负值舍去)，
经检验，BC= 5是原方程的解，
故答案为： 5．
先根据矩形的性质得到AD=EF=BC，再求出AB=AE+BE=5，最后根据相似多边形对应边成比例得到ABBC=ADBE，据此代值计算即可．
本题主要考查了相似多边形的性质，矩形的性质，解题的关键是掌握相似多边形的性质．
15.【答案】 2：1
【解析】【分析】设AE=ED=a，AB=b，根据每一个小长方形与原长方形相似，可知ab=b2a，再由a，b均为正数可知b= 2a，由此即可得出结论．
【解答】解：设AE=ED=a，AB=b，
∵每一个小长方形与原长方形相似，
∴ab=b2a，
∴b2=2a2，
∵a，b均为正数，
∴b= 2a，
∴ADAB=2ab=2a 2a= 2，
∴原长方形的长与宽之比为 2：1．
故答案为： 2：1．
16.【答案】2 5
【解析】【分析】
本题考查三角形的中位线、相似三角形和勾股定理求线段长度，取BD的中点G，连接EG，可得EG=12AD=14BC，EG//AD//BC，根据相似比可得GF=14BF，求得FG=12，BF=2，CF=4，BC=2 5．
【解答】
解：取BD的中点G，连接EG，
∵E是AB的中点，
∴EG//AD，EG=12AD，
∵BC=2AD，
∴BC=4EG，
∵DA⊥AB，CB⊥AB，
∴∠DAB=∠EBC=90°，
∴AD//CB//GE，
∴FGFB=EGBC=14，
∴BF=4FG，
∴BG=BF+FG=5FG，
∵G是BD中点，
∴DG=BG=5FG，
∵DF=3，
∴DF=DG+GF=6FG=3，
∴GF=0.5，BF=2，
∵∠ABD+∠CBD=∠ABD+∠ADB=90°，
∴∠CBD=∠ADB，
∵AB=BC，
∴△ABD≌△BCE，
∴∠ABD=∠BCE，
∴∠BCE+∠CBF=∠ABD+∠CBF=90°，
∴∠CFB=90°，即BF⊥CE，
∵E是AB的中点，
∴BE=12AB=12BC，
∴CE= BE2+BC2= 5BE，
∵BEⅹBC=CE⨉BF，
∴2BE2=2 5BE，
∴BE= 5，
∴AB=2 5．
17.【答案】【详解】(1)∵∠BAD的平分线交BC于点E，
∴∠BAE=∠EAF．
∵四边形ABCD是平行四边形，
∴AD//BC．
∴∠EAF=∠AEB．
∴∠BAE=∠AEB．
∴AB=BE．
同理，AB=AF．
∴BE=AF．
∵AD//BC
∴四边形ABEF是平行四边形．
∵AB=BE，
∴四边形ABEF是菱形．
(2)由(1)知，四边形ABEF是菱形，
∴AB=BE=EF=FA,
又四边形CDFE是平行四边形，
∴FD=CE,EF=CD，
∴AB=BE=EF=FA=CD,
设FD=CE=x，AF=BE=CD=y，则有：BC=BE+CE=x+y,
∵▱ABCD∼▱FDCE,
∴ADCD=CDFD，即x+yy=yx，
整理得，x2+xy−y2=0.
解得，x=−1± 52y,
∵x>0
∴x= 5−12y，
∴BCCD=x+yy= 5+12yy = 5+12，
故答案为：1+ 52

【解析】【分析】(1)根据平行四边形的性质和菱形的判定解答即可；
(2)根据菱形的性质和平行四边形的性质可以得到AB=BE=EF=FA=CD,设FD=x,CD=y，根据相似多边形的性质可得ADCD=CDFD，列方程求出x和y的关系，从而可解答本题
本题主要考查了菱形的判定与性质、平行四边形的性质以及相似多边形的性质，求出AF与FD的数量关系是解答本题的关键
18.【答案】【小题1】
证明：∵菱形AEFG∽菱形ABCD，∴∠EAG=∠BAD，AE=AG，AB=AD，∴∠EAG+∠GAB=∠BAD+∠GAB，∴∠EAB=∠GAD．∵AE=AG，AB=AD，∴△AEB≌△AGD，∴EB=GD．
【小题2】
如图，连接BD交AC于点P，则BP⊥AC．
∵∠DAB=60∘，∴∠PAB=30∘．
∵菱形AEFG∽菱形ABCD，相似比是 3:2，AB=2，∴AE= 3，BP=12AB=1，∴AP= AB2−BP2= 3，∴EP=AE+AP=2 3，
∴EB= EP2+BP2= 12+1= 13，
∴GD= 13．

【解析】1. 见答案
2. 见答案
19.【答案】解：∵四边形EFGH相似于四边形KNML，
∴∠E=∠K=67°，∠G=∠M=107°，∠N=∠F=43°，
∵四边形EFGH相似于四边形KNML，
∴x35=9y=12z=610，
解得x=21，y=15，z=20．

【解析】观察图形，可知两个相似的四边形的四个角中有两个锐角，两个钝角，根据相似多边形的对应角相等得出∠E=∠K=67°，∠G=∠M=107°，∠N=∠F=43°，再根据相似多边形对应边成比例列出比例式比即可求得x，y，z．
本题考查了相似多边形的性质：①对应角相等；②对应边的比相等．准确识图，找准对应顶点是解题的关键．
20.【答案】【小题1】
83°
32
【小题2】
∵四边形ABCD与四边形AˈBˈCˈDˈ相似，∴x9=y13=32，解得x=272，y=392

【解析】1.
∵四边形ABCD与四边形AˈBˈCˈDˈ相似，∴∠Aˈ=∠A=62°，∠Bˈ=∠B=75°.∴∠Cˈ=360°−62°−75°−140°=83°.四边形ABCD与四边形AˈBˈCˈDˈ的相似比为96=32．
2. 见答案
21.【答案】解：(1)假，假，真．
(2)证明：如图1中，连接BD，B1D1．
∵∠BCD=∠B1C1D1，且BCB1C1=CDC1D1，
∴△BCD∽△B1C1D1，
∴∠CDB=∠C1D1B1，∠C1B1D1=∠CBD，
∵ABA1B1=BCB1C1=CDC1D1，
∴BDB1D1=ABA1B1，
∵∠ABC=∠A1B1C1，
∴∠ABD=∠A1B1D1，
∴△ABD∽△A1B1D1，
∴ADA1D1=ABA1B1，∠A=∠A1，∠ADB=∠A1D1B1，
∴ABA1B1=BCB1C1=CDC1D1=ADA1D1，∠ADC=∠A1D1C1，∠A=∠A1，∠ABC=∠A1B1C1，∠BCD=∠B1C1D1，
∴四边形ABCD与四边形A1B1C1D1相似．
(3)如图2中，
∵四边形ABCD与四边形EFCD相似．
∴DEAE=EFAB，
∵EF=OE+OF，
∴DEAE=OE+OFAB，
∵EF/​/AB/​/CD，
∴DEAD=OEAB，DEAD=OCAC=OFAB，
∴DEAD+DEAD=OEAB+OFAB，
∴2DEAD=DEAE，
∵AD=DE+AE，
∴2DE+AE=1AE，
∴2AE=DE+AE，
∴AE=DE，
∵S2S1=DE2AE2，
∴S2S1=1．
【解析】【分析】
(1)根据相似多边形的定义即可判断．
(2)根据相似多边形的定义证明四边成比例，四个角相等即可．
(3)四边形ABFE与四边形EFCD相似，证明相似比是1即可解决问题，即证明DE=AE即可．
本题属于相似形综合题，考查了相似三角形的判定和性质，相似多边形的判定和性质等知识，解题的关键是学会用转化的思想思考问题，属于中考压轴题．
【解答】
(1)解：①四条边成比例的两个凸四边形相似，是假命题，角不一定相等．
②三个角分别相等的两个凸四边形相似，是假命题，边不一定成比例．
③两个大小不同的正方形相似．是真命题．
故答案为假，假，真．
(2)(3)见答案．
22.【答案】解：梯形AEFD∽梯形EBCF，
∴ADEF=EFBC=AEEB，
又∵AD=9，BC=16，
∴EF2=AD⋅BC=9×16=144，
∵EF>0，
∴EF=12，
∴AEEB=ADEF=912=34，即AE:EB=3:4．
【解析】本题考查了相似多边形的性质，相似多边形的对应边的比相等．梯形AEFD、EBCF相似，AE与EB是相似梯形的对应边，根据相似多边形的对应边成比例，因而可以把求AE：EB转化为求AD：EF．
23.【答案】解：(1)由图可知：BC=MN，FG=PM，
∵sin∠PMN=PNMN=45，PN=4，
∴MN=5，PM=3，
∴BC=5，
∵12PM⋅PN=12ℎ⋅MN
∴ℎ=125
∴FG=125；
(2)∵矩形ABCD与矩形EFGH相似，且AB=EF，
∴ABFG=BCEF，
即AB125=5AB，
∴AB= 12=2 3；
(3)直三棱柱的表面积：12×3×4+5×2 3+3×2 3+4×2 3=12+24 3．

【解析】本题主要考查立体图形的三视图，锐角三角函数，相似多边形的性质以及立体图形的表面积.从三视图入手，找出边之间的关系，利用三角函数解决问题．
(1)由图可知BC=MN，FG=PM，进一步由锐角三角函数的意义与勾股定理求得答案即可；
(2)利用相似的性质列出比例式，代入数值求得答案即可；
(3)求出五个面的面积和得出答案即可．
24.【答案】解：(1)∵四边形ABCD与四边形A1B1C1D1相似，
∴∠C=∠C1=90°，
∴∠D=360°−∠A−∠B−∠C=360°−40°−110°−90°=120°．
(2)∵四边形ABCD与四边形A1B1C1D1相似，
∴ABA1B1=BCB1C1=ADA1D1，
∴96=BC8=AD4，
∴BC=12，AD=6，
∴四边形ABCD的周长=AB+BC+CD+AD=9+12+15+6=42．
【解析】(1)根据相似多边形的对应角相等解决问题即可．
(2)根据相似多边形的对应边成比例，解决问题即可．
本题考查相似多边形的性质，解题的关键是掌握相似多边形的对应角相等，对应边成比例．
25.【答案】(1)证明：∵菱形AEFG∽菱形ABCD，
∴∠EAG=∠BAD.
∴∠EAG+∠GAB=∠BAD+∠GAB，即∠EAB=∠GAD.
∵AE=AG，AB=AD，
∴△AEB≌△AGD．
∴EB=GD．
(2)解：连接BD，交AC于点P，则BP⊥AC．
∵∠DAB=60∘，
∴∠PAB=30∘．
∴BP=12AB= 1．
∴AP= AB2−BP2= 3．
∵AE=AG= 3，
∴EP=2 3．
∴EB= EP2+BP2= 12+1= 13．
∴GD=EB= 13．

【解析】见答案