初中数学沪科版七年级下册第6章 实数6.2 实数课前预习ppt课件

这是一份初中数学沪科版七年级下册第6章 实数6.2 实数课前预习ppt课件，共25页。PPT课件主要包含了回顾与思考，实数与数轴上的点，这可以说明，反过来还可以说明，方法总结，练一练，总结归纳，b+a，abc，实数的运算等内容，欢迎下载使用。
下列各数中，哪些是有理数，哪些是无理数？
是有理数， 是无理数.
思考：有理数可以做加、减、乘、除、乘方运算，实数可以吗？
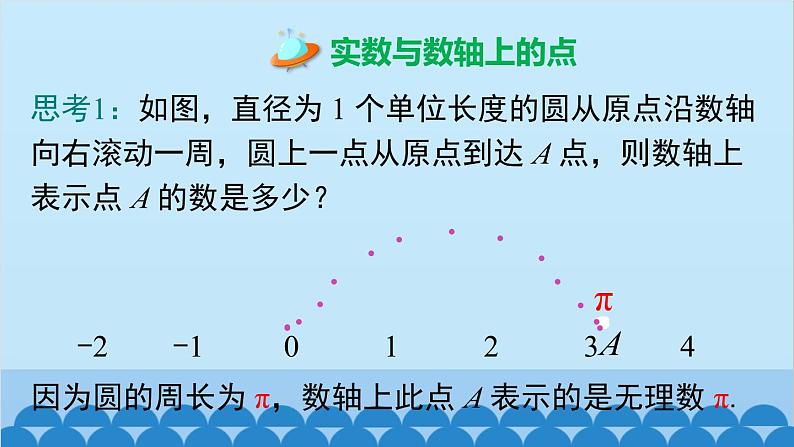
思考1：如图，直径为 1 个单位长度的圆从原点沿数轴向右滚动一周，圆上一点从原点到达 A 点，则数轴上表示点 A 的数是多少？
因为圆的周长为 π，数轴上此点 A 表示的是无理数 π.
思考2：如图，以数轴上的单位长度为边作一个正方形，以原点为圆心、这个正方形对角线的长为半径画弧，与数轴正半轴的交点记作 A，那么，点 A 表示什么数?
点 A′ 是画弧时与数轴的另一交点，它表示什么数？
推广：由上可知，无理数和有理数一样也可以用数轴上的点来表示.
每一个实数都可以用数轴上唯一的一个点来表示.
数轴上每一个点都表示唯一的一个实数.
上面两个结论结合起来可以简洁地说成：
实数和数轴上的点一一对应.
如果在数轴上表示正实数、零、负实数，它们分别应该在数轴上的什么位置呢？
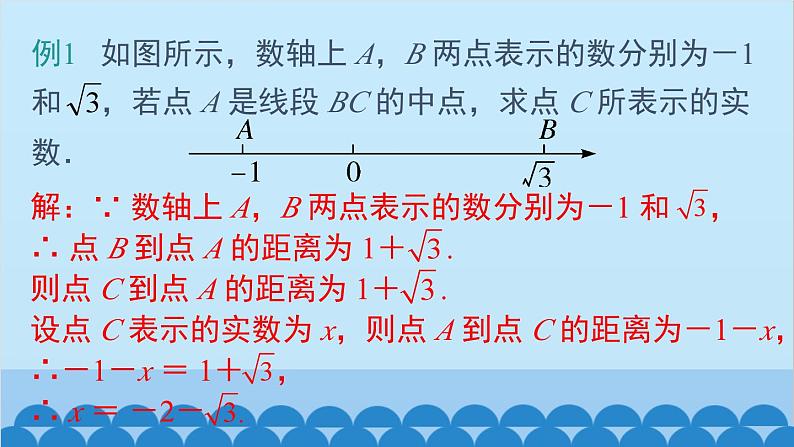
例1 如图所示，数轴上 A，B 两点表示的数分别为－1 和 ，若点 A 是线段 BC 的中点，求点 C 所表示的实数．
解：∵ 数轴上 A，B 两点表示的数分别为－1 和 ，∴ 点 B 到点 A 的距离为 1＋ .则点 C 到点 A 的距离为 1＋ .设点 C 表示的实数为 x，则点 A 到点 C 的距离为－1－x，∴－1－x ＝ 1＋ ，∴ x ＝ －2－
本题主要考查了实数与数轴之间的对应关系，其中利用了：当点 A 是线段 BC 的中点时，点 C 到点 A 的距离等于点 B 到点 A 的距离；两点之间的距离为两数差的绝对值．
例2 如图所示，数轴上 A，B 两点表示的数分别为 和 5.1，则 A，B 两点之间表示整数的点共有 ( )A．6 个 B．5 个 C．4 个 D．3 个
解析：∵ ≈ 1.414，∴ 和 5.1 之间的整数有 2，3，4，5，∴ A，B 两点之间表示整数的点共有 4 个.
例3 分别求下列各数的相反数、倒数和绝对值．
解：(1)∵ ＝－4，∴ 的相反数是 4，倒数是 ，绝对值是 4.(2) ∵ ＝15，∴ 的相反数是－15，倒数是 ，绝对值是 15.(3) 的相反数是－ ，倒数是 ，绝对值是 .
1. 的相反数是 ， 的相反数是 ， 的相反数是 .
2. -π 的绝对值是 ， = ， = .
1. 若 a 是一个实数，则实数 a 的相反数为 -a.
2. ① 一个正实数的绝对值是它本身； ② 一个负实数的绝对值是它的相反数； ③ 0 的绝对值是 0.
解：因为所以， 的相反数分别为由绝对值的意义得：
填空：设 a，b，c 是任意实数，则
（1）a + b = （加法交换律）；
（2）(a + b) + c = （加法结合律）；
（3）a + 0 = 0 + a = ；
（4）a + (-a) = (-a) + a = ；
（5）ab = （乘法交换律）；
（6）(ab)c = （乘法结合律）；
a + (b + c)
（7） 1 · a = a · 1 = ；
（8）a(b + c) = （乘法对于加法的分配律）， (b + c)a = （乘法对于加法的分配律）；
（9）实数的减法运算规定为 a - b = a + ；
（10）对于每一个非零实数 a，存在一个实数 b，满足 a · b = b · a = 1，我们把 b 叫做 a 的＿＿＿；
（11）实数的除法运算（除数 b≠0），规定为 a÷b = a · ；
（12）实数有一条重要性质：如果 a≠0，b≠0，那么 ab＿＿0.
每个正实数有且只有两个平方根，它们互为相反数. 0 的平方根是 0.
在实数范围内，负数没有平方根.
在实数范围内，每个实数有且只有一个立方根，而且与它本身的符号相同.
实数的平方根与立方根的性质：
此外，前面所学的有关数、式、方程（组）的性质、法则和解法，对于实数仍然成立.
例5 计算（结果保留小数点后两位）：
【方法总结】在实数运算中，如果遇到无理数，并且需要求出结果的近似值时，可按要求的精确度用相应的近似有限小数代替无理数，再进行计算.
显示：3.162 277 66.
精确到小数点后面第二位得：3.16.
在实数范围内，相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样．例如：
与 互为相反数；
思考：实数怎么比较大小呢？
与有理数规定的大小一样，数轴上右边的点表示的实数比左边的点表示的实数大.
1. 正数大于零，负数小于零，正数大于负数；2. 两个正数，绝对值大的数较大；3. 两个负数，绝对值大的数反而小.
与有理数一样，在实数范围内：
例7 在数轴上表示下列各点，比较它们的大小，并用 “ < ”连接它们.
熟记常见数的算术平方根的约数值有助于解题.
（3） 的相反数是______，绝对值是______.
（1）3.14 的相反数是_______，绝对值是_______；
（2） 的相反数是______，绝对值是______；
3. 用计算器计算（精确到 0.01）：
（1） ； （2） ； （3） .