

2024年中考数学压轴题型(江苏专用)专题04 图形阴影部分面积(选择填空压轴题)(含解析)
展开通用的解题思路:
在求解图形中阴影部分面积的问题时,通常的解题思路如下:
1. 理解题目:首先,需要明确题目中给出的图形是什么,阴影部分是如何定义的,以及是否有其他相关信息。
2. 分析图形:分析图形的形状和性质,确定是否可以直接使用公式计算面积。例如,如果阴影部分是一个规则的几何形状(如三角形、矩形、圆形等),那么可以直接使用相应的面积公式进行计算。
3. 分割与组合:如果阴影部分不是一个规则的几何形状,可以考虑使用分割或组合的方法。将阴影部分分割成几个规则的几何形状,然后分别计算这些形状的面积,最后将它们相加得到阴影部分的面积。或者,如果阴影部分是由几个不规则形状组成的,可以尝试将它们组合成一个规则的几何形状,然后计算这个组合形状的面积。
4. 使用辅助线:在某些情况下,可以通过添加辅助线来简化问题。辅助线可以帮助我们更好地理解和分析图形的性质,从而更容易地找到解决问题的方法。
5.应用公式:在确定了如何计算阴影部分面积的方法后,应用相应的公式进行计算。这可能需要一些基本的数学知识和技巧,如代数、几何等。
6. 检查答案:最后,检查答案是否合理,是否符合题目的要求。如果可能的话,可以使用不同的方法重新计算一遍,以确保答案的正确性。
1.(2023·江苏连云港·中考真题)如图,矩形 SKIPIF 1 < 0 内接于 SKIPIF 1 < 0 ,分别以 SKIPIF 1 < 0 为直径向外作半圆.若 SKIPIF 1 < 0 ,则阴影部分的面积是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D.20
【答案】D
【分析】根据阴影部分面积为2个直径分别为 SKIPIF 1 < 0 的半圆的面积加上矩形的面积减去直径为矩形对角线长的圆的面积即可求解.
【详解】解:如图所示,连接 SKIPIF 1 < 0 ,
∵矩形 SKIPIF 1 < 0 内接于 SKIPIF 1 < 0 , SKIPIF 1 < 0
∴ SKIPIF 1 < 0
∴阴影部分的面积是 SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0 ,
故选:D.
【点睛】本题考查了勾股定理,矩形的性质,熟练掌握勾股定理是解题的关键.
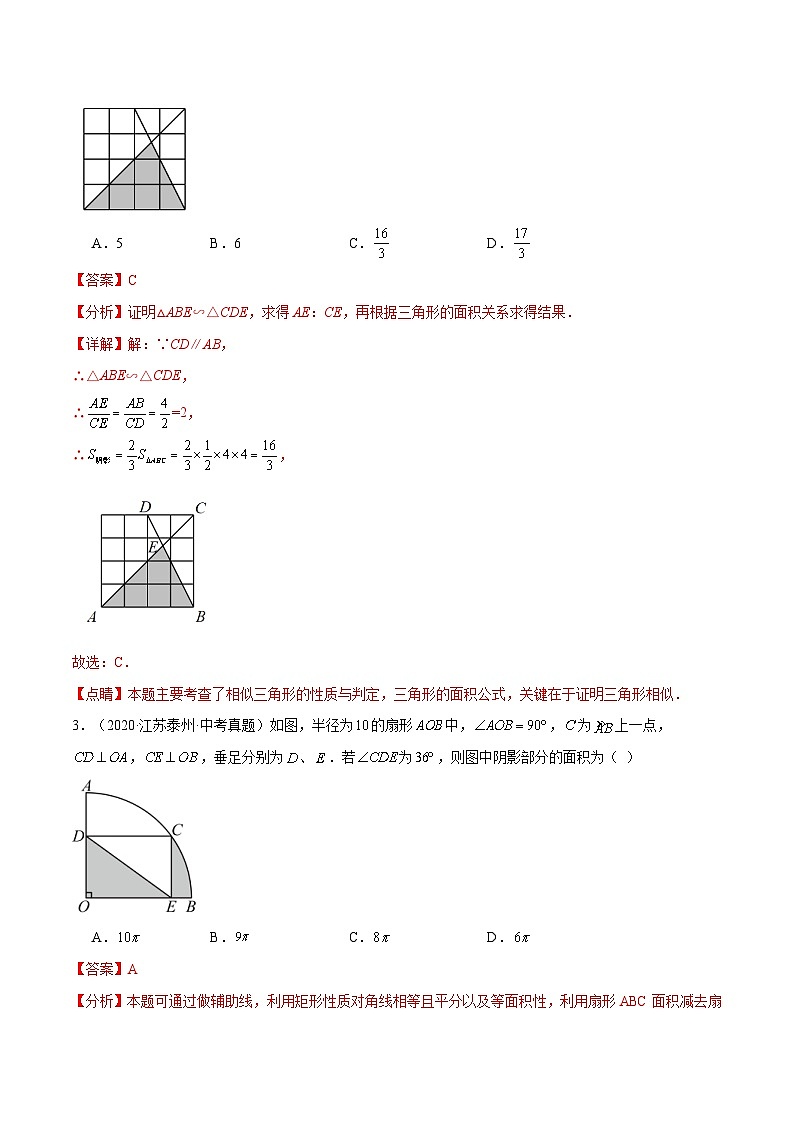
2.(2022·江苏徐州·中考真题)如图,若方格纸中每个小正方形的边长均为1,则阴影部分的面积为( )
A.5B.6C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
【答案】C
【分析】证明△ABE∽△CDE,求得AE:CE,再根据三角形的面积关系求得结果.
【详解】解:∵CD∥AB,
∴△ABE∽△CDE,
∴ SKIPIF 1 < 0 =2,
∴ SKIPIF 1 < 0 ,
故选:C.
【点睛】本题主要考查了相似三角形的性质与判定,三角形的面积公式,关键在于证明三角形相似.
3.(2020·江苏泰州·中考真题)如图,半径为 SKIPIF 1 < 0 的扇形 SKIPIF 1 < 0 中, SKIPIF 1 < 0 , SKIPIF 1 < 0 为 SKIPIF 1 < 0 上一点, SKIPIF 1 < 0 , SKIPIF 1 < 0 ,垂足分别为 SKIPIF 1 < 0 、 SKIPIF 1 < 0 .若 SKIPIF 1 < 0 为 SKIPIF 1 < 0 ,则图中阴影部分的面积为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
【答案】A
【分析】本题可通过做辅助线,利用矩形性质对角线相等且平分以及等面积性,利用扇形ABC面积减去扇形AOC面积求解本题.
【详解】连接OC交DE为F点,如下图所示:
由已知得:四边形DCEO为矩形.
∵∠CDE=36°,且FD=FO,
∴∠FOD=∠FDO=54°,△DCE面积等于△DCO面积.
SKIPIF 1 < 0 .
故选:A.
【点睛】本题考查几何面积求法,在扇形或圆形题目中,需要构造辅助线利用割补法,即大图形面积减去小图形面积求解题目,扇形面积公式为常用工具.
4.(2021·江苏徐州·中考真题)如图,四边形 SKIPIF 1 < 0 与 SKIPIF 1 < 0 均为矩形,点 SKIPIF 1 < 0 分别在线段 SKIPIF 1 < 0 上.若 SKIPIF 1 < 0 ,矩形 SKIPIF 1 < 0 的周长为 SKIPIF 1 < 0 ,则图中阴影部分的面积为 SKIPIF 1 < 0 .
【答案】 SKIPIF 1 < 0
【分析】根据矩形性质和矩形周长,得到 SKIPIF 1 < 0 ,然后设 SKIPIF 1 < 0 ,然后根据列出代数式 SKIPIF 1 < 0 即可求解阴影部分面积.
【详解】∵矩形 SKIPIF 1 < 0 的周长为 SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
设 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0 ,
故答案为 SKIPIF 1 < 0 .
【点睛】本题考查了矩形的性质,和列代数式及整式的化简,关键是读懂题目,列出代数式.
5.(2019·江苏苏州·中考真题)如图,一块含有 SKIPIF 1 < 0 角的直角三角板,外框的一条直角边长为 SKIPIF 1 < 0 ,三角板的外框线和与其平行的内框线之间的距离均为 SKIPIF 1 < 0 ,则图中阴影部分的面积为 SKIPIF 1 < 0 (结果保留根号)
【答案】 SKIPIF 1 < 0
【分析】过顶点A作AB⊥大直角三角形底边,先求出CD,然后得到小等腰直角三角形的底和高,再利用大直角三角形的面积减去小直角三角形面积即可
【详解】如图:过顶点A作AB⊥大直角三角形底边
由题意: SKIPIF 1 < 0
∴ SKIPIF 1 < 0
= SKIPIF 1 < 0 cm
∴小等腰直角三角形的直角边为 SKIPIF 1 < 0 cm
∴大等腰直角三角形面积为10×10÷2=50cm2
小等腰直角三角形面积为 SKIPIF 1 < 0 =36-16 SKIPIF 1 < 0 cm2
∴ SKIPIF 1 < 0
【点睛】本题主要考查阴影部分面积的计算,涉及到直角三角形的基本性质,本题关键在于做出正确的辅助线进行计算
1.已知:如图, SKIPIF 1 < 0 的圆心为 SKIPIF 1 < 0 ,半径为2, SKIPIF 1 < 0 切 SKIPIF 1 < 0 于 SKIPIF 1 < 0 点,则阴影部分的面积为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
【答案】A
【分析】此题考查了切线的性质定理,扇形面积计算公式,锐角三角函数求角的度数,连接 SKIPIF 1 < 0 ,得到 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,根据 SKIPIF 1 < 0 求解.
【详解】连接 SKIPIF 1 < 0 ,
∵ SKIPIF 1 < 0 切 SKIPIF 1 < 0 于 SKIPIF 1 < 0 点,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∵ SKIPIF 1 < 0 的圆心为 SKIPIF 1 < 0 ,半径为2,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 SKIPIF 1 < 0 SKIPIF 1 < 0 ,
故选:A.
2.如图所示,将一副三角尺叠放在一起,若 SKIPIF 1 < 0 ,则阴影部分的面积是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
【答案】D
【分析】本题考查等腰直角三角形的判定与性质,由于 SKIPIF 1 < 0 ,那么 SKIPIF 1 < 0 是等腰直角三角形,可根据三角形面积的计算方法求出阴影部分的面积.
【详解】解:由题意可知 SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 .
故 SKIPIF 1 < 0 .
故选:D.
3.如图,在 SKIPIF 1 < 0 中, SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,以点C为圆心作半圆,其直径 SKIPIF 1 < 0 .将 SKIPIF 1 < 0 沿 SKIPIF 1 < 0 方向平移5个单位长度,得到 SKIPIF 1 < 0 ,则图中阴影部分的面积为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
【答案】A
【分析】本题考查了解直角三角形,求扇形面积,平移的性质;设 SKIPIF 1 < 0 交半圆 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ,连接 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ,根据平移得出 SKIPIF 1 < 0 ,进而得出 SKIPIF 1 < 0 ,根据阴影部分面积等于 SKIPIF 1 < 0 即可求解.
【详解】解:如图所示,设 SKIPIF 1 < 0 交半圆 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ,连接 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0
∵将 SKIPIF 1 < 0 沿 SKIPIF 1 < 0 方向平移5个单位长度,得到 SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0
∴阴影部分面积为 SKIPIF 1 < 0
故选:A.
4.已知 SKIPIF 1 < 0 为 SKIPIF 1 < 0 的直径,C为 SKIPIF 1 < 0 上一点,将 SKIPIF 1 < 0 绕着点A顺时针旋转一定的角度后得到 SKIPIF 1 < 0 ,交 SKIPIF 1 < 0 于E点,若点D在 SKIPIF 1 < 0 上, SKIPIF 1 < 0 ,则阴影部分的面积为( )
A.8B.16C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
【答案】A
【分析】连接 SKIPIF 1 < 0 、 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,连接 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于 SKIPIF 1 < 0 ,由旋转的性质得 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 与 SKIPIF 1 < 0 是等圆,由圆的基本性质得 SKIPIF 1 < 0 ,可得 SKIPIF 1 < 0 , 由三角形相似判定方法得 SKIPIF 1 < 0 ,由三角形相似的性质得 SKIPIF 1 < 0 求出 SKIPIF 1 < 0 ,由勾股定理 SKIPIF 1 < 0 求出 SKIPIF 1 < 0 ,再由三角形面积公式即可求解.
【详解】解:如图,连接 SKIPIF 1 < 0 、 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,连接 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于 SKIPIF 1 < 0 ,
SKIPIF 1 < 0 SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 SKIPIF 1 < 0 ,
由旋转得: SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 与 SKIPIF 1 < 0 是等圆,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 SKIPIF 1 < 0 ,
SKIPIF 1 < 0 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
SKIPIF 1 < 0 是直径,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0 ;
故选:A.
【点睛】本题考查了旋转的性质,圆的基本性质,线段垂直平分线的判定定理,三角形相似的判定及性质,勾股定理等;掌握性质,能作出恰当的辅助线,证出 SKIPIF 1 < 0 , SKIPIF 1 < 0 是解题的关键.
5.如图,直角三角板 SKIPIF 1 < 0 的锐角顶点A落在 SKIPIF 1 < 0 上,其中 SKIPIF 1 < 0 ,边 SKIPIF 1 < 0 、 SKIPIF 1 < 0 分别与 SKIPIF 1 < 0 交于D、E两点,连接 SKIPIF 1 < 0 ,若 SKIPIF 1 < 0 的半径为4,则图中阴影部分的面积为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
【答案】A
【分析】本题考查圆周角定理,扇形的面积,先根据圆周角定理得到 SKIPIF 1 < 0 的度数,然后利用 SKIPIF 1 < 0 计算是解题的关键.
【详解】解:连接 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∵ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
故选A.
6.如图,在 SKIPIF 1 < 0 中, SKIPIF 1 < 0 , SKIPIF 1 < 0 ,以 SKIPIF 1 < 0 为直径的 SKIPIF 1 < 0 与 SKIPIF 1 < 0 边相切于点E,与 SKIPIF 1 < 0 边相交于点F,连接 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则图中阴影部分的面积为 .
【答案】 SKIPIF 1 < 0
【分析】该题主要考查了圆的切线的性质,圆周角定理,平行四边形的性质,扇形面积计算,解答的关键是掌握以上知识点.
根据 SKIPIF 1 < 0 是平行四边形和圆周角定理,证明 SKIPIF 1 < 0 ,再根据 SKIPIF 1 < 0 与 SKIPIF 1 < 0 相切得出 SKIPIF 1 < 0 ,从而算出 SKIPIF 1 < 0 ,再根据扇形面积计算公式计算即可.
【详解】∵ SKIPIF 1 < 0 是平行四边形,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 .
∵ SKIPIF 1 < 0 与 SKIPIF 1 < 0 相切,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 .
∵ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
所以阴影部分的面积为 SKIPIF 1 < 0 .
故答案为: SKIPIF 1 < 0 .
7.黄金分割比是让无数科学家、数学家、艺术家为之着迷的数字.黄金矩形的长宽之比为黄金分割比,即矩形的短边为长边的 SKIPIF 1 < 0 倍.黄金分割比能够给画面带来美感,令人愉悦,在很多艺术品以及大自然中都能找到它.比如蜗牛壳的螺旋中就隐藏了黄金分割比.如图,用黄金矩形 SKIPIF 1 < 0 框住整个蜗牛壳,之后作正方形 SKIPIF 1 < 0 ,得到黄金矩形 SKIPIF 1 < 0 ,再作正方形 SKIPIF 1 < 0 ,得到黄金矩形 SKIPIF 1 < 0 ……,这样作下去,我们以每个小正方形边长为半径画弧线,然后连接起来,就是黄金螺旋.已知 SKIPIF 1 < 0 ,则阴影部分的面积为 .
【答案】 SKIPIF 1 < 0
【分析】本题主要考查了求不规则图形面积,矩形的性质,正方形的性质,理解黄金矩形的定义是解题的关键.根据黄金矩形的定义可得 SKIPIF 1 < 0 的长,从而得到 SKIPIF 1 < 0 的长,再由阴影部分的面积 SKIPIF 1 < 0 ,即可求解.
【详解】解:∵四边形 SKIPIF 1 < 0 是黄金矩形, SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∵四边形 SKIPIF 1 < 0 是正方形,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∴阴影部分的面积 SKIPIF 1 < 0 .
故答案为: SKIPIF 1 < 0 .
8.如图,已知正 SKIPIF 1 < 0 的边长为 SKIPIF 1 < 0 ,把正 SKIPIF 1 < 0 绕着它的中心O旋转,当旋转至正 SKIPIF 1 < 0 的位置,其中 SKIPIF 1 < 0 ,则图中阴影部分的面积为 .
【答案】 SKIPIF 1 < 0
【分析】根据圆的旋转不变性,易知图中的6个小直角三角形都全等,则图中阴影部分的面积为圆的面积减去一个正三角形的面积,再减去3个小直角三角形的面积即可求出阴影部分的面积.
【详解】解:根据圆的旋转不变性,易知图中的6个小直角三角形都全等,则图中阴影部分的面积为圆的面积减去一个正三角形的面积,再减去3个小直角三角形的面积.
如图1,连接 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ,延长 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点P,
则 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 分别平分等边三角形的顶角,且 SKIPIF 1 < 0 ,
SKIPIF 1 < 0 , SKIPIF 1 < 0 为等边三角形,
SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
设 SKIPIF 1 < 0 、 SKIPIF 1 < 0 交于点Q,连接 SKIPIF 1 < 0 ,延长 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点N,
则 SKIPIF 1 < 0 ,
∵ SKIPIF 1 < 0 ,
∴四边形 SKIPIF 1 < 0 为矩形,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∵ SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 .
如图2,在 SKIPIF 1 < 0 中,过点Q作 SKIPIF 1 < 0 ,交 SKIPIF 1 < 0 于点M, SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
设 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
解得: SKIPIF 1 < 0 ,
则 SKIPIF 1 < 0 ,
在 SKIPIF 1 < 0 中, SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0 .
故答案为: SKIPIF 1 < 0 .
【点睛】本题主要考查了圆与多边形,等边三角形的性质,旋转的性质.解直角三角形,三角形全等的判定和性质,矩形的判定和性质,解题的关键是作出辅助线,熟练掌握相关的判定和性质.
9.如图,平行于地面的三角形纸片上方有一灯泡(看作一个点O),灯泡发出的光线照射 SKIPIF 1 < 0 后,在地面上形成阴影 SKIPIF 1 < 0 .已知灯泡距离地面3m,灯泡距离纸片1m,则阴影 SKIPIF 1 < 0 与纸片 SKIPIF 1 < 0 的面积比为 .
【答案】 SKIPIF 1 < 0 /9
【分析】本题考查了相似三角形的应用,熟练掌握相似三角形的判定与性质是解题的关键.
根据题意可得: SKIPIF 1 < 0 ,然后利用相似三角形的性质可得答案.
【详解】解:由题意得: SKIPIF 1 < 0 ,
SKIPIF 1 < 0 SKIPIF 1 < 0 ,
故答案为: SKIPIF 1 < 0 .
10.如图,点 SKIPIF 1 < 0 是圆形纸片的圆心,将这个圆形纸片按下列顺序折叠,使弧 SKIPIF 1 < 0 和弧 SKIPIF 1 < 0 都经过圆心 SKIPIF 1 < 0 ,已知 SKIPIF 1 < 0 的半径为 SKIPIF 1 < 0 ,则阴影部分的面积是 .
【答案】 SKIPIF 1 < 0
【分析】综合运用折叠性质、圆的基本性质、勾股定理、垂径定理、三角函数特殊值判断角度推出所求阴影部分面积为圆心角 SKIPIF 1 < 0 的扇形面积,再根据扇形面积公式即可求解.
【详解】解:连接 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ,作 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ,
依题得, SKIPIF 1 < 0 ,
由折叠性质得, SKIPIF 1 < 0
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 中, SKIPIF 1 < 0 ,
又 SKIPIF 1 < 0 是半径,
SKIPIF 1 < 0 , SKIPIF 1 < 0
SKIPIF 1 < 0 平分弧 SKIPIF 1 < 0 与弦 SKIPIF 1 < 0 组成的图形,
SKIPIF 1 < 0 , SKIPIF 1 < 0
SKIPIF 1 < 0 ,
即 SKIPIF 1 < 0 ,
又 SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 弧 SKIPIF 1 < 0 与弦 SKIPIF 1 < 0 组成图形的面积 SKIPIF 1 < 0 弧 SKIPIF 1 < 0 与弦 SKIPIF 1 < 0 组成图形的面积;
同理可得, SKIPIF 1 < 0 ,弧 SKIPIF 1 < 0 与弦 SKIPIF 1 < 0 组成图形的面积=弧 SKIPIF 1 < 0 与弦 SKIPIF 1 < 0 组成图形的面积,
SKIPIF 1 < 0 ,
即所求阴影部分面积为圆心角 SKIPIF 1 < 0 的扇形面积,
SKIPIF 1 < 0 .
故答案为: SKIPIF 1 < 0 .
【点睛】本题考查的知识点是折叠性质、圆的基本性质、垂径定理、勾股定理、三角函数特殊值判断角度、扇形面积的计算,解题关键是将两部分阴影部分面积转化为扇形面积.
2024年中考数学压轴题型(江苏专用)专题03 代数与几何最值题(选择填空压轴题)(含解析): 这是一份2024年中考数学压轴题型(江苏专用)专题03 代数与几何最值题(选择填空压轴题)(含解析),共15页。试卷主要包含了 代数方法, 几何方法, 综合方法等内容,欢迎下载使用。
2024年中考数学压轴题型(江苏专用)专题02 函数与几何综合题(填空压轴题)(含解析): 这是一份2024年中考数学压轴题型(江苏专用)专题02 函数与几何综合题(填空压轴题)(含解析),共21页。试卷主要包含了 理解题意, 建立函数关系,利用函数性质, 几何分析, 代数运算, 验证答案, 总结与反思等内容,欢迎下载使用。
2024年中考数学压轴题型(江苏专用)专题01 几何与函数图象结合(选择压轴题)(含解析): 这是一份2024年中考数学压轴题型(江苏专用)专题01 几何与函数图象结合(选择压轴题)(含解析),共22页。试卷主要包含了 理解题意,建立联系, 利用几何性质, 代数运算, 验证答案, 总结与反思等内容,欢迎下载使用。












