数学苏科版2.5 直线与圆的位置关系教课内容ppt课件

这是一份数学苏科版2.5 直线与圆的位置关系教课内容ppt课件，共27页。PPT课件主要包含了教学目标，情境引入，知识精讲，三角形的内切圆与内心，确定圆的条件，三角形的内心，三角形的外心VS外心，外接圆，内切圆，垂直平分线等内容，欢迎下载使用。
理解三角形的内切圆与内心的概念，与三角形的外接圆与外心的概念进行区分
掌握三角形内切圆与内心的有关性质与角度结论
掌握三角形内切圆半径的计算公式
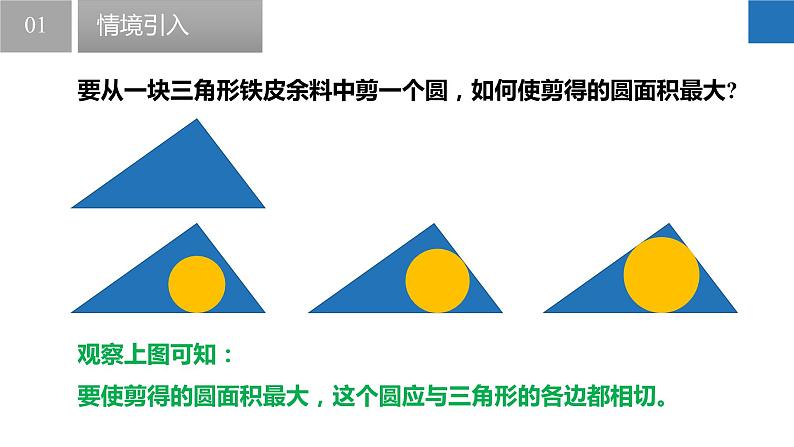
要从一块三角形铁皮余料中剪一个圆，如何使剪得的圆面积最大?
观察上图可知：要使剪得的圆面积最大，这个圆应与三角形的各边都相切。
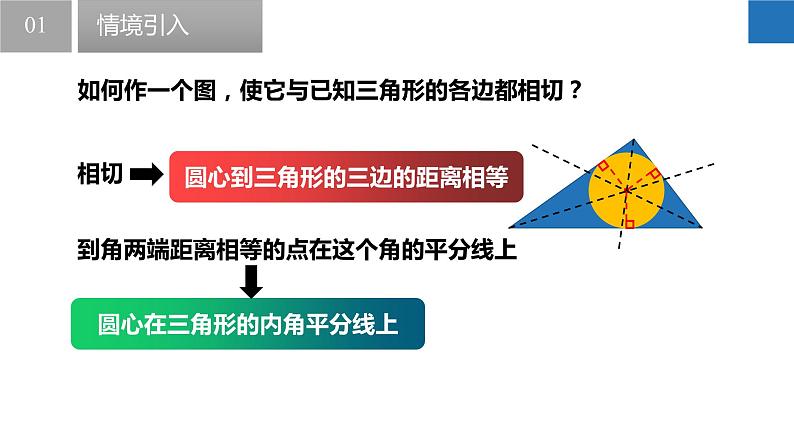
如何作一个图，使它与已知三角形的各边都相切？
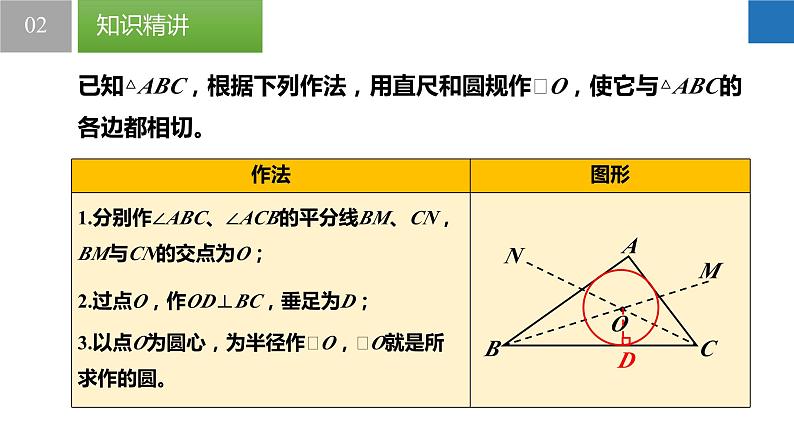
已知△ABC，根据下列作法，用直尺和圆规作⨀O，使它与△ABC的各边都相切。
1.分别作∠ABC、∠ACB的平分线BM、CN，BM与CN的交点为O；
2.过点O，作OD⊥BC，垂足为D；
3.以点O为圆心，为半径作⨀O，⨀O就是所求作的圆。
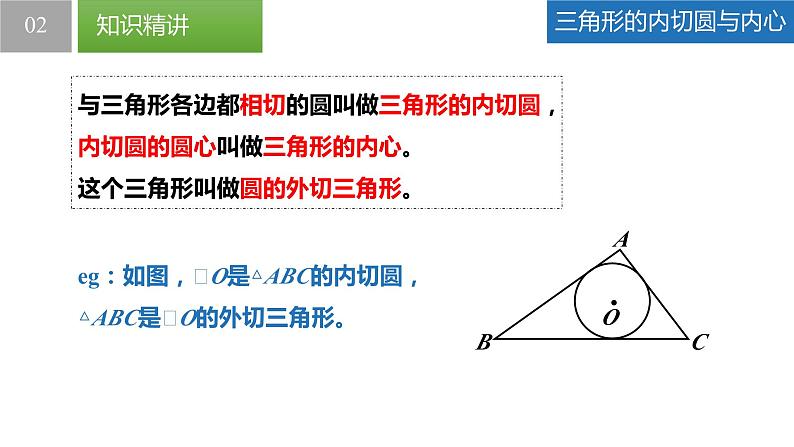
eg：如图，⨀O是△ABC的内切圆，△ABC是⨀O的外切三角形。
与三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心。这个三角形叫做圆的外切三角形。
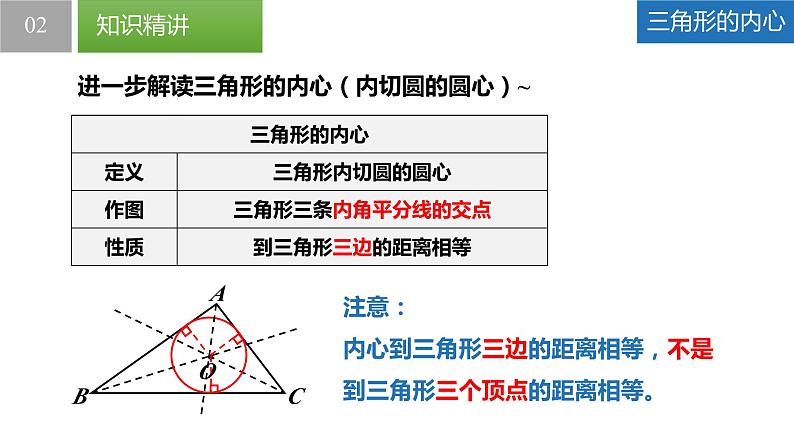
进一步解读三角形的内心（内切圆的圆心）~
注意：内心到三角形三边的距离相等，不是到三角形三个顶点的距离相等。
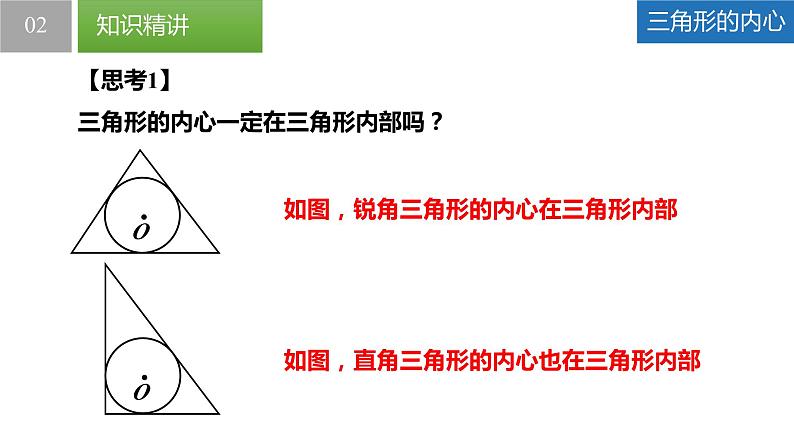
【思考1】三角形的内心一定在三角形内部吗？
如图，锐角三角形的内心在三角形内部
如图，直角三角形的内心也在三角形内部
如图，钝角三角形的内心还在三角形内部
三角形的内心一定在三角形内部。
三角形的内切圆与圆的外切三角形
【思考2-1】一个三角形的内切圆有几个？
∵三角形内切圆的圆心是三角形三条内角平分线的交点，有且只有一个，∴一个三角形的内切圆有且只有1个。
【思考2-2】一个圆的外切三角形有几个？
如图，一个圆的外切三角形有无数个。
一个三角形的内切圆有且只有1个，一个圆的外切三角形有无数个。
例1、（1）如图，O是△ABC的内心，∠BOC=100°，则∠A=_______；
【分析】∵O是△ABC的内心，∴OB、OC是∠ABC、∠ACB的角平分线，∴∠ABC=2∠OBC，∠ACB=2∠OCB，又∵∠BOC=100°，∴∠OBC+∠OCB=80°，∴∠ABC+∠ACB=160°，∴∠A=20°。
例1、（2）如图，O是△ABC的内心，探究∠BOC与∠A之间的数量关系。
例2、如图，点I和O是△ABC的内心和外心，若∠AIB=125°，则∠AOB=_______。
三角形内切圆的半径问题
例1、（1）若三角形的三边长分别为3、4、5，求三角形内切圆的半径。
解：（1）法一：如图，设AC=3，AB=4，BC=5，⨀O与△ABC分别切于点D、E、F，OD=OE=OF=r，
法二：∵∠AFO=∠AEO=90°=∠BAC，且OE=OF，∴四边形AFOE是正方形，AF=AE=r，∴BF=4-r，CE=3-r，又∵△BOD≌BOF△(HL)，△COD≌△COE(HL)，∴BD=BF=4-r，CD=CE=3-r，∴BC=BD+CD=4-r+3-r=7-2r=5，解得：r=1。
例2、若三角形的面积为S，周长为C，求三角形内切圆的半径。
解：如图，设⨀O与△ABC分别切于点D、E、F，OD=OE=OF=r，
例3、若直角三角形的的三边长分别为a、b、c，求三角形内切圆的半径。
解：如图，设⨀O与△ABC分别切于点D、E、F，OD=OE=OF=r，∠BAC=90°,
∵∠AFO=∠AEO=90°=∠BAC，且OE=OF，∴四边形AFOE是正方形，AF=AE=r，∴BF=c-r，CE=b-r，
练1、若三角形的三边长分别为12、12、10，求三角形内切圆的半径。
解：如图，设AB=AC=12，BC=10，过点A作AD⊥BC交于点D，
练2、若三角形的三边长分别为5、12、13，求三角形内切圆的半径。