苏科版九年级上册2.6 正多边形与圆说课ppt课件

这是一份苏科版九年级上册2.6 正多边形与圆说课ppt课件，共31页。PPT课件主要包含了教学目标，情境引入，知识精讲，正多边形，正多边形与圆，正多边形有关的概念，正多边形有关的计算，正多边形的性质，典例精析，正多边形的作法等内容，欢迎下载使用。
认识正多边形，理解圆的内接正n边形、正n边形的外接圆的概念
理解正多边形的有关概念，掌握正多边形的有关计算
能借助尺规作出一些特殊的正多边形
我们已经学习过等边三角形（正三角形）、正方形（正四边形），正三角形、正四边形的各边相等，各角也相等。
生活中，各边相等、各角也相等的多边形的形象处处可见~
正多边形：各边相等、各角也相等的多边形叫做正多边形。
【思考1】已知：三边相等的三角形是正三角形，三角相等的三角形也是正三角形，问：各边相等的多边形是正多边形吗？或各角相等的多边形是正多边形吗？
各角相等的多边形不一定是正多边形
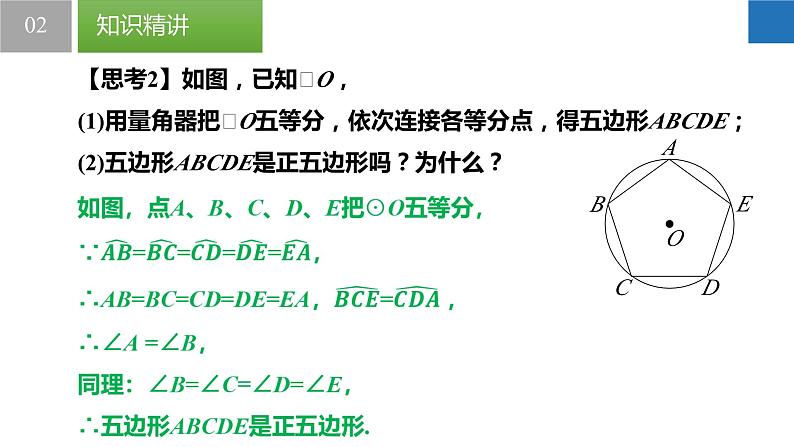
【思考2】如图，已知⨀O，(1)用量角器把⨀O五等分，依次连接各等分点，得五边形ABCDE；(2)五边形ABCDE是正五边形吗？为什么？
【思考3】如图，点A、B、C、D、E、F把⨀O六等分.(1)在一张透明纸上画与图中形状、大小相同的图形，并把它们叠合在一起；
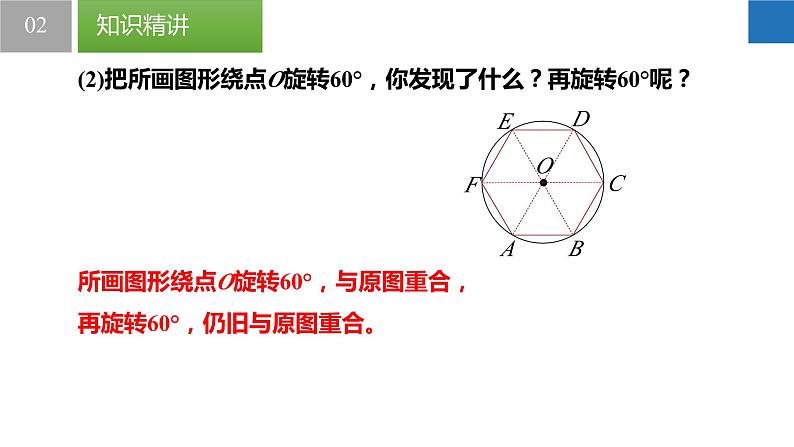
(2)把所画图形绕点O旋转60°，你发现了什么？再旋转60°呢？
所画图形绕点O旋转60°，与原图重合，再旋转60°，仍旧与原图重合。
(3)你能用图形运动的方法证实六边形ABCDEF是正六边形吗?
∵所画图形绕点O每旋转60°，仍旧与原图重合，∴AB=BC=CD=DE=EF=FA，∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA，∴六边形ABCDEF是正六边形。
一般地，只要用量角器把一个圆n(n≥3)等分，依次连接各等分点就能得到这个圆的内接正n边形，这个圆是这个正n边形的外接圆。
1、正多边形的外接圆的圆心叫做正多边形的中心；2、外接圆的半径叫做正多边形的半径；3、正多边形每一边所对的圆心角叫做正多边形的中心角；4、中心到正多边形的一边的距离叫做正多边形的边心距。
【思考4】分别求半径为R的圆的内接正三角形、正方形、正六边形的边长、中心角、边心距、周长和面积。
【思考5】图中的正多边形，哪些是轴对称图形？哪些是中心对称图形？如果是轴对称图形，画出它的对称轴；如果是中心对称图形，找出它的对称中心。
轴对称图形：正三角形、正方形、正五边形、正六边形；中心对称图形：正方形、正六边形。
【思考6】连接图中正多边形的半径和边心距，你发现了什么？
正三角形分成6个全等的直角三角形；正方形分成8个全等的直角三角形；正五边形分成10个全等的直角三角形；正六边形分成12个全等的直角三角形。
1、轴对称性：正多边形都是轴对称图形，一个正n边形共有n条对称轴，每条对称轴都经过正n边形的中心。2、中心对称性：一个正多边形，如果有偶数条边，那么它是中心对称图形，对称中心就是这个正多边形的中心。3、正多边形的半径和边心距把正n边形分成2n个全等的直角三角形。
例1、如图，A、B、C、D为一个正多边形的顶点，O为正多边形的中心．若∠ADB=18°，则这个正多边形的边数为________。
例2、已知⨀O的半径为6，则它的内接正三角形边心距为________。
例3、已知一个正多边形的中心角为45°，边长为5，那么这个正多边形的周长等于________。
【分析】∵该正多边形的中心角为45°，∴正多边形的边数为：360°÷45°=8，∴该正多边形的周长为：5×8=40．
例4、已知圆内接正六边形的边长是1，则该圆的内接正三角形的面积为________。
用直尺和圆规可以作出一些特殊的正多边形~
【思考1】如何作正八边形？
【思考2】如何作正三角形？
【思考3】如何作正十二边形？
正多边形：各边相等、各角也相等的多边形叫做正多边形。一般地，只要用量角器把一个圆n(n≥3)等分，依次连接各等分点就能得到这个圆的内接正n边形，这个圆是这个正n边形的外接圆。
正多边形有关的概念：1、正多边形的外接圆的圆心叫做正多边形的中心；2、外接圆的半径叫做正多边形的半径；3、正多边形每一边所对的圆心角叫做正多边形的中心角；4、中心到正多边形的一边的距离叫做正多边形的边心距。