第2章 对称图形——圆 单元测试-2023-2024学年九年级数学上册（苏科版）

这是一份第2章 对称图形——圆 单元测试-2023-2024学年九年级数学上册（苏科版），文件包含第2章对称图形圆原卷版单元docx、第2章对称图形圆解析版单元docx等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。

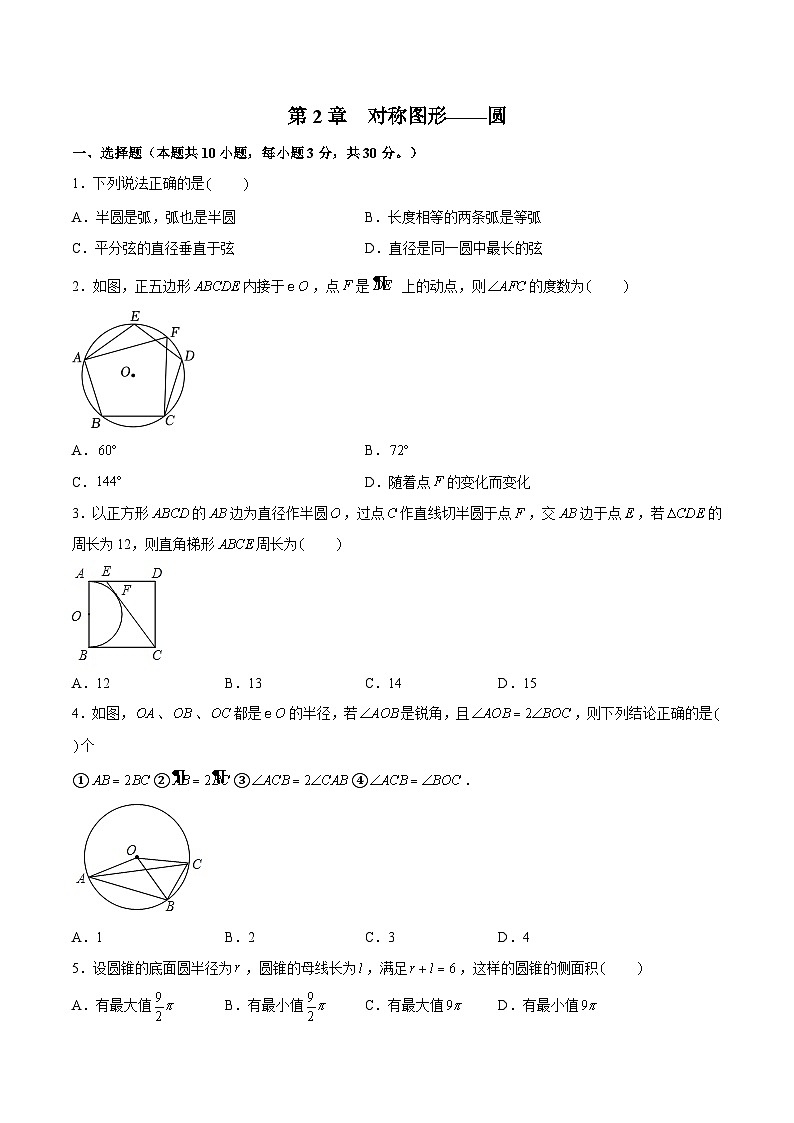
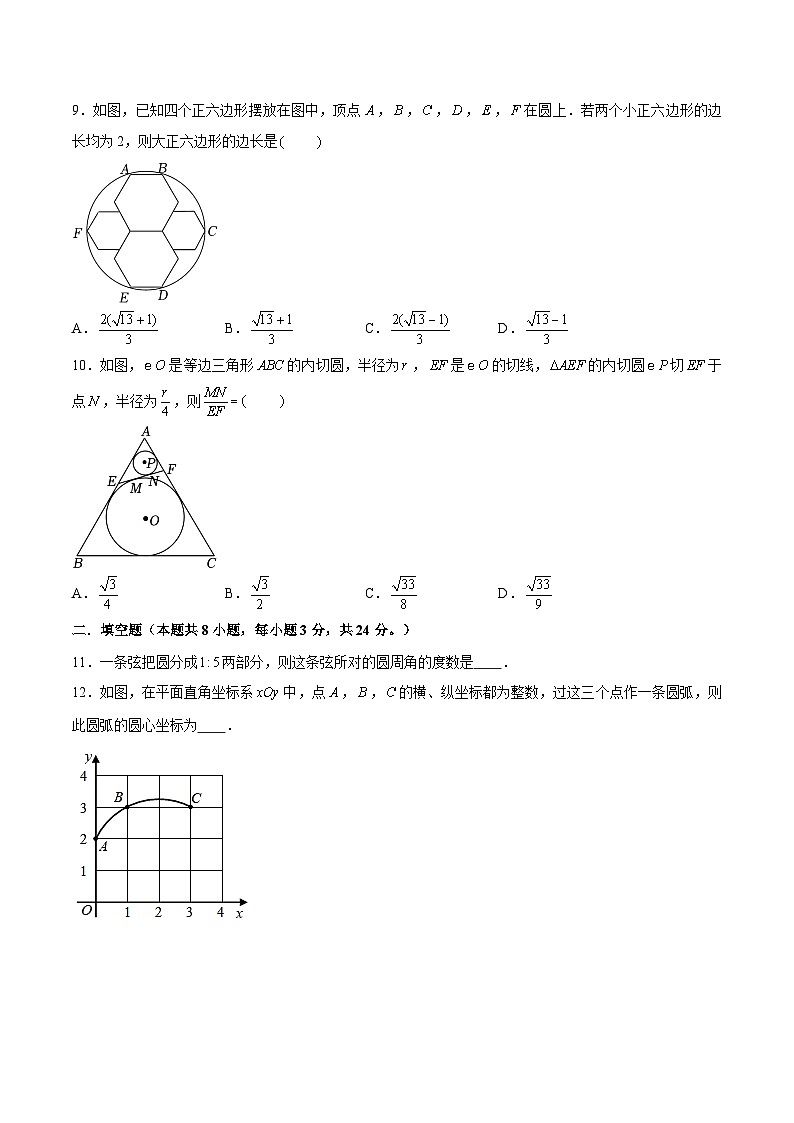
班级 姓名 学号 分数 第2章 对称图形——圆（时间：120分钟，满分：130分）一、选择题（本题共10小题，每小题3分，共30分。）1．下列说法正确的是　　A．半圆是弧，弧也是半圆 B．长度相等的两条弧是等弧 C．平分弦的直径垂直于弦 D．直径是同一圆中最长的弦【详解】解：半圆是弧，弧不一定是半圆，故不合题意；同圆或等圆中，长度相等的两条弧是等弧，故不合题意；平分弦（不是直径）的直径垂直于弦，不合题意；直径是同一圆中最长的弦，故符合题意．故本题选：．2．如图，正五边形内接于，点是 上的动点，则的度数为　　A． B． C． D．随着点的变化而变化【详解】解：如图，连接、、，五边形是的内接正五边形，，，．故本题选：．3．以正方形的边为直径作半圆，过点作直线切半圆于点，交边于点，若的周长为12，则直角梯形周长为　　A．12 B．13 C．14 D．15【详解】解：设的长为，正方形的边长为，与半圆相切于点，，，，，，正方形的边长为4，在中，，即，解得：，，直角梯形周长为14．故本题选：．4．如图，、、都是的半径，若是锐角，且，则下列结论正确的是　　个①②③④．A．1 B．2 C．3 D．4【详解】解：如图，取的中点，连接，，，，故②正确；，，，．故①错误；，，，，，故③④正确．故本题选：．5．设圆锥的底面圆半径为，圆锥的母线长为，满足，这样的圆锥的侧面积　　A．有最大值 B．有最小值 C．有最大值 D．有最小值【详解】解：由题意知：，，当时，此时最大，为．故本题选：．6．如图，在半圆中，，将半圆沿弦所在的直线折叠，若恰好过圆心，则的长是　　A． B． C． D．4 【详解】解：如图，过点作于，交半圆于点，连接，半圆沿所在的直线折叠，圆弧恰好过圆心，，，，，即，为直径，，．故本题选：．7．我们知道：过圆外一点所画的圆的两条切线长相等．问题解决如图，现有一块边长为的正方形空地，在边取一点，以长为直径，在这个正方形的空地内建一个半圆形儿童游乐场，过点划出一条与这个半圆相切的分割线，正方形位于分割线右下方的部分作为娱乐区，娱乐区的最大面积等于　　A． B． C． D．【详解】解：如图，当半圆面积最大，即与重合时，娱乐区的面积最大，与半圆相切于，交于，四边形是正方形，，，，分别是半圆的切线，，，设，则，，，在中，，，，，娱乐区的最大面积梯形的面积．故本题选：．8．如图，、是的两条弦，，，垂足为点，点为的中点，延长交于点，若，的面积为15，，则为　　A． B． C．10 D．9【详解】解：，点是的中点，，，，，，即，设，则，，，即，或，，，．故本题选：．9．如图，已知四个正六边形摆放在图中，顶点，，，，，在圆上．若两个小正六边形的边长均为2，则大正六边形的边长是　　A． B． C． D．【详解】解：如图，由正六边形的性质可知：在小正六边形中，，则，在大正六边形中，，设，则，，，由于，，解得：（舍去）或，即．故本题选：．10．如图，是等边三角形的内切圆，半径为，是的切线，的内切圆切于点，半径为，则　　A． B． C． D．【详解】解：如图，设与、的切点分别是、，与、的切点分别是、，连接、、、、、，过作垂直于，垂足为，则，，，，，，，，，，是的角平分线，，，，在上，中，，①，中，，②，②①得：，，，四边形是矩形，，，在中，，，，，．故本题选：．二．填空题（本题共8小题，每小题3分，共24分。）11．一条弦把圆分成两部分，则这条弦所对的圆周角的度数是　　．【详解】解：如图，连接、，一条弦把圆分成两部分，弧的度数是，弧的度数是，，，．故本题答案为：或．12．如图，在平面直角坐标系中，点，，的横、纵坐标都为整数，过这三个点作一条圆弧，则此圆弧的圆心坐标为　　．【详解】解：从图形可知：点的坐标是，点的坐标是，点的坐标是，如图，连接，作线段和线段的垂直平分线、，两线交于，则是圆弧的圆心，点的坐标是．故本题答案为：．13．如图，已知在直角三角形ABC中，∠ACB＝90°，AB＝5，AC＝3，BC＝4，将三角形ABC绕顶点A顺时针旋转45°（即∠BAB′＝45°）后得到△AB′C′，那么图中阴影部分的面积与周长的比值为　　．（精确到0.01）【详解】解：由旋转的性质得：AC′＝AC＝3，B′C′＝BC＝4，AB′＝AB＝5，△AB′C′的面积等于△ABC的面积，∵∠BAB′＝45°，∴阴影部分的面积为45×π×52360+S△AB′C′−S△ABC=25π8，阴影部分的周长为4+4+3+3+45×π×5180=56+5π4，则图中阴影部分的面积与周长的比值为25π8：56+5π4≈0.55．故本题答案为：0.55．14．已知的三边长分别为2、2和．若将绕其任意一边所在的直线旋转一周，则所得几何体的表面积是　　．【详解】解：①当绕边长为2的边所在的直线旋转一周时，所得几何体为圆锥，表面积是；②当绕边长为的边所在的直线旋转一周时，所得几何体的表面积是；综上，所得几何体的表面积是或．故本题答案为：或．15．如图，在中，弦，点在上移动，连接，过点作，交于点，则长的最大值为　　．【详解】解：，，，当的值最小时，的值最大，时，最小，此时、两点重合，，即的最大值为2．故本题答案为：2．16．如图，中，，，，是边上的高，，分别是，的内切圆，则与的面积比为　　．【详解】解：在中，，，，，，，在中，由勾股定理得：，，设的半径为，的半径为，则，即，，同理：，与的面积比为．故本题答案为：．17．如图，在中，，，，平分，点为线段上一动点．以点为圆心、以1为半径作圆，当与的边相切时，的长为　　．【详解】解：，，，平分，，，，，①若与相切于点，如图，连接，则，平分，过点作，，此时与相切，，，；②若与相切于点，如图，连接，则，，，，，，；综上，当与的边相切时，长为2或．故本题答案为：2或．18．如图，以为圆心，半径为2的圆与轴交于、两点，与轴交于，两点，点为上一动点，于，则弦的长度为　　；当点在的运动过程中，线段的长度的最小值为　　．【详解】解：如图，作于，连接，，，在中，，，，，，；，，，，，，，，点在以为直径的上，当点在的延长线上时，的长最小，最小值．故本题答案为：，．三．解答题（本题共10小题，共66分。）19．（6分）如图，是的直径，是的中点，于点，交于点．（1）求证：；（2）若，，求的半径及的长．【详解】（1）证明：是的直径，，．，，，．又是的中点，，，，；（2）解：，，，，的半径为5，，．20．（6分）某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，如图是水平放置的破裂管道有水部分的截面．（1）若这个输水管道有水部分的水面宽，水面最深地方的高度为，求这个圆形截面的半径；（2）在（1）的条件下，小明把一只宽的方形小木船放在修好后的圆柱形水管里，已知船高出水面，问此小船能顺利通过这个管道吗？【详解】解：（1）如图，过作于，交弧于，连接，，，由题意可知：，设半径为，则，在中，由勾股定理得：，，解得：，即这个圆形截面的半径为；（2）小船能顺利通过这个管道，理由如下：如图，连接，设．，，在中，，，，小船能顺利通过这个管道．21．（8分）如图，AB为⊙O的直径，过圆上一点D作⊙O的切线CD交BA的延长线于点C，过点O作OE∥AD，OE交CD于点E，连接BE．（1）求证：直线BE与⊙O相切；（2）若CA＝2，CD＝4，求DE的长．【详解】（1）证明：连接OD，∵CD与⊙O相切于点D，∴∠ODE＝90°，∵AD//OE，∴∠ADO＝∠DOE，∠DAO＝∠EOB，∵OD＝OA，∴∠ADO＝∠DAO，∴∠DOE＝∠EOB，∵OD＝OB，OE＝OE，∴△DOE≌△BOE（SAS），∴∠OBE＝∠ODE＝90°，∵OB是⊙O的半径，∴直线BE与⊙O相切；（2）解：设⊙O的半径为r，在Rt△ODC中，OD2+DC2＝OC2，∴r2+42＝(r+2)2，∴r＝3，∴AB＝2r＝6，∴BC＝AC+AB＝2+6＝8，由（1）得：△DOE≅△BOE，∴DE＝BE，在Rt△BCE中，BC2+BE2＝CE2，∴82+BE2＝(4+DE)2，∴64+DE2＝(4+DE)2，∴DE＝6，∴DE的长为6．22．（8分）如图1是小明制作的一副弓箭，点，分别是弓臂与弓弦的中点，弓弦，沿方向拉弓的过程中，假设弓臂始终保持圆弧形，弓弦长度不变．如图2，当弓箭从自然状态的点拉到点时，有，．（1）图2中，求弓臂两端是多少厘米？（2）如图3，将弓箭继续拉到点，使弓臂为半圆，求是多少厘米？【详解】解：（1）如图，连接，交于点，，点是弓臂的中点，点是弧所在圆的圆心，，，，在△中，，；（2）如图，连接交于点，由（1）可得：弧的长，设所在圆的半径为，弧的长，解得：，，，，在△中，根据勾股定理可得：，．23．（8分）【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积？【初步尝试】如图1，已知扇形，请你用圆规和无刻度的直尺过圆心作一条直线，使扇形的面积被这条直线平分；【问题联想】如图2，已知线段，请你用圆规和无刻度的直尺作一个以为斜边的等腰直角三角形；【问题再解】如图3，已知扇形，请你用圆规和无刻度的直尺作一条以点为圆心的圆弧，使扇形的面积被这条圆弧平分．（友情提醒：以上作图均不写作法，但需保留作图痕迹）【详解】解：【初步尝试】如图1，直线即为所求；【问题联想】如图2，三角形即为所求；【问题再解】如图3中，即为所求．24．（10分）已知，在半圆中，直径，点，在半圆上运动，弦．（1）如图1，当时，求证：；（2）如图2，若，求图中阴影部分（弦、直径、弧围成的图形）的面积；（3）如图3，取的中点，点从点开始运动到点与点重合时结束，在整个运动过程中：点到的距离的最小值是　　．【详解】（1）证明：，，，，，，，又，；（2）解：如图2，过作于，连接，半圆中，直径，，，，，，，；（3）如图3，连接，，是的中点，，，，点在以为圆心，为半径的圆弧上运动，过作，垂足为，，，点到的距离的最小值是．故本题答案为：．25．（10分）在一次数学兴趣小组活动中，小亮利用同弧所对的圆周角及圆心角的性质探索了一些问题，下面请你和小亮一起进入探索之旅．【问题探索】（1）如图1，点、、、在上，点在外，且，则　　，　　，　　．（填“”、“ ”或“”）．【操作实践】（2）如图2，已知线段和直线，用直尺和圆规在直线上作出所有点，使．（要求：用直尺与圆规作出点，保留作图痕迹，不写作法．）【迁移应用】（3）请运用探索所得的学习经验，解决问题：如图3，已知的半径为2，，点为优弧上一动点，交的延长线于点．①求的度数；②面积的最大值．【详解】解：（1）如图1，设交于点，连接，点、、、、在上，且，，，，，故本题答案为：45，90，；（2）作法：1．分别以点、为圆心，长为半径作弧，两弧在上方交于点，2．连接，以点为圆心，长为半径作圆，交直线于点和点，点、点就是所求得点，理由如下：如图，连接、、、、，根据作图得：，点在上，，，点、点就是所求得点；（3）①如图3，连接、，则，，，是直角三角形，且，，，，，的度数是；②如图4，作的外接圆，连接、，则，，作于点，交于点，使点与点在的同侧，连接、，，，，，，作交的延长线于点，连接、，则，为定值，当的值最大时，则的面积最大，，，，当点与点重合时，，此时的值最大，，的面积的最大值为．26．（10分）【概念认识】在同一个圆中两条互相垂直且相等的弦定义为“等垂弦”，两条弦所在直线的交点为等垂弦的分割点．如图①，、是的弦，，，垂足为，则、是等垂弦，为等垂弦、的分割点．【数学理解】（1）如图②，是的弦，作、，分别交于点、，连接．求证：、是的等垂弦．（2）在中，的半径为5，为等垂弦、的分割点，．求的长度；【问题解决】（3）、是的两条弦，，且，垂足为．①在图③中，利用直尺和圆规作弦（保留作图痕迹，不写作法）；②若的半径为，为常数），垂足与的位置关系随的值变化而变化，直接写出点与的位置关系及对应的的取值范围．【详解】证明：（1）如图②，连接，、，，，，，，，即，，，、是的等垂弦；（2）若点在内，如图，过点作，垂足为，作，垂足为，、是的等垂弦，，，四边形是矩形，，，，，，又，，，矩形为正方形，，，且，，在中，．即，解得：，；若点在外，如图，过点作，垂足为，作，垂足为，同理：，则；（3）①如图③，作直径，连接，作的角平分线，作的垂直平分线交的延长线于，过点作交于，，作的四等份线交于，，则弦即为所求；②如图，当点在上时，过点作，垂足为，作，垂足为，同理可证：四边形是矩形；，，，，，当时，点在上；当时，点在外；当时，点在内．