高一数学一隅三反系列(人教A版必修第一册)2.1等式与不等式的性质(精讲)(原卷版+解析)

这是一份高一数学一隅三反系列(人教A版必修第一册)2.1等式与不等式的性质(精讲)(原卷版+解析)，共17页。试卷主要包含了用不等式表示不等关系，实数式比较大小，不等式的性质，利用不等式求范围等内容，欢迎下载使用。


考点一 用不等式（组）表示不等关系
【例1-1】（2021·全国·高一课时练习）完成一项装修工程，请木工共需付工资每人400元，请瓦工共需付工资每人500元，现有工人工资预算不超过20 000元，设木工人，瓦工人，则工人满足的关系式是
A．B．C．D．
【例1-2】（2022·福建）有粮食和石油两种物资，可用轮船与飞机两种方式运输，每天每艘轮船和每架飞机的运输量如表：
现在要在一天内至少运输2000粮食和1 500石油.写出安排轮船艘数和飞机架数所满足的所有不等关系的不等式组.
【一隅三反】
1．（2022·江苏淮安）某公司准备对一项目进行投资，提出两个投资方案：方案为一次性投资万；方案 为第一年投资万，以后每年投资万.下列不等式表示“经过年之后，方案的投入不大于方案的投入”的是（ ）
A．B．
C．D．
2．（2022·山东）如图，在一块长为22m，宽为17m的矩形地面上，要修建同样宽的两条互相垂直的道路（两条道路分别与矩形的一条边平行），剩余部分种上草坪，使草坪的面积不小于300m2.设道路宽为xm，根据题意可列出的不等式为（ ）
A．B．
C．D．
3．（2022·青海）用不等式或不等式组表示下面的不等关系:
(1)某高速公路规定通过车辆的车货总高度h(单位:m)从地面算起不能超过4m;
(2)a与b的和是非负实数;
(3)如图,在一个面积小于的矩形地基的中心位置上建造一个仓库,仓库的四周建成绿地,仓库的长L(单位m)大于宽W(单位:m)的4倍.
考点二 实数式比较大小
【例2】（2022·江苏·高一）已知，，，则的大小关系为（ ）
A．B．C．D．无法确定
【一隅三反】
1．（2022·江苏·高一）若，，则与的大小关系为（ ）
A．B．C．D．不能确定
2．（2022·湖南·高一课时练习）若y1＝2x2－2x＋1，y2＝x2－4x－1，则y1与y2的大小关系是（ ）
A．y1>y2B．y1＝y2
C．y13．（2022·湖南·高一课时练习）已知0A．MN
C．M＝ND．无法确定
考点三 不等式的性质
【例3】（2022·江苏·高一）若，则下列说法正确的是（ ）
A．若，，则B．若，则
C．若，则D．若，则<
【一隅三反】
1．（2022·内蒙古）下列命题正确的是（ ）
A．若，则 B．若，则
C．若，则 D．若，则
2．（2022·浙江）（多选）下列命题是真命题的是（ ）
A．若，则
B．若，且，则
C．若，则
D．若，则
3．（2022·湖南张家界·高一期末）（多选）下列命题为真命题的是（ ）
A．若，则
B．若，，则
C．若，则
D．若，则
考点四 利用不等式求范围
【例4】（2022·江苏·高一）已知，，则的取值范围是（ ）
A．B．C．D．
【一隅三反】
1．（2022·江苏·高一）已知，则的取值范围为（ ）
A．B．C．D．
2．（2022·吉林延边·高一期末）已知，，则的取值范围是（ ）
A．B．
C．D．
3．（2022·山西太原·高一开学考试）已知，，则的取值范围是（ ）
A．B．C．D．
考点五 不等式的证明
【例5】（2022·湖南·高一课时练习）利用不等式的性质证明下列不等式：
(1)若，，则；
(2)若，，则．
【一隅三反】
1．（2022·浙江）证明下面的结论：
（1）如果，，且，那么；
（2）如果，，那么；
（3）如果，，那么；
（4）如果，，，那么.
2．（2021·福建·永安市第三中学高中校高一阶段练习）（1）求证：；
（2）求证：.轮船运输量
飞机运输量
粮食
300
150
石油
250
100
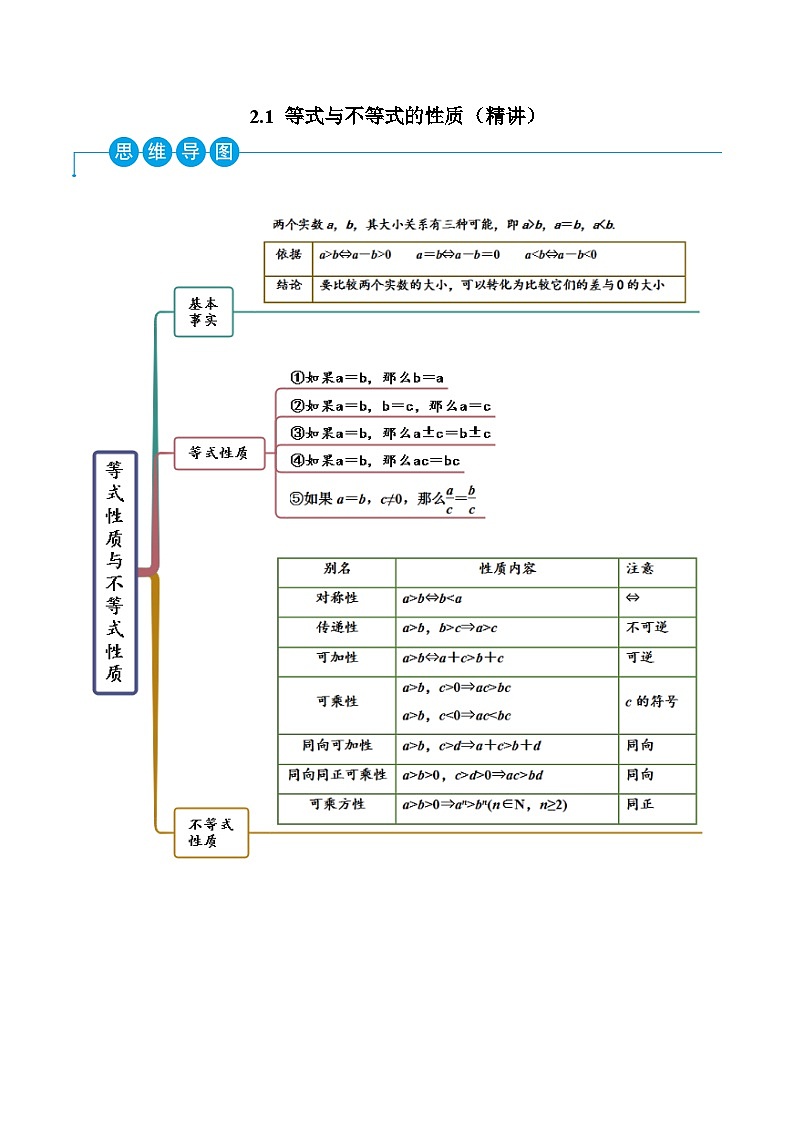
2.1 等式与不等式的性质（精讲）
考点一 用不等式（组）表示不等关系
【例1-1】（2021·全国·高一课时练习）完成一项装修工程，请木工共需付工资每人400元，请瓦工共需付工资每人500元，现有工人工资预算不超过20 000元，设木工人，瓦工人，则工人满足的关系式是
A．B．C．D．
【答案】A
【解析】由题意，可得，化简得，故正确答案为A.
【例1-2】（2022·福建）有粮食和石油两种物资，可用轮船与飞机两种方式运输，每天每艘轮船和每架飞机的运输量如表：
现在要在一天内至少运输2000粮食和1 500石油.写出安排轮船艘数和飞机架数所满足的所有不等关系的不等式组.
【答案】
【解析】设需安排艘轮船和架飞机，则，即.
【一隅三反】
1．（2022·江苏淮安）某公司准备对一项目进行投资，提出两个投资方案：方案为一次性投资万；方案 为第一年投资万，以后每年投资万.下列不等式表示“经过年之后，方案的投入不大于方案的投入”的是（ ）
A．B．
C．D．
【答案】D
【解析】经过年之后，方案的投入为，故经过年之后，方案的投入不大于方案的投入，即故选：D
2．（2022·山东）如图，在一块长为22m，宽为17m的矩形地面上，要修建同样宽的两条互相垂直的道路（两条道路分别与矩形的一条边平行），剩余部分种上草坪，使草坪的面积不小于300m2.设道路宽为xm，根据题意可列出的不等式为（ ）
A．B．
C．D．
【答案】B
【解析】把所修的两条道路分别平移到矩形的最上边和最左边，则剩下的草坪是一个长方形，
设道路的宽应为x米，草坪面积为（22﹣x）（17﹣x），
因为草坪的面积不小于300m2，所以(22－x)(17－x) 300，故选：B．
3．（2022·青海）用不等式或不等式组表示下面的不等关系:
(1)某高速公路规定通过车辆的车货总高度h(单位:m)从地面算起不能超过4m;
(2)a与b的和是非负实数;
(3)如图,在一个面积小于的矩形地基的中心位置上建造一个仓库,仓库的四周建成绿地,仓库的长L(单位m)大于宽W(单位:m)的4倍.
【答案】(1);(2);(3)
【解析】（1）；
（2）；
（3）由题,则矩形地基的长为,宽为,则
考点二 实数式比较大小
【例2】（2022·江苏·高一）已知，，，则的大小关系为（ ）
A．B．C．D．无法确定
【答案】B
【解析】，因为，所以，
又，所以，即.故选：B
【一隅三反】
1．（2022·江苏·高一）若，，则与的大小关系为（ ）
A．B．C．D．不能确定
【答案】B
【解析】因为，
所以，故选：B
2．（2022·湖南·高一课时练习）若y1＝2x2－2x＋1，y2＝x2－4x－1，则y1与y2的大小关系是（ ）
A．y1>y2B．y1＝y2
C．y1【答案】A
【解析】 ,故 ，故选：A
3．（2022·湖南·高一课时练习）已知0A．MN
C．M＝ND．无法确定
【答案】B
【解析】∵0∴M－N＝a1a2－(a1＋a2－1)＝a1a2－a1－a2＋1＝a1(a2－1)－(a2－1)＝(a1－1)(a2－1)>0，
∴M>N，故选：B.
考点三 不等式的性质
【例3】（2022·江苏·高一）若，则下列说法正确的是（ ）
A．若，，则B．若，则
C．若，则D．若，则<
【答案】C
【解析】对于A，若，则，所以A错误，
对于B，若，则，所以B错误，
对于C，因为，所以由不等式的性质可得，所以C正确，
对于D，因为，所以，所以，即，所以D错误，
故选：C
【一隅三反】
1．（2022·内蒙古）下列命题正确的是（ ）
A．若，则 B．若，则
C．若，则 D．若，则
【答案】D
【解析】对于A，若，由可得：，A错误；
对于B，若，则，此时未必成立，B错误；
对于C，当时，，C错误；
对于D，当时，由不等式性质知：，D正确.故选：D.
2．（2022·浙江）（多选）下列命题是真命题的是（ ）
A．若，则
B．若，且，则
C．若，则
D．若，则
【答案】BD
【解析】对于A，若，当时，，故A错误；
对于B，若，且，则，
所以，所以，故B正确；
对于C，若，当时，，故C错误；
对于D，若，
则，所以，故D正确.故选：BD.
3．（2022·湖南张家界·高一期末）（多选）下列命题为真命题的是（ ）
A．若，则
B．若，，则
C．若，则
D．若，则
【答案】ACD
【解析】由不等式性质知若，则，即，A对，
取，则，，，B错，
因为，所以，所以(当且仅当时等号成立)，而，故，C对，因为，所以，，所以，D对，
故选：ACD.
考点四 利用不等式求范围
【例4】（2022·江苏·高一）已知，，则的取值范围是（ ）
A．B．C．D．
【答案】D
【解析】因为，，所以，，所以，
所以的取值范围是，故选：D.
【一隅三反】
1．（2022·江苏·高一）已知，则的取值范围为（ ）
A．B．C．D．
【答案】C
【解析】，故，，得故选：C
2．（2022·吉林延边·高一期末）已知，，则的取值范围是（ ）
A．B．
C．D．
【答案】A
【解析】因为，所以，由，得.故选：A.
3．（2022·山西太原·高一开学考试）已知，，则的取值范围是（ ）
A．B．C．D．
【答案】D
【解析】设，，解得，
，
，，，
由不等式的性质可得，即，
因此，的取值范围是，故选D.
考点五 不等式的证明
【例5】（2022·湖南·高一课时练习）利用不等式的性质证明下列不等式：
(1)若，，则；
(2)若，，则．
【答案】(1)证明见解析(2)证明见解析
【解析】(1)证明： ，，又，；
(2)证明：，，又，．
【一隅三反】
1．（2022·浙江）证明下面的结论：
（1）如果，，且，那么；
（2）如果，，那么；
（3）如果，，那么；
（4）如果，，，那么.
【答案】见解析.
【解析】（1） ， ，则有；
（2） ， ，则有；
（3） ， ， ；
，，；
那么；
（4）由（3）可得，且，那么.
2．（2021·福建·永安市第三中学高中校高一阶段练习）（1）求证：；
（2）求证：.
【答案】（1）证明见解析；（2）证明见解析．
【解析】（1）∵，
∴；
（2）∵
，
当且仅当时等号成立，
∴轮船运输量
飞机运输量
粮食
300
150
石油
250
100