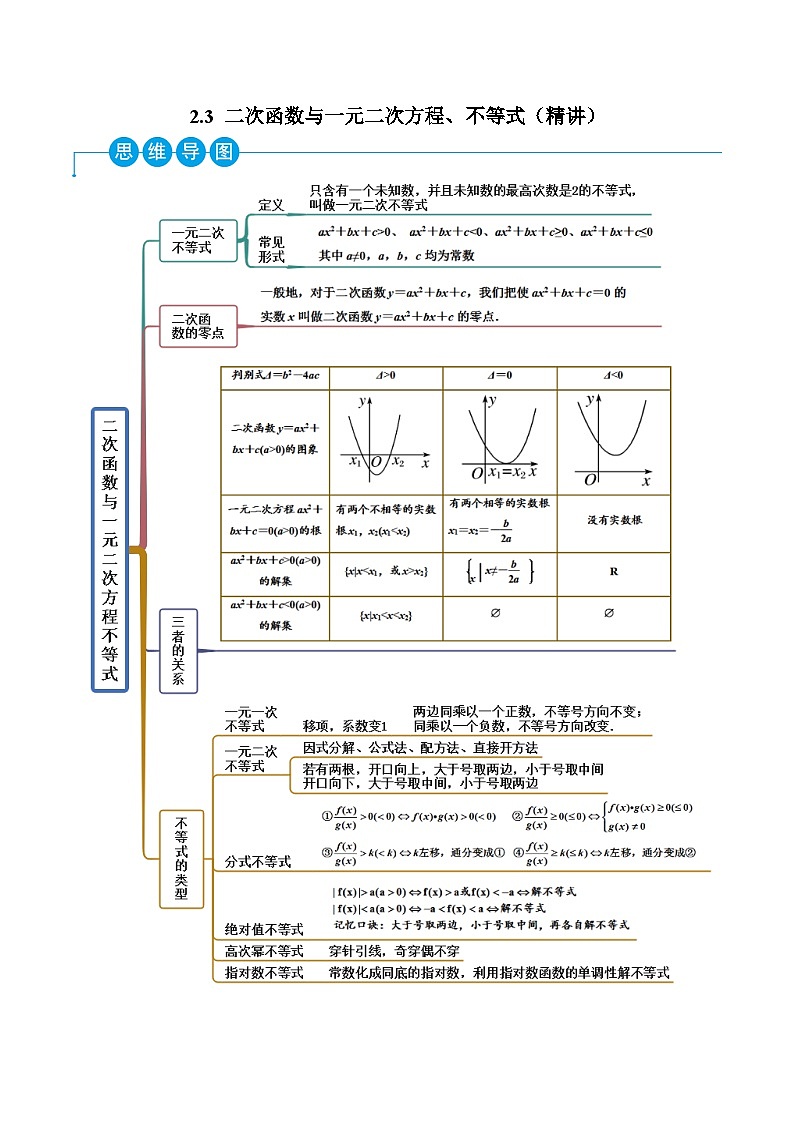
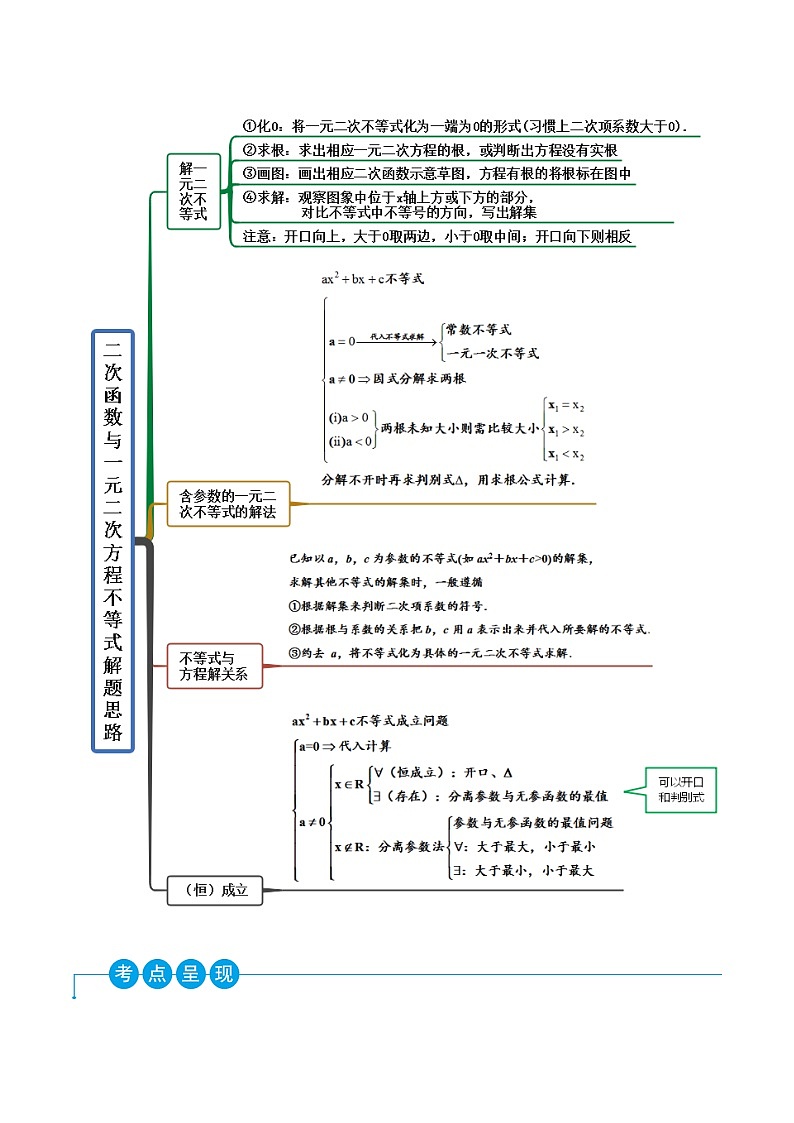
高一数学一隅三反系列(人教A版必修第一册)2.3二次函数与一元二次方程、不等式(精讲)(原卷版+解析)

这是一份高一数学一隅三反系列(人教A版必修第一册)2.3二次函数与一元二次方程、不等式(精讲)(原卷版+解析)，共24页。试卷主要包含了常见不等式的解法，三个一元二次的关系，一元二次根的相关问题，解含参的一元二次不等式，一元二次成立等内容，欢迎下载使用。


考点一 常见不等式的解法
【例1】（2022·浙江）求不等式的解集：
(1)；(2)；(3)；(4).
【一隅三反】
（2022·广西解下列不等式：
(1) ； (2) .(3)； (4)．
(5) ； (6) ；(7)；(8).
考点二 三个一元二次的关系
【例2-1】（2022·四川）已知不等式的解集为，则（ ）
A．B．C．D．
【例2-2】（2021·江苏南通·高一期中）已知不等式的解集为，则不等式的解集为（ ）
A．B．C．D．
【一隅三反】
1．（2022·广西）若不等式的解集是，则的值为（ ）
A．-10B．-14C．10D．14
2．（2022·江苏省）已知关于的一元二次不等式的解集为，则不等式的解集是（ ）
A．B．C．D．
3．（2022·山西）（多选）已知不等式的解集为或，则下列结论正确的是（ ）
A．B．
C．D．的解集为或
考点三 一元二次根的相关问题
【例3-1】（2022·甘肃）若一元二次方程的两根都是负数，求k的取值范围为___________.
【例3-2】（2021·全国·高一专题练习）已知方程有两个不相等的实数根，且两个实数根都大于2，则实数m的取值范围是（ ）
A．B．
C．D．
【例3-3】（2022·四川省高县中学校）已知关于的不等式的解集为，则的最小值是（ ）
A．B．C．D．
【例3-4】（2022·甘肃庆阳）关于x的方程恰有一根在区间内，则实数m的取值范围是（ ）
A．B．C．D．
【一隅三反】
1．（2022·北京海淀·高一期末）已知函数（b，c为实数），.若方程有两个正实数根，，则的最小值是（ ）
A．4B．2C．1D．
2．（2021·辽宁·沈阳市第一二〇中学高一期中）已知关于x的方程有两个正根，那么两个根的倒数和最小值是（ ）
A．-2B．C．D．1
3．（2022·上海）若关于x的方程的一根大于－1，另一根小于－1，则实数k的取值范围为______．
4．（2022·辽宁·高一阶段练习）已知一元二次方程x2＋ax＋1＝0的一个根在(0，1)内，另一个根在(1，2)内，则实数a的取值范围为________．
考点四 解含参的一元二次不等式
【例4-1】（2022·甘肃定西）若关于x的不等式的解集中恰有3个整数，则实数m的取值范围为（ ）
A．B．C．D．
【例4-2】（2022·浙江·桐乡市凤鸣高级中学）已知关于的不等式.
(1)若不等式的解集为，求实数、的值；
(2)若，求此不等式的解集.
【一隅三反】
1．（2021·甘肃）已知关于x的不等式的解集为M，若，则a的取值范围为（ ）
A．[－2，4]B．（－2，4）
C．D．
2．（2022·全国·专题练习）若关于的不等式的解集中恰有3个正整数，则实数的取值范围为___________．
3．（2021·全国·高一课时练习）解关于的一元二次不等式，其中．
4．（2022·北京市第五中学高一阶段练习）请回答下列问题：
(1)若关于的不等式的解集为或，求，的值.
(2)求关于的不等式的解集.
考点五 一元二次（恒）成立
【例5-1】（2022·广东）已知关于的不等式对任意恒成立，则的取值范围是（ ）
A．B．C．或D．或
【例5-2】（2022·河南·濮阳）已知当时，恒成立，则实数的取值范围是（ ）
A．B．
C．D．
【例5-3】（2022·黑龙江齐齐哈尔）若命题“”为假命题，则实数x的取值范围为（ ）
A．B．C．D．
【例5-4】（2022·山西）已知关于的不等式在上有解，则实数的取值范围是（ ）
A．B．C．D．
【一隅三反】
1．（2022·海南·嘉积中学）对任意的，恒成立，则的取值范围为（ ）
A．B．C．D．
2．（2022·浙江金华第一中学高一阶段练习）一元二次不等式对一切实数恒成立，则的取值范围是（ ）
A．B．C．D．
3．（2022·陕西·长安一中高一阶段练习）若不等式对一切实数均成立，则实数的取值范围是（ ）
A．B．C．D．
4．（2022·江苏）若关于的不等式有解，则实数a的取值范围是____________．
5．（2022·湖北）关于的不等式在内有解，则的取值范围为________．
2.3 二次函数与一元二次方程、不等式（精讲）
考点一 常见不等式的解法
【例1】（2022·浙江）求不等式的解集：
(1)；(2)；(3)；(4).
【答案】(1)或；(2)；(3)或；(4).
【解析】（1）由，得，解得或，故不等式的解集为或；
(2)由得，，故不等式的解集为；
(3)由可得，，解得或，故不等式的解集为或；
(4)由，可得，∴，解得，故不等式的解集为.
【一隅三反】
（2022·广西解下列不等式：
(1) ； (2) .(3)； (4)．
(5) ； (6) ；(7)；(8).
【答案】(1)(2)(3)；(4)
.(5)或(6)(7)(8)
【解析】(1)由题，即，解得或，即；
(2)由题，解得或，即
(3)不等式化为：，解得，所以的解集为.
(4)，原不等式化为：，解得：，
所以的解集是.
(5)因为，
所以方程有两个不等实根 ，.
又二次函数的图象开口向上，所以原不等式的解集为或
(6)因为，
所以方程有两个不等实根，即，.
又二次函数的图象开口向下，所以原不等式的解集为．
(7)可得，∴∴该不等式解集为；
(8)原不等式，∴，∴该不等式解集为；
考点二 三个一元二次的关系
【例2-1】（2022·四川）已知不等式的解集为，则（ ）
A．B．C．D．
【答案】A
【解析】由不等式的解集知：和是方程的两根，.故选：A.
【例2-2】（2021·江苏南通·高一期中）已知不等式的解集为，则不等式的解集为（ ）
A．B．C．D．
【答案】A
【解析】关于x的不等式的解集为
，且和1是方程的两个根，则，，
关于x的不等式，即，，解得，
故不等式的解集为，故选：A
【一隅三反】
1．（2022·广西）若不等式的解集是，则的值为（ ）
A．-10B．-14C．10D．14
【答案】B
【解析】由题意，和是方程的两个根，由韦达定理得：且，解得：，，所以.故选：B
2．（2022·江苏省）已知关于的一元二次不等式的解集为，则不等式的解集是（ ）
A．B．C．D．
【答案】A
【解析】不等式的解集是，所以方程的解是和，且，
则，解得，，所以不等式化为，即，解得，所以，所求不等式的解集是．故选：A．
3．（2022·山西）（多选）已知不等式的解集为或，则下列结论正确的是（ ）
A．B．
C．D．的解集为或
【答案】ABC
【解析】根据二次函数开口与二次不等式之间的关系可知，A正确；
的根为，则，即∴，B正确；
，C正确；，即，则，解得
∴的解集为，D错误；故选：ABC．
考点三 一元二次根的相关问题
【例3-1】（2022·甘肃）若一元二次方程的两根都是负数，求k的取值范围为___________.
【答案】
【解析】首先，设方程的两根为，则，
所以，又，解得．故答案为：．
【例3-2】（2021·全国·高一专题练习）已知方程有两个不相等的实数根，且两个实数根都大于2，则实数m的取值范围是（ ）
A．B．
C．D．
【答案】C
【解析】令
由题可知：
则，即故选：C
【例3-3】（2022·四川省高县中学校）已知关于的不等式的解集为，则的最小值是（ ）
A．B．C．D．
【答案】C
【解析】由题设，，且，
所以，当且仅当时等号成立.故选：C
【例3-4】（2022·甘肃庆阳）关于x的方程恰有一根在区间内，则实数m的取值范围是（ ）
A．B．C．D．
【答案】D
【解析】方程对应的二次函数设为：
因为方程恰有一根属于，则需要满足：
①，，解得：；
②函数刚好经过点或者，另一个零点属于，
把点代入，解得：，
此时方程为，两根为，，而，不合题意，舍去
把点代入，解得：，
此时方程为，两根为，，而，故符合题意；
③函数与x轴只有一个交点，横坐标属于，
，解得，
当时，方程的根为，不合题意；
若，方程的根为，符合题意
综上：实数m的取值范围为故选：D
【一隅三反】
1．（2022·北京海淀·高一期末）已知函数（b，c为实数），.若方程有两个正实数根，，则的最小值是（ ）
A．4B．2C．1D．
【答案】B
【解析】因为函数（b，c为实数），，所以，
解得，所以，
因为方程有两个正实数根，，所以，解得，
所以，当c=2时，等号成立，所以其最小值是2，故选：B
2．（2021·辽宁·沈阳市第一二〇中学高一期中）已知关于x的方程有两个正根，那么两个根的倒数和最小值是（ ）
A．-2B．C．D．1
【答案】B
【解析】由题意可得，解得或，
设两个为，，由两根为正根可得，解得，综上知，.
故两个根的倒数和为，
，，，故，，故两个根的倒数和的最小值是.故选：B
3．（2022·上海）若关于x的方程的一根大于－1，另一根小于－1，则实数k的取值范围为______．
【答案】
【解析】由题意，关于的方程的一根大于-1，另一根小于-1，
设，根据二次函数的性质，可得，解得，
所以实数的取值范围为.故答案为：.
4．（2022·辽宁·高一阶段练习）已知一元二次方程x2＋ax＋1＝0的一个根在(0，1)内，另一个根在(1，2)内，则实数a的取值范围为________．
【答案】
【解析】设f (x)＝x2＋ax＋1，由题意知，解得－考点四 解含参的一元二次不等式
【例4-1】（2022·甘肃定西）若关于x的不等式的解集中恰有3个整数，则实数m的取值范围为（ ）
A．B．C．D．
【答案】C
【解析】不等式，即，
当时，不等式解集为，此时要使解集中恰有3个整数，这3个整数只能是4，5，6，故；
当时，不等式解集为，此时不符合题意；
当时，不等式解集为，此时要使解集中恰有3个整数，这3个整数只能是0，1，2，故；
故实数m的取值范围为．故选：C
【例4-2】（2022·浙江·桐乡市凤鸣高级中学）已知关于的不等式.
(1)若不等式的解集为，求实数、的值；
(2)若，求此不等式的解集.
【答案】(1)，(2)答案见解析
【解析】(1)由题意可知，关于的方程的两根分别为、，所以，，
由韦达定理可得，解得.
(2)因为，原不等式即为.
当时，原不等式即为，解得；
当时，方程的两个根分别为、.
①当时，解不等式可得或；
②当时，若时，即，即时，
解不等式可得；
若时，即当时，原不等式即为，即，原不等式的解集为；
若时，即，即当时，解不等式可得.
综上所述，当时，原不等式的解集为；
当时，原不等式的解集为；
当时，原不等式的解集为；
当时，原不等式的解集为；
当时，原不等式的解集为或.
【一隅三反】
1．（2021·甘肃）已知关于x的不等式的解集为M，若，则a的取值范围为（ ）
A．[－2，4]B．（－2，4）
C．D．
【答案】A
【解析】由于，所以，即，解得，
所以的取值范围是.故选：A
2．（2022·全国·专题练习）若关于的不等式的解集中恰有3个正整数，则实数的取值范围为___________．
【答案】，
【解析】可化为，该不等式的解集中恰有3个正整数，
不等式的解集为，且；故答案为：，．
3．（2021·全国·高一课时练习）解关于的一元二次不等式，其中．
【答案】答案见解析
【解析】原不等式整理得，由于，进而得．
当时，原不等式即为，原不等式的解集为；
当时，，原不等式的解集为；
当时，，原不等式的解集为．
综上所述，当时，原不等式的解集为；
当时，原不等式的解集为；
当时，原不等式的解集为．
4．（2022·北京市第五中学高一阶段练习）请回答下列问题：
(1)若关于的不等式的解集为或，求，的值.
(2)求关于的不等式的解集.
【答案】(1)、(2)答案见解析
【解析】(1)因为关于的不等式的解集为或，所以和为方程的两根，所以，解得；
(2)不等式，即，即，
当时，原不等式解集为；
当时，方程的根为，，
①当时，，原不等式的解集为或；
②当时，，原不等式的解集为；
③当时，，原不等式的解集为；
④当时，，原不等式的解集为
考点五 一元二次（恒）成立
【例5-1】（2022·广东）已知关于的不等式对任意恒成立，则的取值范围是（ ）
A．B．C．或D．或
【答案】B
【解析】当时，恒成立，符合题意；
当时，由题意有，解得，综上，.故选：B.
【例5-2】（2022·河南·濮阳）已知当时，恒成立，则实数的取值范围是（ ）
A．B．
C．D．
【答案】D
【解析】恒成立，即，对任意得恒成立，
令，，当时，，不符题意，故，
当时，函数在上递增，则，
解得或（舍去），当时，函数在上递减，
则，解得或（舍去），
综上所述，实数的取值范围是.故选：D.
【例5-3】（2022·黑龙江齐齐哈尔）若命题“”为假命题，则实数x的取值范围为（ ）
A．B．C．D．
【答案】C
【解析】命题“”为假命题，其否定为真命题，
即“”为真命题．令，
则，即，解得，所以实数x的取值范围为.故选：C
【例5-4】（2022·山西）已知关于的不等式在上有解，则实数的取值范围是（ ）
A．B．C．D．
【答案】A
【解析】由题意得，，，即 ，故问题转化为在上有解，
设，则，，对于 ，当且仅当时取等号，
则，故 ，故选：A
【一隅三反】
1．（2022·海南·嘉积中学）对任意的，恒成立，则的取值范围为（ ）
A．B．C．D．
【答案】D
【解析】当时，由得：，
（当且仅当，即时取等号），，解得：，
即的取值范围为.故选：D.
2．（2022·浙江金华第一中学高一阶段练习）一元二次不等式对一切实数恒成立，则的取值范围是（ ）
A．B．C．D．
【答案】B
【解析】由题，一元二次不等式对一切实数恒成立则 ，即，解得故选：B
3．（2022·陕西·长安一中高一阶段练习）若不等式对一切实数均成立，则实数的取值范围是（ ）
A．B．C．D．
【答案】A
【解析】因为恒成立所以恒成立
恒成立恒成立
故解之得：故选：A
4．（2022·江苏）若关于的不等式有解，则实数a的取值范围是____________．
【答案】
【解析】当时，不等式为有解，故，满足题意；
当时，若不等式有解，
则满足，解得或；
当时，此时对应的函数的图象开口向下，此时不等式总是有解，所以，
综上可得，实数a的取值范围是.
5．（2022·湖北）关于的不等式在内有解，则的取值范围为________．
【答案】
【解析】在内有解，，其中；
设，则当时，，
，解得：，的取值范围为.故答案为：.