

高一数学一隅三反系列(人教A版必修第一册)3.4函数的应用(一)(精练)(原卷版+解析)
展开1.(2022福建)一个矩形的周长是20,矩形的长y关于宽x的函数解析式为( )(默认y>x)
A.y=10-x(0
(1)设MP=x米,PN=y米,将y表示成x的函数,求该函数的解析式及定义域;
(2)求矩形BNPM面积的最大值.
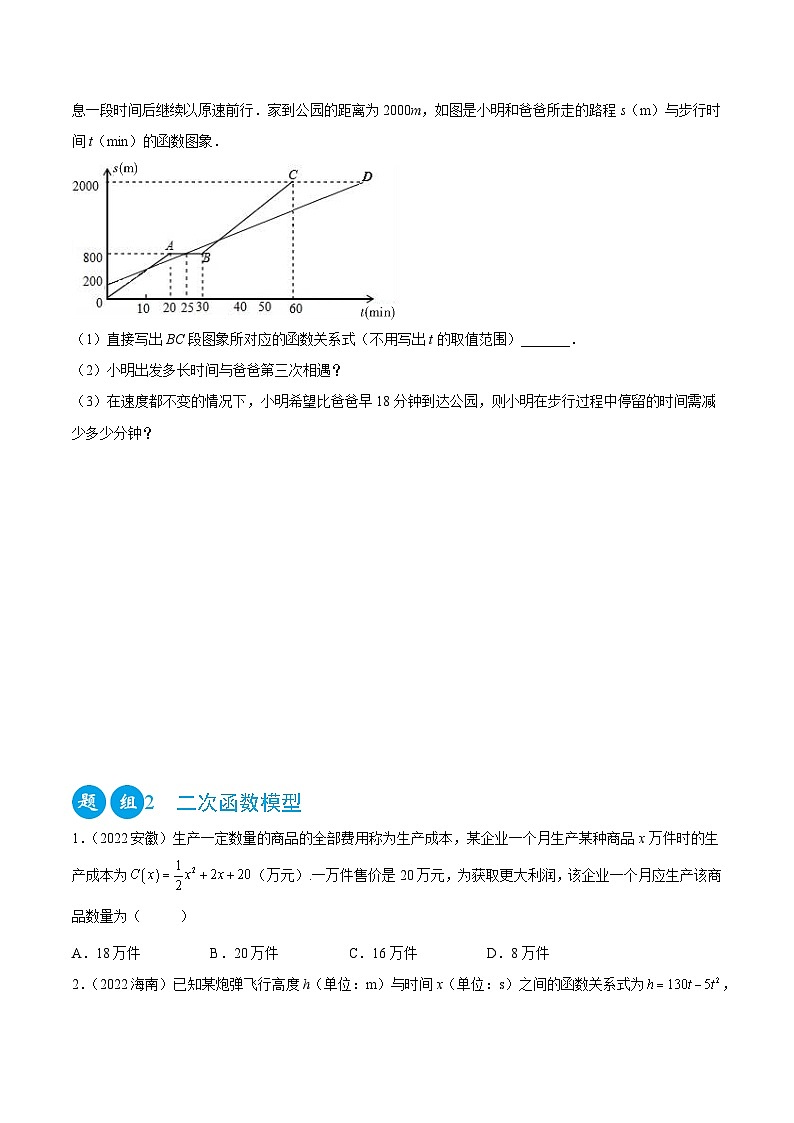
3.(2022北京)小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发匀速前行,且途中休息一段时间后继续以原速前行.家到公园的距离为2000m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
(1)直接写出BC段图象所对应的函数关系式(不用写出t的取值范围)_______.
(2)小明出发多长时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早18分钟到达公园,则小明在步行过程中停留的时间需减少多少分钟?
2 二次函数模型
1.(2022安徽)生产一定数量的商品的全部费用称为生产成本,某企业一个月生产某种商品x万件时的生产成本为(万元).一万件售价是20万元,为获取更大利润,该企业一个月应生产该商品数量为( )
A.18万件B.20万件C.16万件D.8万件
2.(2022海南)已知某炮弹飞行高度h(单位:m)与时间x(单位:s)之间的函数关系式为,则炮弹飞行高度高于的时间长为( )
A.B.C.D.
3.(2022山东)某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,二次函数图象(部分)刻画了该公司年初以来累积利润(万元)与销售时间(月)之间的关系(即前个月的利润总和与之间的关系).根据图象提供的信息解答下列问题:
(1)由已知图象上的三点坐标,求累积利润(万元)与时间(月)之间的函数关系式;
(2)求截止到第几个月末公司累积利润可达到万元;
(3)求第八个月公司所获得的利润.
4(2021·全国·高一专题练习)为鼓励大学毕业生自主创业,某市出台了相关政策,由政府协调,企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.某大学毕业生校照相关政策投资销售一种新型节能灯,已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月的销售量(单位:件)与销售单价(单位:元)之间的关系近似满足一次函数: .
(1)设他每月获得的利润为 (单位:元),写出他每月获得的利润与销售单价x的函数关系式,并求出利润的最大值.
(2)相关部门规定,这种节能灯的销售单价不得高于元.如果他想要每月获得的利润不少于元,那么政府每个月为他承担的总差价的取值范围是多少?
3 分段函数模型
1.(2022河南)某公司生产一种产品的固定成本为0.5万元,但每生产100件需要增加投入0.25万元,市场对此产品的需求量为500件,销售收入为函数R(x)=5x-(0≤x≤5)万元,其中x是产品售出的数量(单位:百件).
(1)把利润表示为年产量的函数f(x);
(2)年产量为多少时,当年公司所得利润最大?
2.(2022·湖南)十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划,年某企业计划引进新能源汽车生产设备看,通过市场分析,全年需投入固定成本万元,每生产(百辆)需另投入成本(万元),且.由市场调研知,每辆车售价万元,且全年内生产的车辆当年能全部销售完.
(1)求出年的利润(万元)关于年产量(百辆)的函数关系式;(利润=销售额—成本)
(2)当年产量为多少百辆时,企业所获利润最大?并求出最大利润.
3.(2022河南)年初,新冠肺炎疫情袭击全国,对人民生命安全和生产生活造成严重影响.为降低疫情影响,某厂家拟尽快加大力度促进生产.已知该厂家生产某种产品的年固定成本为万元,每生产千件,需另投入成本为,当年产量不足千件时,(万元).当年产量不小于千件时,(万元).每件商品售价为万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润(万元)关于年产量(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?最大利润是多少?
4 基本不等式模型
1.(2022·全国·高一课时练习)近年来,中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们抵制华为,然而这并没有让华为却步.华为在年不仅净利润创下记录,海外增长同样强劲.今年,我国华为某一企业为了进一步增加市场竞争力,计划在年利用新技术生产某款新手机,通过市场分析,生产此款手机全年需投入固定成本万,每生产(千部)手机,需另投入成本万元,且.由市场调研知,每部手机售价万元,且全年内生产的手机当年能全部销售完.
(1)求出年的利润(万元)关于年产量(千部)的函数解析式(利润销售额成本);
(2)年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
2.(2022·江苏)某汽车公司购买了辆大客车用于长途客运,每辆万元,预计每辆客车每年收入约万元,每辆客车第一年各种费用约为万元,从第二年开始每年比上一年所需费用要增加万元.
(1)写出辆客车运营的总利润(万元)与运营年数的函数关系式:
(2)这辆客车运营多少年,可使年平均运营利润最大?最大利润是多少?
3.(2022·山西大附中)小李同学大学毕业后,决定利用所学专业进行自主创业.经过调查,生产某小型电子产品需投入年固定成本5万元,每年生产x万件,需另投入流动成本万元,在年产量不足8万件时,(万元);在年产量不小于8万件时,(万元).每件产品售价为10元,经分析,生产的产品当年能全部售完.
(1)写出年利润(万元)关于年产量x(万件)的函数解析式.(年利润=年销售收入-固定成本-流动成本)
(2)年产量为多少万件时,小李在这一产品的生产中所获利润最大?最大利润是多少?
4.(2022·全国·高一课时练习)2022年第24届北京冬季奥林匹克运动会,于2022年2月4日星期五开幕,将于2月20日星期日闭幕.该奥运会激发了大家对冰雪运动的热情,与冰雪运动有关的商品销量持续增长.对某店铺某款冰雪运动装备在过去的一个月内(以30天计)的销售情况进行调查发现:该款冰雪运动装备的日销售单价(元/套)与时间x(被调查的一个月内的第x天)的函数关系近似满足(k为正常数).该商品的日销售量(个)与时间x(天)部分数据如下表所示:
已知第10天该商品的日销售收入为121元.
(1)求k的值;
(2)给出两种函数模型:①,②,请你根据上表中的数据,从中选择你认为最合适的一种函数来描述该商品的日销售量与时间x的关系,并求出该函数的解析式;
(3)求该商品的日销售收入(,)(元)的最小值.x
10
20
25
30
110
120
125
120
3.4 函数的应用(一)(精练)
1 一次函数模型
1.(2022福建)一个矩形的周长是20,矩形的长y关于宽x的函数解析式为( )(默认y>x)
A.y=10-x(0
【解析】由题意可知2y+2x=20,即y=10-x,又10-x>x,所以0
2.(2022上海)如图所示,已知边长为8米的正方形钢板有一个角被锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.
(1)设MP=x米,PN=y米,将y表示成x的函数,求该函数的解析式及定义域;
(2)求矩形BNPM面积的最大值.
【答案】(1);(2)48.
【解析】(1)如图所示,延长NP交AF于点Q,
所以PQ=8-y,EQ=x-4.
在中, ,所以.
所以,定义域为.
(2)设矩形BNPM的面积为S,
则,开口向下,且对称轴为,则在上单调递增,所以当x=8时,S取最大值48,所以矩形BNPM面积的最大值为48.
3.(2022北京)小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发匀速前行,且途中休息一段时间后继续以原速前行.家到公园的距离为2000m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
(1)直接写出BC段图象所对应的函数关系式(不用写出t的取值范围)_______.
(2)小明出发多长时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早18分钟到达公园,则小明在步行过程中停留的时间需减少多少分钟?
【答案】(1) s=40t–400 (2) 37.5min (3) 3min
【解析】(1)设直线BC所对应的函数表达式为s=kt+b,
将(30,800),(60,2000)代入得,
,解得,
∴直线BC所对应的函数表达式为s=40t–400.
(2)设小明的爸爸所走路程s与时间t的函数关系式为s=mt+n,
则,解得.
即小明的爸爸所走路程s与时间t的函数关系式是s=24t+200,
解方程组,得,
即小明出发37.5min时与爸爸第三次相遇.
(3)当s=2000时,2000=24t+200,得t=75,
∵75–60=15,
∴小明希望比爸爸早18 min到达公园,
则小明在步行过程中停留的时间需要减少3min.
2 二次函数模型
1.(2022安徽)生产一定数量的商品的全部费用称为生产成本,某企业一个月生产某种商品x万件时的生产成本为(万元).一万件售价是20万元,为获取更大利润,该企业一个月应生产该商品数量为( )
A.18万件B.20万件C.16万件D.8万件
【答案】A
【解析】利润.
所以当时,L(x)有最大值.故选:A
2.(2022海南)已知某炮弹飞行高度h(单位:m)与时间x(单位:s)之间的函数关系式为,则炮弹飞行高度高于的时间长为( )
A.B.C.D.
【答案】A
【解析】根据题意可得,解得,则炮弹飞行高度高于的时间长为(s).
故选:A.
3.(2022山东)某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,二次函数图象(部分)刻画了该公司年初以来累积利润(万元)与销售时间(月)之间的关系(即前个月的利润总和与之间的关系).根据图象提供的信息解答下列问题:
(1)由已知图象上的三点坐标,求累积利润(万元)与时间(月)之间的函数关系式;
(2)求截止到第几个月末公司累积利润可达到万元;
(3)求第八个月公司所获得的利润.
【答案】(1);(2)第十个月;(3)利润为万元.
【解析】(1)设与的函数关系式为.
由题中函数图象过点、、,得,解得,
因此,所求函数关系式为;
(2)把代入,得,整理得,
,解得,
因此,截止到第十个月末公司累积利润可达到万元;
(3)第八个月公司所获得的利润为(万元).
因此,第八个月公司所获得的利润为万元.
4(2021·全国·高一专题练习)为鼓励大学毕业生自主创业,某市出台了相关政策,由政府协调,企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.某大学毕业生校照相关政策投资销售一种新型节能灯,已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月的销售量(单位:件)与销售单价(单位:元)之间的关系近似满足一次函数: .
(1)设他每月获得的利润为 (单位:元),写出他每月获得的利润与销售单价x的函数关系式,并求出利润的最大值.
(2)相关部门规定,这种节能灯的销售单价不得高于元.如果他想要每月获得的利润不少于元,那么政府每个月为他承担的总差价的取值范围是多少?
【答案】(1),;(2).
【解析】(1)依题意可得:每件的销售利润为元,每月的销售量为件,
所以每月获得的利润与销售单价x的函数关系式为:
,
对称轴为,开口向下,此时最大值为,
所以利润与销售单价x的函数关系式,最大利润为元.
(2)由每月获得的利润不小于元,
得,
即 ,解得:,
这种节能灯的销售单价不得高于元,所以,
设政府每个月为他承担的总差价为元,
则,
由可得,
所以政府每个月为他承担的总差价的取值范围是元.
3 分段函数模型
1.(2022河南)某公司生产一种产品的固定成本为0.5万元,但每生产100件需要增加投入0.25万元,市场对此产品的需求量为500件,销售收入为函数R(x)=5x-(0≤x≤5)万元,其中x是产品售出的数量(单位:百件).
(1)把利润表示为年产量的函数f(x);
(2)年产量为多少时,当年公司所得利润最大?
【答案】(1)f(x)=;
(2)475件.
【解析】(1)产量为x(百件),
当0≤x≤5时,f(x)=5x--(0.5+0.25x);
当x>5时,销售收入为万元,此时f(x)=-(0.5+0.25x)=12-0.25x;
∴f(x)=;
(2)当0≤x≤5时,f(x)=+10.78125;
当x>5时,函数f(x)为单调递减函数.
∴当x=4.75时,即年产量为475件时,公司所得利润最大.
2.(2022·湖南)十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划,年某企业计划引进新能源汽车生产设备看,通过市场分析,全年需投入固定成本万元,每生产(百辆)需另投入成本(万元),且.由市场调研知,每辆车售价万元,且全年内生产的车辆当年能全部销售完.
(1)求出年的利润(万元)关于年产量(百辆)的函数关系式;(利润=销售额—成本)
(2)当年产量为多少百辆时,企业所获利润最大?并求出最大利润.
【答案】(1)
(2)百辆,最大利润为万
【解析】(1)由题意得当时,,当时,,所以,
(2)由(1)得当时,,当时,,当时, ,当且仅当,即时等号成立,,时,,,时,即年产量为百辆时,企业所获利润最大,且最大利润为万元.
3.(2022河南)年初,新冠肺炎疫情袭击全国,对人民生命安全和生产生活造成严重影响.为降低疫情影响,某厂家拟尽快加大力度促进生产.已知该厂家生产某种产品的年固定成本为万元,每生产千件,需另投入成本为,当年产量不足千件时,(万元).当年产量不小于千件时,(万元).每件商品售价为万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润(万元)关于年产量(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?最大利润是多少?
【答案】(1);(2)当年产量为千件时,该厂在这一商品生产中所获利润最大,最大利润为万元.
【解析】(1)因为每件商品售价为万元,则千件商品销售额为万元,
依题意得:
当时,,
当时,,
所以;
(2)当时,,
此时,当时,即万元.
当时,,
此时,即万元,
由于,
所以当年产量为千件时,该厂在这一商品生产中所获利润最大,最大利润为万元.
4 基本不等式模型
1.(2022·全国·高一课时练习)近年来,中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们抵制华为,然而这并没有让华为却步.华为在年不仅净利润创下记录,海外增长同样强劲.今年,我国华为某一企业为了进一步增加市场竞争力,计划在年利用新技术生产某款新手机,通过市场分析,生产此款手机全年需投入固定成本万,每生产(千部)手机,需另投入成本万元,且.由市场调研知,每部手机售价万元,且全年内生产的手机当年能全部销售完.
(1)求出年的利润(万元)关于年产量(千部)的函数解析式(利润销售额成本);
(2)年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
【答案】(1);
(2)年产量为(千部)手机时,企业利润最大,最大利润为万元.
【解析】(1)由题意知:每生产(千部)手机,投入的成本,
,
即;
(2)①当时,,
当时,;
②当时,(当且仅当,即时取等号),;
综上所述:年产量为(千部)手机时,企业利润最大,最大利润为万元.
2.(2022·江苏)某汽车公司购买了辆大客车用于长途客运,每辆万元,预计每辆客车每年收入约万元,每辆客车第一年各种费用约为万元,从第二年开始每年比上一年所需费用要增加万元.
(1)写出辆客车运营的总利润(万元)与运营年数的函数关系式:
(2)这辆客车运营多少年,可使年平均运营利润最大?最大利润是多少?
【答案】(1);(2)这4辆客车运营年,可使年平均运营利润最大,最大利润为48万元.
【解析】(1)依题意得,每辆车年总收入为万元,
总支出为,
所以辆客车运营的总利润.
(2)年平均运营利润为,
因为,所以,当且仅当时,等号成立,
此时,
所以这4辆客车运营年,可使年平均运营利润最大,最大利润为48万元.
3.(2022·山西大附中)小李同学大学毕业后,决定利用所学专业进行自主创业.经过调查,生产某小型电子产品需投入年固定成本5万元,每年生产x万件,需另投入流动成本万元,在年产量不足8万件时,(万元);在年产量不小于8万件时,(万元).每件产品售价为10元,经分析,生产的产品当年能全部售完.
(1)写出年利润(万元)关于年产量x(万件)的函数解析式.(年利润=年销售收入-固定成本-流动成本)
(2)年产量为多少万件时,小李在这一产品的生产中所获利润最大?最大利润是多少?
【答案】(1)
(2)当年产量为8万件时,小李在这一产品的生产中所获利润最大,最大利润为万元.
【解析】(1)解:因为每件产品售价为10元,所以x万件产品销售收入为万元.
依题意得,当时,;
当时,.
所以;
(2)当时,,
当时,取得最大值;
当时,由双勾函数的单调性可知,函数在区间上为减函数.
当时,取得最大值.
由,则可知当年产量为8万件时,小李在这一产品的生产中所获利润最大,
最大利润为万元.
4.(2022·全国·高一课时练习)2022年第24届北京冬季奥林匹克运动会,于2022年2月4日星期五开幕,将于2月20日星期日闭幕.该奥运会激发了大家对冰雪运动的热情,与冰雪运动有关的商品销量持续增长.对某店铺某款冰雪运动装备在过去的一个月内(以30天计)的销售情况进行调查发现:该款冰雪运动装备的日销售单价(元/套)与时间x(被调查的一个月内的第x天)的函数关系近似满足(k为正常数).该商品的日销售量(个)与时间x(天)部分数据如下表所示:
已知第10天该商品的日销售收入为121元.
(1)求k的值;
(2)给出两种函数模型:①,②,请你根据上表中的数据,从中选择你认为最合适的一种函数来描述该商品的日销售量与时间x的关系,并求出该函数的解析式;
(3)求该商品的日销售收入(,)(元)的最小值.
【答案】(1)
(2)选择②,,(,)
(3)121元
【解析】(1)因为第10天该商品的日销售收入为121元,所以,解得;
(2)由表中数据可得,当时间变化时,该商品的日销售量有增有减,并不单调,
故只能选②:
代入数据可得:,解得,,
所以,(,)
(3)由(2)可得,,
所以,,
所以当,时,在区间上单调递减,在区间上单调递增,
所以当时,有最小值,且为121;
当,时,为单调递减函数,
所以当时,有最小值,且为124,
综上,当时,有最小值,且为121元,
所以该商品的日销售收入最小值为121元.x
10
20
25
30
110
120
125
120
高一数学一隅三反系列(人教A版必修第一册)3.3幂函数(精练)(原卷版+解析): 这是一份高一数学一隅三反系列(人教A版必修第一册)3.3幂函数(精练)(原卷版+解析),共18页。试卷主要包含了给出下列函数等内容,欢迎下载使用。
高一数学一隅三反系列(人教A版必修第一册)3.2.2函数的奇偶性(精练)(原卷版+解析): 这是一份高一数学一隅三反系列(人教A版必修第一册)3.2.2函数的奇偶性(精练)(原卷版+解析),共23页。试卷主要包含了判断下列函数的奇偶性,函数是定义在上的奇函数,且等内容,欢迎下载使用。
高一数学一隅三反系列(人教A版必修第一册)3.2.1函数的单调性(精练)(原卷版+解析): 这是一份高一数学一隅三反系列(人教A版必修第一册)3.2.1函数的单调性(精练)(原卷版+解析),共32页。试卷主要包含了已知函数,已知,,,已知函数其中为常数且满足,已知函数.完成下面两个问题,已知函数.等内容,欢迎下载使用。












