高一数学一隅三反系列(人教A版必修第一册)4.3对数运算(精讲)(原卷版+解析)

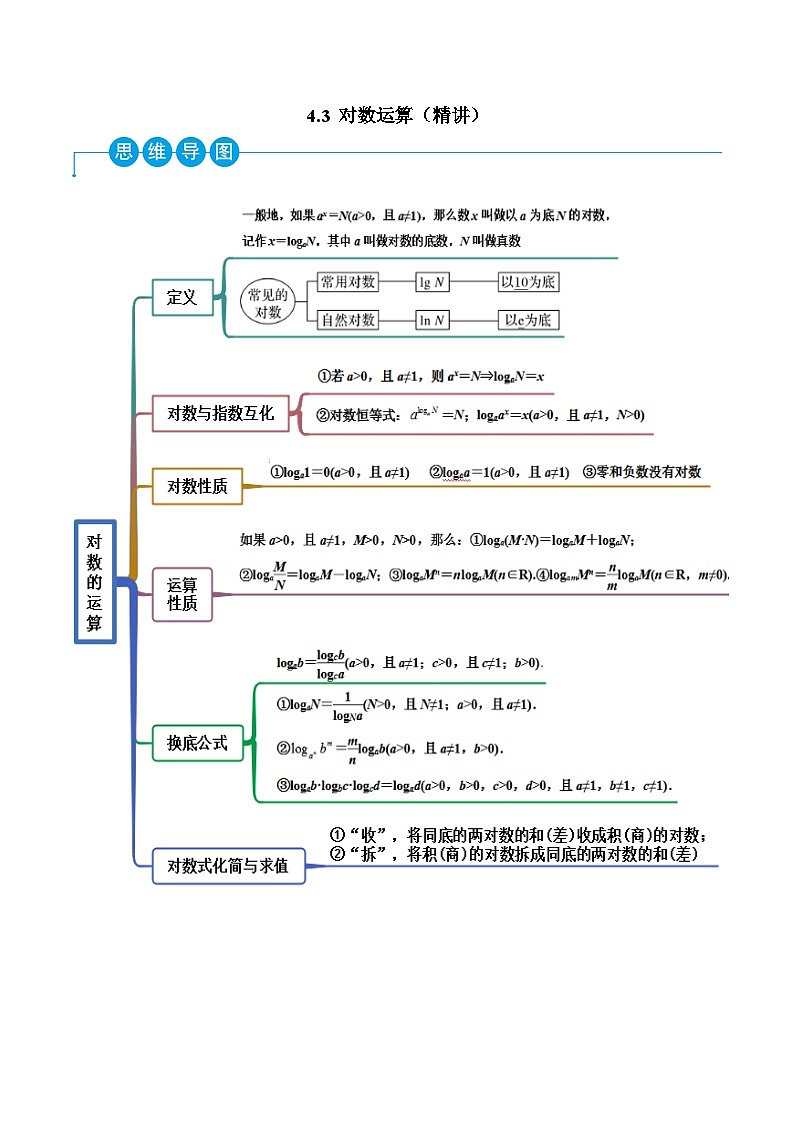
这是一份高一数学一隅三反系列(人教A版必修第一册)4.3对数运算(精讲)(原卷版+解析)，共19页。试卷主要包含了对数的定义，指对数的互化，对数求值，对数的运算等内容，欢迎下载使用。

考点一 对数的定义
【例1】1（2021·江西省吉水中学高一阶段练习）使式子有意义的x的取值范围是（ ）
A．B．C．D．
【一隅三反】
1．（2021·全国·高一课时练习）使有意义的实数a的取值范围是（ ）
A．B．
C．D．
2．（2022广东）对数式M＝lg(a－3)(10－2a)中，实数a的取值范围是（ ）
A．(－∞，5)B．(3，5)
C．(3，＋∞)D．(3，4)∪(4，5)
3．（2022·云南）在等式中，实数a的取值范围是（ ）
A．或B．或
C．D．
考点二 指对数的互化
【例2】（2022山西）将下列指数式与对数式互化：
(1)； (2)； (3)； (4)；(5)；(6)．
【一隅三反】
1.（2021·全国高一课时练习）指数式和对数式互相转化：
（1）____________．（2）____________．
（3）____________．（4）____________．
2．（2022·湖南）将下列指数式化为对数式，对数式化为指数式：
(1)；(2)；(3)；(4)．
考点三 对数求值
【例3】（2022·湖南·高一课时练习）求下列各式中的值：
(1)；(2)；(3)；(4)．
【一隅三反】
1．（2021·全国·高一课前预习）求下列各式中的值：
(1)；(2)；(3)；(4).
2．（2021·江苏·高一课时练习）求下列各式中x的值：
（1）lgx3＝；（2）lg64x＝－；（3）－lne2＝x；（4）；（5）lg5[lg3(lg2x)]＝0.
考点四 对数的运算
【例4】（2022北京）求值：
(1)；
(2)；
(3)；
(4).
(5)2lg32－lg3＋lg38－；
(6)(lg2125＋lg425＋lg85)·(lg52＋lg254＋lg1258).
(7)lg25＋lg2＋lg＋lg(0.01)－1；
(8)(lg2)2＋lg2·lg50＋lg25；
(9)(lg32＋lg92)·(lg43＋lg83)；
(10)2lg32－lg3＋lg38－3lg55；
【一隅三反】
1．（2022·全国·高三专题练习）化简下列各式：
（1）lg25＋lg2＋lg＋lg(0.01)－1；
（2）(lg2)2＋lg2·lg50＋lg25；
（3）计算(lg32＋lg92)·(lg43＋lg83)；
（4）2lg32－lg3＋lg38－3lg55；
2．（2021·全国·高一课时练习）计算下列各式：
（1）lg25＋lg2＋lg＋lg(0.01)－1；
（2）2lg32－lg3＋lg38－3lg55；
（3）(lg5)2＋lg2·lg50；
考点五 换底公式
【例5-1】（2022·全国·高一）（1）已知，，试用表示；
（2）已知，，试用表示．
【例5-2】（2021·全国·高一单元测试）已知，求证：.
【一隅三反】
1．（2022·全国·高一课时练习）已知，，则（ ）
A．B．
C．D．
2．（2022·湖南·高一课时练习）已知，求的值．
3．（2021·江苏·高一单元测试）已知a，b，c均为正数，且，求证：；
4.3 对数运算（精讲）
考点一 对数的定义
【例1】1（2021·江西省吉水中学高一阶段练习）使式子有意义的x的取值范围是（ ）
A．B．C．D．
【答案】D
【解析】要使式子有意义，则，即，解得或，
所以x的取值范围是.故选：D
【一隅三反】
1．（2021·全国·高一课时练习）使有意义的实数a的取值范围是（ ）
A．B．
C．D．
【答案】C
【解析】由题意知，解得，所以实数a的取值范围是．故选：C.
2．（2022广东）对数式M＝lg(a－3)(10－2a)中，实数a的取值范围是（ ）
A．(－∞，5)B．(3，5)
C．(3，＋∞)D．(3，4)∪(4，5)
【答案】D
【解析】由题意得，解得33．（2022·云南）在等式中，实数a的取值范围是（ ）
A．或B．或
C．D．
【答案】B
【解析】要使有意义，只需：，解得：或
∴实数a的取值范围是或故选：B
考点二 指对数的互化
【例2】（2022山西）将下列指数式与对数式互化：
(1)； (2)； (3)； (4)；(5)；(6)．
【答案】(1)；(2)；(3)；(4)；(5)；(6)．
【解析】(1)因为，所以有：.
(2)因为，所以有：.
(3)因为，所以有：.
(4)因为，所以有：.
(5)因为，所以有：.
(6)因为，所以有：.
【一隅三反】
1.（2021·全国高一课时练习）指数式和对数式互相转化：
（1）____________．（2）____________．
（3）____________．（4）____________．
【答案】
【解析】.故答案为：，，，.
2．（2022·湖南）将下列指数式化为对数式，对数式化为指数式：
(1)；(2)；(3)；(4)．
【答案】(1)(2)(3)(4)
【解析】(1)由对数定义得；
(2)由对数定义得；
(3)由对数定义得；
(4)由对数定义得．
考点三 对数求值
【例3】（2022·湖南·高一课时练习）求下列各式中的值：
(1)；(2)；(3)；(4)．
【答案】(1)125(2)(3)(4)
【解析】(1)因为，所以；
(2)因为，所以，解得
(3)因为，所以，所以；
(4)因为，所以，所以.
【一隅三反】
1．（2021·全国·高一课前预习）求下列各式中的值：
(1)；(2)；(3)；(4).
【答案】(1)；(2)；(3)；(4).
【解析】(1)由题意，.
(2)由题意，，而且，所以.
(3)由题意，.
(4)由题意，.
2．（2021·江苏·高一课时练习）求下列各式中x的值：
（1）lgx3＝；（2）lg64x＝－；（3）－lne2＝x；（4）；（5）lg5[lg3(lg2x)]＝0.
【答案】（1）9；（2）；（3）－2；（4）3；（5）8.
【解析】（1）由lgx3＝，得＝3，所以x＝9.
（2）由lg64x＝－，得x＝＝＝4－2＝，所以x＝.
（3）因为－lne2＝x，所以lne2＝－x，e2＝e－x，于是x＝－2.
（4）由，得2x2－4x＋1＝x2－2，
解得x＝1或x＝3，又因为x＝1时，x2－2＝－1<0，舍去；
x＝3时，x2－2＝7>0，2x2－4x＋1＝7>0，符合题意．综上，x＝3.
（5）由lg5[lg3(lg2x)]＝0，得lg3(lg2x)＝1，所以lg2x＝3，故x＝23，即x＝8.
考点四 对数的运算
【例4】（2022北京）求值：
(1)；
(2)；
(3)；
(4).
(5)2lg32－lg3＋lg38－；
(6)(lg2125＋lg425＋lg85)·(lg52＋lg254＋lg1258).
(7)lg25＋lg2＋lg＋lg(0.01)－1；
(8)(lg2)2＋lg2·lg50＋lg25；
(9)(lg32＋lg92)·(lg43＋lg83)；
(10)2lg32－lg3＋lg38－3lg55；
【答案】(1)(2)-1(3)1(4)2(5)－1(6)13(7)(8)2(9)(10)－1
【解析】(1)原式.
(2)
(3)原式=.
(4)原式==.
(5)原式＝2lg32－5lg32＋2＋3lg32－3＝－1.
(6)原式
.
(7)原式＝
(8)原式＝(lg2)2＋(1＋lg5)lg2＋lg52＝(lg2＋lg5＋1)lg2＋2lg5＝(1＋1)lg2＋2lg5＝2(lg2＋lg5)＝2.
(9)(lg32＋lg92)·(lg43＋lg83)＝·＝·
＝·＝.
(10)2lg32－lg3＋lg38－3lg55＝lg322＋lg3(32×2－5)＋lg323－3＝lg3(22×32×2－5×23)－3
＝lg332－3＝2－3＝－1.
【一隅三反】
1．（2022·全国·高三专题练习）化简下列各式：
（1）lg25＋lg2＋lg＋lg(0.01)－1；
（2）(lg2)2＋lg2·lg50＋lg25；
（3）计算(lg32＋lg92)·(lg43＋lg83)；
（4）2lg32－lg3＋lg38－3lg55；
【答案】（1）；（2）2；（3）；（4）－1.
【解析】（1）原式＝
（2）原式＝(lg2)2＋(1＋lg5)lg2＋lg52＝(lg2＋lg5＋1)lg2＋2lg5
＝(1＋1)lg2＋2lg5
＝2(lg2＋lg5)
＝2.
（3）(lg32＋lg92)·(lg43＋lg83)
＝·
＝·
＝·
＝.
（4）2lg32－lg3＋lg38－3lg55
＝lg322＋lg3(32×2－5)＋lg323－3
＝lg3(22×32×2－5×23)－3
＝lg332－3
＝2－3
＝－1.
2．（2021·全国·高一课时练习）计算下列各式：
（1）lg25＋lg2＋lg＋lg(0.01)－1；
（2）2lg32－lg3＋lg38－3lg55；
（3）(lg5)2＋lg2·lg50；
【答案】（1）；（2）；（3）1
【解析】（1）lg25＋lg2＋lg＋lg(0.01)－1
=
（2）2lg32－lg3＋lg38－3lg55
（3）(lg5)2＋lg2·lg50
(lg5)2
考点五 换底公式
【例5-1】（2022·全国·高一）（1）已知，，试用表示；
（2）已知，，试用表示．
【答案】（1）；（2）.
【解析】（1），，
，，
；
（2），，
．
【例5-2】（2021·全国·高一单元测试）已知，求证：.
【答案】证明见解析；
【解析】令，
则，，，
所以.
【一隅三反】
1．（2022·全国·高一课时练习）已知，，则（ ）
A．B．
C．D．
【答案】D
【解析】因为，，所以
．
故选：D.
2．（2022·湖南·高一课时练习）已知，求的值．
【答案】-1
【解析】由可得： ，
故
.
3．（2021·江苏·高一单元测试）已知a，b，c均为正数，且，求证：；
【答案】证明见解析
【解析】设，则.
∴，
∴，
而，
∴，得证.