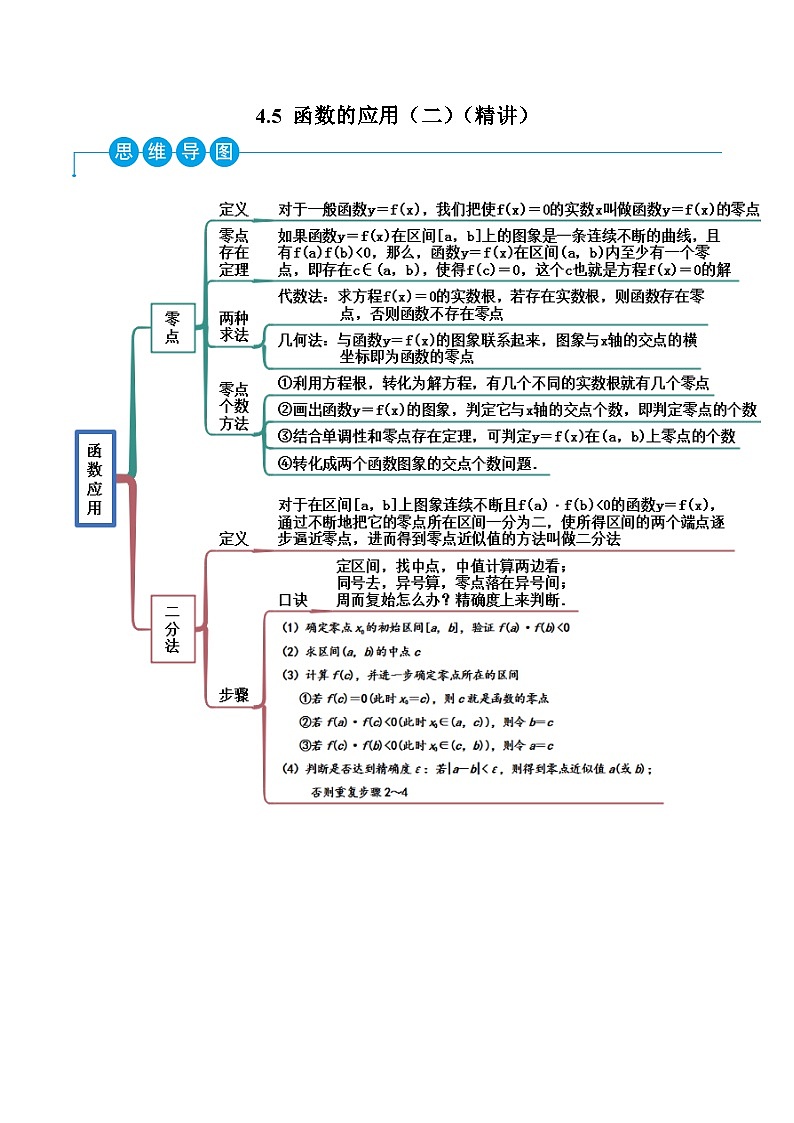

高一数学一隅三反系列(人教A版必修第一册)4.5函数的应用(二)(精讲)(原卷版+解析)
展开考点一 求零点
【例1】(2022·全国·高一单元测试)函数的零点为( )
A.10B.9
C.(10,0)D.(9,0)
【一隅三反】
1.(2022·全国·高一单元测试)若是函数的一个零点,则的另一个零点为( )
A.1B.2
C.(1,0)D.(2,0)
2.(2022·全国·高一课时练习)函数f(x)=x2﹣4x+4的零点是( )
A.(0,2)B.(2,0)
C.2D.4
3.(2021·全国·高一课时练习)函数的零点为________.
考点二 零点区间
【例2】(2022·山西·长治市第四中学校高一期末)函数的零点所在区间为( )
B.
C.D.
【一隅三反】
1.(2022·重庆·巫山县官渡中学高一期末)在下列区间中,函数的一个零点所在的区间为( ).
A.B.
C.D.
2.(2022·全国·高一)函数的零点所在的区间是( )
A.B.
C.D.
3.(2022·江苏扬州·高一期中)函数的零点所在的区间为( )
A.B.
C.D.
考点三 零点个数
【例3-1】(2022·广东茂名·高一期中)函数的零点的个数为( )
A.0B.1
C.2D.3
【例3-2】(2021·云南德宏·高一期末)若偶函数在定义域内满足,且当时,;则的零点的个数为( )
A.1B.2
C.9D.18
【一隅三反】
1.(2022·江苏·高一期中)函数的零点个数为( )
A.1B.2
C.3D.4
2.(2022·湖南·岳阳市第四中学高一阶段练习)函数的零点个数为( )
A.0B.1
C.2D.3
3.(2022·重庆·三模)已知函数,则函数的零点个数为( )
A.个B.个
C.个D.个
考点四 求参数
【例4-1】(2022·全国·益阳平高学校高一期末)已知函数若关于x的方程恰有三个不相等的实数解,则m的取值范围是( )
A.B.
C.D.
【例4-2】(2022·全国·高一单元测试)已知函数,,的零点分别为,,,以下说法正确的是( )
B.
C.D.
【一隅三反】
1.(2022·全国·高一课时练习)(多选)函数的一个零点在区间内,则实数a的可能取值是( )
A.0B.1
C.2D.3
2.(2021·湖北黄石·高一期中)(多选)已知函数,,若方程有两个不相等的实根,则实数的取值可以是( )
A.B.
C.D.
3.(2022·江苏省如皋中学高一期末)设为实数,函数在上有零点,则实数的取值范围为________.
4.5 函数的应用(二)(精讲)
考点一 求零点
【例1】(2022·全国·高一单元测试)函数的零点为( )
A.10B.9C.(10,0)D.(9,0)
【答案】A
【解析】令,即,所以,因此x=10,所以函数的零点为10,故选:A.
【一隅三反】
1.(2022·全国·高一单元测试)若是函数的一个零点,则的另一个零点为( )
A.1B.2C.(1,0)D.(2,0)
【答案】A
【解析】因为是函数的一个零点,所以,解得.设另一个零点为,则,解得,所以的另一个零点为1.故选:A.
2.(2022·全国·高一课时练习)函数f(x)=x2﹣4x+4的零点是( )
A.(0,2)B.(2,0)C.2D.4
【答案】C
【解析】由f(x)=x2﹣4x+4=0得,x=2,所以函数f(x)=x2﹣4x+4的零点是2,故选:C.
3.(2021·全国·高一课时练习)函数的零点为________.
【答案】
【解析】当时,令,解得;当时,令,解得(舍去),
所以函数存在零点,且零点为.故答案为:1.
考点二 零点区间
【例2】(2022·山西·长治市第四中学校高一期末)函数的零点所在区间为( )
A.B.C.D.
【答案】C
【解析】因为与在定义域上单调递增,
所以在定义域上单调递增,
又,,,
即,所以的零点位于内;故选:C
【一隅三反】
1.(2022·重庆·巫山县官渡中学高一期末)在下列区间中,函数的一个零点所在的区间为( ).
A.B.C.D.
【答案】B
【解析】由题意,函数,
可得,所以,
结合零点的存在定理,可得函数的一个零点所在的区间为.
故选:B.
2.(2022·全国·高一)函数的零点所在的区间是( )
A.B.C.D.
【答案】C
【解析】因为函数在上单调递增,在上单调递增,
所以在上单调递增.
当时,,
,,
.
由零点存在定理可得:函数的零点所在的区间是.
故选:C
3.(2022·江苏扬州·高一期中)函数的零点所在的区间为( )
A.B.C.D.
【答案】B
【解析】函数,是单调递增函数,
当 时,, ,故
故函数的零点所在的区间为,故选:B
考点三 零点个数
【例3-1】(2022·广东茂名·高一期中)函数的零点的个数为( )
A.0B.1C.2D.3
【答案】B
【解析】由于函数在上是增函数,且,
故函数在上有唯一零点,也即在上有唯一零点.故选:B.
【例3-2】(2021·云南德宏·高一期末)若偶函数在定义域内满足,且当时,;则的零点的个数为( )
A.1B.2C.9D.18
【答案】D
【解析】由可知偶函数周期为2,故先画出时,的函数图象,再分别利用偶函数关于轴对称、周期为2画出的函数图象,则的零点个数即为的零点个数,即的交点个数,易得在上有个交点,故在定义域内有18个交点.
故选:D
【一隅三反】
1.(2022·江苏·高一期中)函数的零点个数为( )
A.1B.2C.3D.4
【答案】C
【解析】令,可得,
则原命题即求与图象交点的个数,
分别作出与图象,如下所示
由图象可得,交点为A、B、C三点,
所以函数的零点个数为3.故选:C
2.(2022·湖南·岳阳市第四中学高一阶段练习)函数的零点个数为( )
A.0B.1C.2D.3
【答案】B
【解析】由,得,
令,
两函数图象如图所示,
因为两图象只有一个交点,所以方程只有一个根,
所以函数只有一个零点,
故选:B
3.(2022·重庆·三模)已知函数,则函数的零点个数为( )
A.个B.个C.个D.个
【答案】C
【解析】当时,由可得,解得(舍去);
当时,由可得,即或,解得或.
综上所述,函数的零点个数为.故选:C.
考点四 求参数
【例4-1】(2022·全国·益阳平高学校高一期末)已知函数若关于x的方程恰有三个不相等的实数解,则m的取值范围是( )
A.B.
C.D.
【答案】D
【解析】函数的图像如下图所示:
若关于x的方程恰有三个不相等的实数解,
则函数的图像与直线有三个交点,
若直线经过原点时,m=0,
若直线与函数的图像相切,令,令.
故.
故选:D.
【例4-2】(2022·全国·高一单元测试)已知函数,,的零点分别为,,,以下说法正确的是( )
A.B.C.D.
【答案】A
【解析】由题设,,,,
所以问题可转化为直线与,,
的图象的交点问题,函数图象如下.
由图知.故选:A.
【一隅三反】
1.(2022·全国·高一课时练习)(多选)函数的一个零点在区间内,则实数a的可能取值是( )
A.0B.1C.2D.3
【答案】BC
【解析】因为函数在定义域上单调递增,
所以函数在上单调递增,
由函数的一个零点在区间内,
得,解得,故选:BC
2.(2021·湖北黄石·高一期中)(多选)已知函数,,若方程有两个不相等的实根,则实数的取值可以是( )
A.B.C.D.
【答案】BC
【解析】因为,因为方程有两个不相等的实根,
则方程在和时各有一个实根,则,
当时,由得,可得;
当时,由可得,可得.
由题意可得,解得,
故选:BC.
3.(2022·江苏省如皋中学高一期末)设为实数,函数在上有零点,则实数的取值范围为________.
【答案】
【解析】因为在单调递增,且有零点,
所以,解得,
故答案为:.
高一数学一隅三反系列(人教A版必修第一册)4.3对数运算(精讲)(原卷版+解析): 这是一份高一数学一隅三反系列(人教A版必修第一册)4.3对数运算(精讲)(原卷版+解析),共19页。试卷主要包含了对数的定义,指对数的互化,对数求值,对数的运算等内容,欢迎下载使用。
高一数学一隅三反系列(人教A版必修第一册)4.1指数运算(精讲)(原卷版+解析): 这是一份高一数学一隅三反系列(人教A版必修第一册)4.1指数运算(精讲)(原卷版+解析),共15页。试卷主要包含了根式意义求参,根式化简,根式与分数指数幂互化,指数运算的综合运用等内容,欢迎下载使用。
高一数学一隅三反系列(人教A版必修第一册)3.4函数的应用(一)(精讲)(原卷版+解析): 这是一份高一数学一隅三反系列(人教A版必修第一册)3.4函数的应用(一)(精讲)(原卷版+解析),共20页。试卷主要包含了一次函数模型,二次函数模型,分段函数,基本不等式模型等内容,欢迎下载使用。












