高一数学一隅三反系列(人教A版必修第一册)5.1任意角与弧度制(精讲)(原卷版+解析)

这是一份高一数学一隅三反系列(人教A版必修第一册)5.1任意角与弧度制(精讲)(原卷版+解析)，共20页。试卷主要包含了角度制与弧度制的互换，终边相同的角，角象限的判断，概念的辨析，扇形的弧长与面积，实际应用等内容，欢迎下载使用。


考点一 角度制与弧度制的互换
【例1】（2022广东）把下列各角的弧度数化为度数，度数化为弧度数.
（1） ； （2） ； （3）1125° ； （4）-225°.
【一隅三反】
1．（2022宿州）将210°化成弧度为（ ）
A．B．C．D．
2．（2022房山期中）将120°转化为弧度为（ ）
A．B．C．D．
3．（2022山西月考）角度化成弧度为（ ）
A．B．C．D．
考点二 终边相同的角
【例2】（2022·涟水）在与 角终边相同的角中，求满足下列条件的角．
（1）最大的负角；
（2）最小的正角；
（3）在 内的角．
【一隅三反】
1．（2022陕西期末）在0~360°的范围内，下列与-510°终边相同的角是（ ）
A．330°B．210°C．150°D．30°
2（2022房山月考）在，，，中，与终边相同的是（ ）
A．B．C．D．
3．（2022海东）下列各组角中，终边相同的是（ ）
A．43°和313°B．37°和787°
C．65°和-655°D．124°和-576°
4（20222怀化）（多选）与角 终边相同的角是（ ）
A．B．C．D．
考点三 角象限的判断
【例3-1】（2022南阳）已知角，则角的终边落在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【例3-2】（2022砀山月考）角 的终边所在的象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【一隅三反】
1．（2022高一下·新余期末）410°角的终边落在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
2．（2022·河池月考）已知角，则角是（ ）
A．第一象限角B．第二象限角C．第三象限角D．第四象限角
3．（2022云南）角的终边所在的象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
考点四 概念的辨析
【例4】（2022山东）下列命题：①钝角是第二象限的角；②小于90º的角是锐角；③第一象限的角一定不是负角；④第二象限的角一定大于第一象限的角；⑤手表时针走过2小时，时针转过的角度为60º；⑥若，则是第四象限角．其中正确的题的个数是（ ）
A．1个B．2个C．3个D．4个
【一隅三反】
1．（2021·安徽蚌埠二中高一期中）下列说法中，正确的是（ ）
A．锐角是第一象限的角B．终边相同的角必相等
C．小于的角一定为锐角D．第二象限的角必大于第一象限的角
2．（2022·浙江）下列命题中正确的是（ ）．
A．终边与始边重合的角是零角B．90°～180°间的角不一定是钝角
C．终边和始边都相同的两个角相等D．第二象限的角大于第一象限的角
3．（2022·陕西大荔）下列说法正确的是（ ）
A．第二象限角大于第一象限角B．不相等的角终边可以相同
C．若是第二象限角，一定是第四象限角D．终边在轴正半轴上的角是零角
考点五 扇形的弧长与面积
【例5】已知扇形的圆心角是α，半径为R，弧长为l．
（1）若α=60°，R=10cm，求扇形的弧长l；
（2）若扇形的周长为20cm，当扇形的圆心角α为多少弧度时，这个扇形的面积最大；
（3）若α= ，R=2cm，求扇形的弧所在的弓形的面积．
【一隅三反】
1．（2022滨州期末）若扇形的周长为，面积为，则其圆心角的弧度数是（ ）
A．1或4B．1或2C．2或4D．1或5
2．（2022高一下·常州期中）已知扇形的周长为30cm，圆心角为3rad，则此扇形的弧长为（ ）
A．6cmB．12cmC．18cmD．24cm
3.（1）已知扇形的周长为10，面积为4，求扇形中心角的弧度数；
（2）已知扇形的周长为40，当它的半径和中心角取何值时，才能使扇形的面积最大？最大面积是多少？
考点六 实际应用
【例6】（2022定州）（多选）钟表在我们的生活中随处可见，高一某班的同学们在学习了“任意角和弧度制”后，对钟表的运行产生了浓厚的兴趣，并展开了激烈的讨论，若将时针与分针视为两条线段，则下列说法正确的是（ ）
A．小赵同学说：“经过了5 h，时针转了．”
B．小钱同学说：“经过了40 min，分针转了．”
C．小孙同学说：“当时钟显示的时刻为12：35时，时针与分针所夹的钝角为．”
D．小李同学说：“时钟的时针与分针一天之内会重合22次．”
【一隅三反】
1．（2022·兰溪期中）如图所示，一圆形钟的时针长 ，2021年11月9日上午 至 ，时针的针头自点 处转动到点 处，则线段 的长为 .
2．（2021杭州期中）《九章算术》是我国古代内容极为丰富的数学名著，其中有这样一个问题：“今有宛田，下周三十步，径十六步.问为田几何？”其意思为：“有一块扇形的田，弧长为30步，其所在圆的直径为16步，问这块田的面积是多少平方步？”该问题的答案为 平方步.
3．（2022如皋）达·芬奇的经典之作《蒙娜丽莎》举世闻名.如图，画中女子神秘的微笑，数百年来让无数观赏者人迷.某业余爱好者对《蒙娜丽莎》的缩小影像作品进行了粗略测绘，将画中女子的嘴唇近似看作一个圆弧，在嘴角处作圆弧的切线，两条切线交于B点，测得如下数据：（其中）.根据测量得到的结果推算：将《蒙娜丽莎》中女子的嘴唇视作的圆弧对应的圆心角大约等于（ ）
A．B．C．D．
4．（202临潼期末）中国传统扇文化有着极其深厚的底蕴．一般情况下，折扇可看作是从一个圆面中剪下的扇形制作而成，设扇形的面积为S1 ，圆面中剩余部分的面积为，当S1与的比值为 时，扇面看上去形状较为美观，那么此时扇形的圆心角的弧度数为（ ）
A．B．C．D．
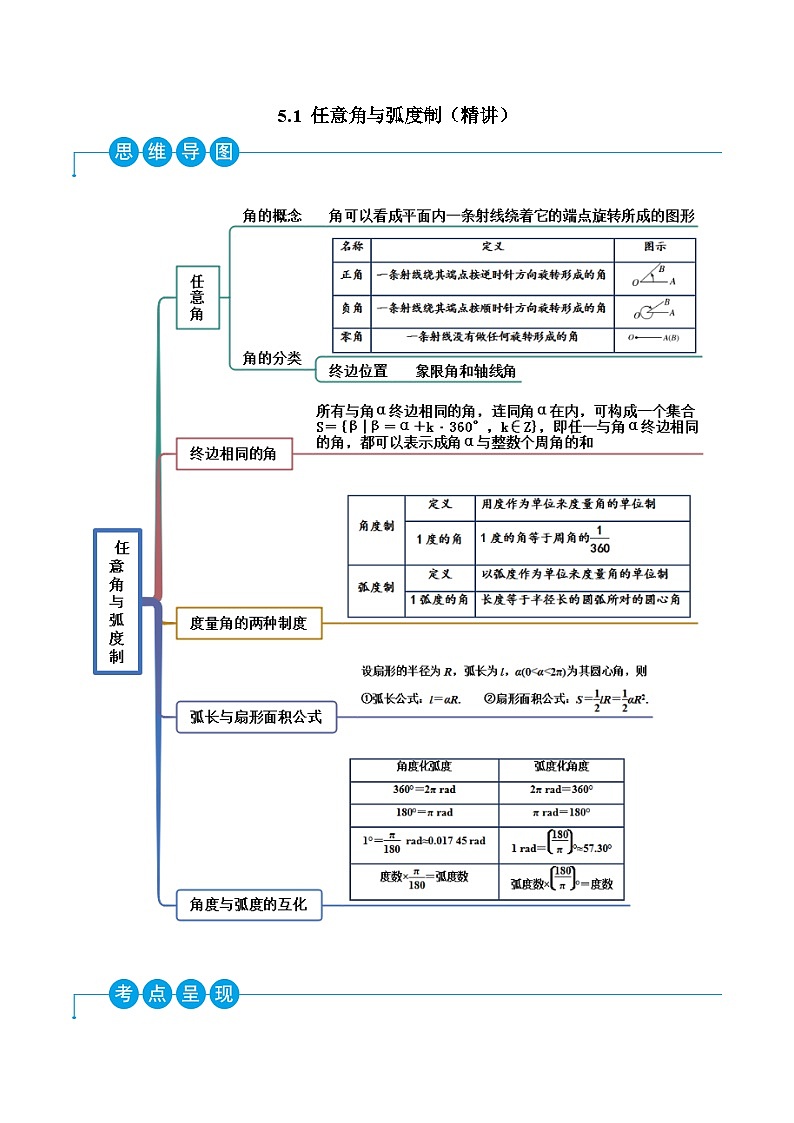
5.1 任意角与弧度制（精讲）
考点一 角度制与弧度制的互换
【例1】（2022广东）把下列各角的弧度数化为度数，度数化为弧度数.
（1） ； （2） ； （3）1125° ； （4）-225°.
【答案】（1）105° （2）-390° （3）254π （4）- 54π
【解析】（1）根据弧度制与角度制的互化公式， ，可得：
；
（2）
（3） ；
（4） .
【一隅三反】
1．（2022宿州）将210°化成弧度为（ ）
A．B．C．D．
【答案】D
【解析】。 故答案为：D.
2．（2022房山期中）将120°转化为弧度为（ ）
A．B．C．D．
【答案】B
【解析】， 故答案为：B.
3．（2022山西月考）角度化成弧度为（ ）
A．B．C．D．
【答案】A
【解析】根据题意，。 故答案为：A.
考点二 终边相同的角
【例2】（2022·涟水）在与 角终边相同的角中，求满足下列条件的角．
（1）最大的负角；
（2）最小的正角；
（3）在 内的角．
【答案】见解析
【解析】（1）解：与 角终边相同的角为 ， .
由 且 ，可得 ，故所求的最大负角为
（2）解：由 且 ，可得 ，故所求的最小正角为
（3）解：由 且 ，可得 ，故所求的角为
【一隅三反】
1．（2022陕西期末）在0~360°的范围内，下列与-510°终边相同的角是（ ）
A．330°B．210°C．150°D．30°
【答案】B
【解析】因为-510°=-720°+210°，则在0°~360°的范围内，与-510°终边相同的角是210° .故选：B
2（2022房山月考）在，，，中，与终边相同的是（ ）
A．B．C．D．
【答案】D
【解析】与终边相同的角为：； 当时，.故答案为：D.
3．（2022海东）下列各组角中，终边相同的是（ ）
A．43°和313°B．37°和787°
C．65°和-655°D．124°和-576°
【答案】C
【解析】 . 故答案为：C．
4（20222怀化）（多选）与角 终边相同的角是（ ）
A．B．C．D．
【答案】BD
【解析】与角 终边相同的角的集合是 ，
当 时， ，当 时， .故答案为：BD
考点三 角象限的判断
【例3-1】（2022南阳）已知角，则角的终边落在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】C
【解析】因为，而是第三象限角，故角的终边落在第三象限.
故答案为：C.
【例3-2】（2022砀山月考）角 的终边所在的象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】C
【解析】 ，则与 终边相同，故角 的终边所在的象限是
第三象限.故答案为：C
【一隅三反】
1．（2022高一下·新余期末）410°角的终边落在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】A
【解析】，故为第一象限角。 故答案为：A．
2．（2022·河池月考）已知角，则角是（ ）
A．第一象限角B．第二象限角C．第三象限角D．第四象限角
【答案】C
【解析】因为所以与是同一象限角，
因为是第三象限角，故为第三象限角．故答案为：C．
3．（2022云南）角的终边所在的象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】D
【解析】因为，所以角与角是终边相同的角，
又，所以角的终边在第四象限.故选：D
考点四 概念的辨析
【例4】（2022山东）下列命题：①钝角是第二象限的角；②小于90º的角是锐角；③第一象限的角一定不是负角；④第二象限的角一定大于第一象限的角；⑤手表时针走过2小时，时针转过的角度为60º；⑥若，则是第四象限角．其中正确的题的个数是（ ）
A．1个B．2个C．3个D．4个
【答案】B
【解析】对于①：钝角是大于小于的角，显然钝角是第二象限角. 故①正确；
对于②：锐角是大于小于的角，小于的角也可能是负角. 故②错误；
对于③：显然是第一象限角. 故③错误；
对于④：是第二象限角，是第一象限角，但是. 故④错误；
对于⑤：时针转过的角是负角. 故⑤错误；
对于⑥：因为，所以，是第四象限角. 故⑥正确.
综上所述，①⑥正确.故答案为：B.
【一隅三反】
1．（2021·安徽蚌埠二中高一期中）下列说法中，正确的是（ ）
A．锐角是第一象限的角B．终边相同的角必相等
C．小于的角一定为锐角D．第二象限的角必大于第一象限的角
【答案】A
【解析】对于A中，根据锐角的定义，可得锐角满足是第一象限角，所以A正确；
对于B中，例如：与的终边相同，但，所以B不正确；
对于C中，例如：满足，但不是锐角，所以C不正确；
对于D中，例如：为第一象限角，为第二象限角，此时，所以D不正确.
故选：A.
2．（2022·浙江）下列命题中正确的是（ ）．
A．终边与始边重合的角是零角B．90°～180°间的角不一定是钝角
C．终边和始边都相同的两个角相等D．第二象限的角大于第一象限的角
【答案】B
【解析】终边与始边重合的角还有360°角，720°角等，故A错误；
90°～180°间的角包括90°角，故90°～180°间的角不一定是钝角，故B正确；
终边和始边都相同的两个角相差，故C错误；
120°角是第二象限角，它小于第一象限的角400°角，故D错误．故选：B
3．（2022·陕西大荔）下列说法正确的是（ ）
A．第二象限角大于第一象限角B．不相等的角终边可以相同
C．若是第二象限角，一定是第四象限角D．终边在轴正半轴上的角是零角
【答案】B
【解析】A选项，第一象限角，而是第二象限角，∴该选项错误；
B选项，与终边相等，但它们不相等，∴该选项正确；
C选项，若是第二象限角，则，
∴是第三象限角或第四象限角或终边在轴负半轴上的轴线角，∴该选项错误；D选项，角的终边在轴正半轴上，但不是零角，∴该选项错误.故选：.
考点五 扇形的弧长与面积
【例5】已知扇形的圆心角是α，半径为R，弧长为l．
（1）若α=60°，R=10cm，求扇形的弧长l；
（2）若扇形的周长为20cm，当扇形的圆心角α为多少弧度时，这个扇形的面积最大；
（3）若α= ，R=2cm，求扇形的弧所在的弓形的面积．
【答案】见解析
（1）解：l=10× = （cm）．
（2）解：由已知得：l+2R=20，
所以S= lR= （20﹣2R）R=﹣（R﹣5）2+25．
所以R=5时，S取得最大值25，此时l=10，α=2rad．
（3）解：设弓形面积为S弓，由题知l= cm， S弓=S扇﹣S△= ×22×sin （cm2）．
【一隅三反】
1．（2022滨州期末）若扇形的周长为，面积为，则其圆心角的弧度数是（ ）
A．1或4B．1或2C．2或4D．1或5
【答案】A
【解析】设扇形的半径为，弧长为，由题意得2R+l=1212Rl=8，解得l=4R=4或l=8R=2，
故扇形的圆心角的弧度数或 4．故答案为：A.
2．（2022高一下·常州期中）已知扇形的周长为30cm，圆心角为3rad，则此扇形的弧长为（ ）
A．6cmB．12cmC．18cmD．24cm
【答案】C
【解析】由题意得：扇形的半径为，圆心角为3rad
扇形的周长为：，解得
所以扇形的弧长为：故答案为：C
3.（1）已知扇形的周长为10，面积为4，求扇形中心角的弧度数；
（2）已知扇形的周长为40，当它的半径和中心角取何值时，才能使扇形的面积最大？最大面积是多少？
【答案】见解析
【解析】（1）解：设扇形的弧长为l，圆心角大小为α（rad），半径为r，
由题意可得：2r+l=10， ×l×r=4，
解得： ，或 ．
故扇形中心角的弧度数为 = ，或8（由于8＞2π，舍去）．
（2）解：设扇形的半径和弧长分别为r和l，
由题意可得2r+l=40，
∴扇形的面积S= lr= •l•2r≤ （ ）2=100，
当且仅当l=2r=20，即l=20，r=10时取等号，
此时圆心角为α= =2，
∴当半径为10圆心角为2时，扇形的面积最大，最大值为100．
考点六 实际应用
【例6】（2022定州）（多选）钟表在我们的生活中随处可见，高一某班的同学们在学习了“任意角和弧度制”后，对钟表的运行产生了浓厚的兴趣，并展开了激烈的讨论，若将时针与分针视为两条线段，则下列说法正确的是（ ）
A．小赵同学说：“经过了5 h，时针转了．”
B．小钱同学说：“经过了40 min，分针转了．”
C．小孙同学说：“当时钟显示的时刻为12：35时，时针与分针所夹的钝角为．”
D．小李同学说：“时钟的时针与分针一天之内会重合22次．”
【答案】ACD
【解析】经过了5 h，时针转过的角度对应的弧度数为，A符合题意．
经过了40 min，分针转过的角度对应的弧度数为，B不符合题意．
时钟显示的时刻为12：35，该时刻的时针与分针所夹的钝角为，C符合题意．
分针比时针多走一圈便会重合一次，设分针走了t min，第n次和时针重合，则，得，故，D符合题意．
故答案为：ACD
【一隅三反】
1．（2022·兰溪期中）如图所示，一圆形钟的时针长 ，2021年11月9日上午 至 ，时针的针头自点 处转动到点 处，则线段 的长为 .
【答案】
【解析】2021年11月9日上午7：00至11：00，时针的针头自点 处转动到点 处，
则时针转过的弧度数为 ，故 。
故答案为： 。
2．（2021杭州期中）《九章算术》是我国古代内容极为丰富的数学名著，其中有这样一个问题：“今有宛田，下周三十步，径十六步.问为田几何？”其意思为：“有一块扇形的田，弧长为30步，其所在圆的直径为16步，问这块田的面积是多少平方步？”该问题的答案为 平方步.
【答案】120
【解析】由题意得：扇形的弧长为30，半径为8，
所以扇形的面积为： ，所以这块田的面积为120平方步 。
故答案为：120。
3．（2022如皋）达·芬奇的经典之作《蒙娜丽莎》举世闻名.如图，画中女子神秘的微笑，数百年来让无数观赏者人迷.某业余爱好者对《蒙娜丽莎》的缩小影像作品进行了粗略测绘，将画中女子的嘴唇近似看作一个圆弧，在嘴角处作圆弧的切线，两条切线交于B点，测得如下数据：（其中）.根据测量得到的结果推算：将《蒙娜丽莎》中女子的嘴唇视作的圆弧对应的圆心角大约等于（ ）
A．B．C．D．
【答案】A
【解析】依题意，设． 则．，．
设《蒙娜丽莎》中女子的嘴唇视作的圆弧对应的圆心角为．则，．故答案为：A．
4．（202临潼期末）中国传统扇文化有着极其深厚的底蕴．一般情况下，折扇可看作是从一个圆面中剪下的扇形制作而成，设扇形的面积为S1 ，圆面中剩余部分的面积为，当S1与的比值为 时，扇面看上去形状较为美观，那么此时扇形的圆心角的弧度数为（ ）
A．B．C．D．
【答案】A
【解析】S1与所在扇形圆心角的比即为它们的面积比，
设S1与所在扇形圆心角分别为，
则 ，又，解得故答案为：A