高一数学一隅三反系列(人教A版必修第一册)5.5三角恒等变换(精讲)(原卷版+解析)

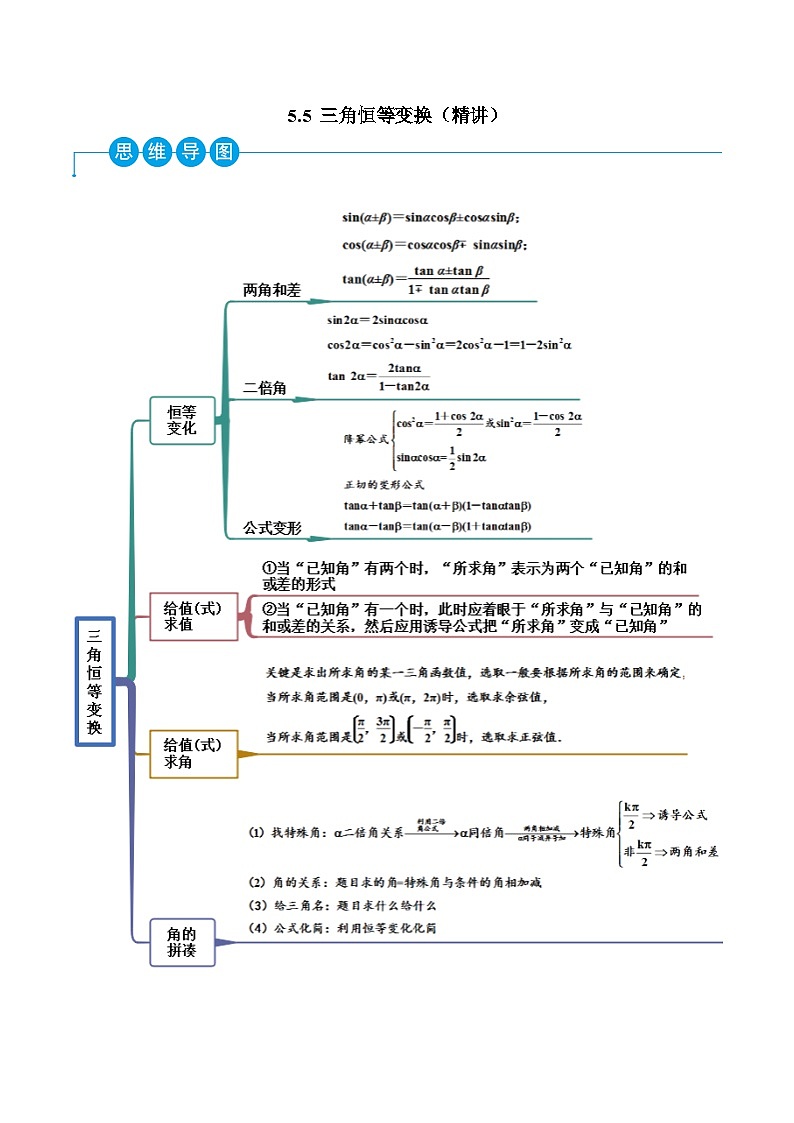
这是一份高一数学一隅三反系列(人教A版必修第一册)5.5三角恒等变换(精讲)(原卷版+解析)，共22页。试卷主要包含了两角和差与二倍角公式，给值求值，给值求角，辅助角公式，恒等变化等内容，欢迎下载使用。

考点一 两角和差与二倍角公式
【例1-1】（2022湖北）（ ）
A．B．C．D．1
【例1-2】（2022湖北月考）（ ）
A．1B．-1C．D．
【例1-3】（2022高一下·开封期末）已知角为第二象限角，，则的值为（ ）
A．B．C．D．
【例1-4】（2022高一下·湛江期末）（多选）下列各式中，值为的是（ ）
A．B．
C．D．
【一隅三反】
1．（2022河南）（ ）
A．B．C．D．
2．（2022昌平期末）在平面直角坐标系中，角以为始边，终边经过点，则（ ）
A．B．C．1D．5
3（2022高一下·郫都期中）若，是方程两个实数根，则（ ）
A．B．C．D．
4（2022湖北）（多选）下列三角式中，值为1的是（ ）
A．B．
C．D．
考点二 给值求值
【例2-1】（2022日照）已知锐角满足，，则的值为（ ）
A．B．C．D．
【例2-2】（2022高一下·武汉期末）已知，则的值是（ ）
A．B．C．D．
【例2-3】（2022高一下·汕尾期末）已知，则的值是（ ）
A．B．C．D．
【一隅三反】
1．（2022高二下·甘孜期末）若 ， 则（ ）
A．B．C．D．
2．（2022高二下·南宁期末）已知，则（ ）
A．B．C．D．
3．（2022高一下·景德镇期末）若为关于x的方程的两个根，则的值为（ ）
A．B．C．D．
4．（2022高一下·新余期末）已知，则的值是（ ）
A．B．C．D．
5．（2022·广州模拟）已知，则（ ）
A．B．C．D．
6．（2022·济宁模拟）已知，则（ ）
A．B．C．D．
考点三 给值求角
【例3】（2021·全国）已知，求角的值．
【一隅三反】
1．（2022西安）已知，其中，求角的值.
2．（2022云南）已知，且，求角的值．
3．（2022·江苏）已知，均为锐角，且，．
（1）求的值；
（2）求的值．
考点四 辅助角公式
【例4】（2022中山）将下列函数化简成
（1）
（2）
（3）
【一隅三反】
（2022广东湛江）将下列函数化简成
（2）
（3）
（4）
（5）
考点五 恒等变化
【例5-1】（2022镇江）计算：（ ）
A．1B．2C．3D．4
【例5-2】（2022高一下·西昌期中）若，，则的大小关系是（ ）
A．B．C．D．
【一隅三反】
1．（2022高一下·镇江期末）计算：（ ）
A．1B．2C．3D．4
2．（2022·广东模拟）（ ）
A．2B．-2C．D．
3．（2022高一下·陕西期末） 的值是（ ）
A．2B．4C．8D．16
4．（2020高一上·迁安期末） 的值 .
5.5 三角恒等变换（精讲）
考点一 两角和差与二倍角公式
【例1-1】（2022湖北）（ ）
A．B．C．D．1
【答案】B
【解析】
.故答案为：B
【例1-2】（2022湖北月考）（ ）
A．1B．-1C．D．
【答案】B
【解析】，故
故答案为：B
【例1-3】（2022高一下·开封期末）已知角为第二象限角，，则的值为（ ）
A．B．C．D．
【答案】D
【解析】因为角为第二象限角，所以，
则。故答案为：D.
【例1-4】（2022高一下·湛江期末）（多选）下列各式中，值为的是（ ）
A．B．
C．D．
【答案】BC
【解析】对于A：，A不符合题意
对于B：，B符合题意
对于C：，C符合题意；
对于D：，D不符合题意；故答案为：BC
【一隅三反】
1．（2022河南）（ ）
A．B．C．D．
【答案】B
【解析】
，A，C，D不符合题意.
故答案为：B.
2．（2022昌平期末）在平面直角坐标系中，角以为始边，终边经过点，则（ ）
A．B．C．1D．5
【答案】A
【解析】因为角以为始边，终边经过点， 所以，
所以。故答案为：A.
3（2022高一下·郫都期中）若，是方程两个实数根，则（ ）
A．B．C．D．
【答案】A
【解析】由韦达定理得：，，
所以。故答案为：A
4（2022湖北）（多选）下列三角式中，值为1的是（ ）
A．B．
C．D．
【答案】ABC
【解析】A选项,，故正确.
B选项，，故正确.
C选项，，故正确.
D选项，，故错误故选：ABC
考点二 给值求值
【例2-1】（2022日照）已知锐角满足，，则的值为（ ）
A．B．C．D．
【答案】A
【解析】为锐角，，，
又，.
故答案为：A.
【例2-2】（2022高一下·武汉期末）已知，则的值是（ ）
A．B．C．D．
【答案】A
【解析】由已知，化简，
即，
即，平方可得：，解得：.故答案为：A.
【例2-3】（2022高一下·汕尾期末）已知，则的值是（ ）
A．B．C．D．
【答案】A
【解析】由得：
，所以，，
所以，。故答案为：A.
【一隅三反】
1．（2022高二下·甘孜期末）若 ， 则（ ）
A．B．C．D．
【答案】C
【解析】因为，
所以，。故答案为：C
2．（2022高二下·南宁期末）已知，则（ ）
A．B．C．D．
【答案】A
【解析】．
故答案为：A
3．（2022高一下·景德镇期末）若为关于x的方程的两个根，则的值为（ ）
A．B．C．D．
【答案】B
【解析】因为为关于x的方程的两个根，
所以，，
因为，所以，
所以，
所以，故答案为：B
4．（2022高一下·新余期末）已知，则的值是（ ）
A．B．C．D．
【答案】B
【解析】。 故答案为：B
5．（2022·广州模拟）已知，则（ ）
A．B．C．D．
【答案】A
【解析】，， .故答案为：A.
6．（2022·济宁模拟）已知，则（ ）
A．B．C．D．
【答案】D
【解析】.
故答案为：D.
考点三 给值求角
【例3】（2021·全国）已知，求角的值．
【答案】
【解析】因为，所以．又因为，所以．
因为，所以，
所以．
又因为，所以．
【一隅三反】
1．（2022西安）已知，其中，求角的值.
【答案】
【解析】因为，所以.
因为，所以.
由已知可得，，
则
.
因为，所以.
2．（2022云南）已知，且，求角的值．
【答案】
【解析】依题意，且，
所以.
所以
.
，两者相加得，
所以.
3．（2022·江苏）已知，均为锐角，且，．
（1）求的值；
（2）求的值．
【答案】（1）；（2）．
【解析】（1）由，则．
所以，．
（2）因为，为锐角，则，所以．
所以，．又，所以．
考点四 辅助角公式
【例4】（2022中山）将下列函数化简成
（1）
（2）
（3）
【答案】见解析
【解析】（1），
即
（2
（3）
【一隅三反】
（2022广东湛江）将下列函数化简成
（2）
（3）
（4）
（5）
【答案】见解析
【解析】（1）
考点五 恒等变化
【例5-1】（2022镇江）计算：（ ）
A．1B．2C．3D．4
【答案】C
【解析】，
故答案为：C
【例5-2】（2022高一下·西昌期中）若，，则的大小关系是（ ）
A．B．C．D．
【答案】D
【解析】由已知得
，
，
，
因为在上单调递增，
所以，
所以。
故答案为：D.
【一隅三反】
1．（2022高一下·镇江期末）计算：（ ）
A．1B．2C．3D．4
【答案】C
【解析】，
故答案为：C
2．（2022·广东模拟）（ ）
A．2B．-2C．D．
【答案】C
【解析】． 故答案为：C
3．（2022高一下·陕西期末） 的值是（ ）
A．2B．4C．8D．16
【答案】B
【解析】
=[(1+tan21°) (1+tan24°) ][(1+tan22°) (1+tan23°) ]
=(1+tan21°tan24°+tan21°+tan24°) (1+tan22°tan23°+tan22°+tan23°)
=[1+tan21°tan24°+tan45°(1-tan21°tan24°)][1+tan22°tan23°+tan45°(1-tan22°tan23°)]
=(1+1)(1+1)
=4
故选：B
4．（2020高一上·迁安期末） 的值 .
【答案】1
【解析】
。故答案为：1。