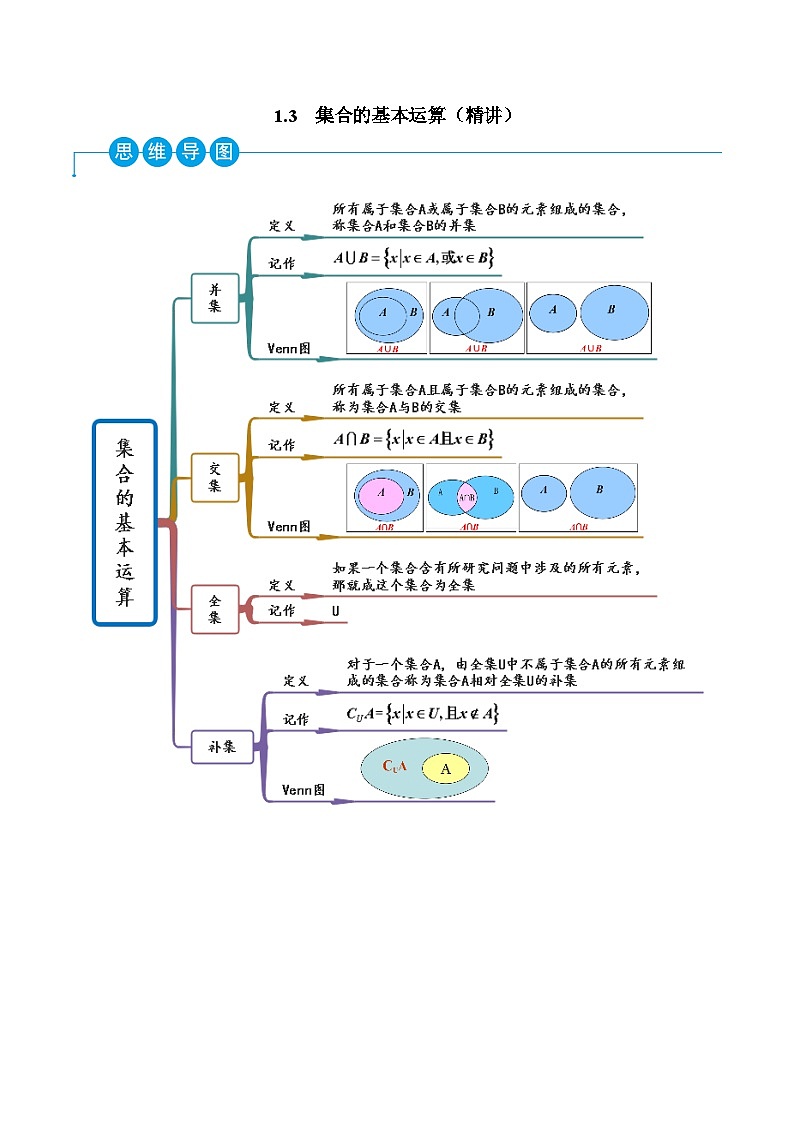
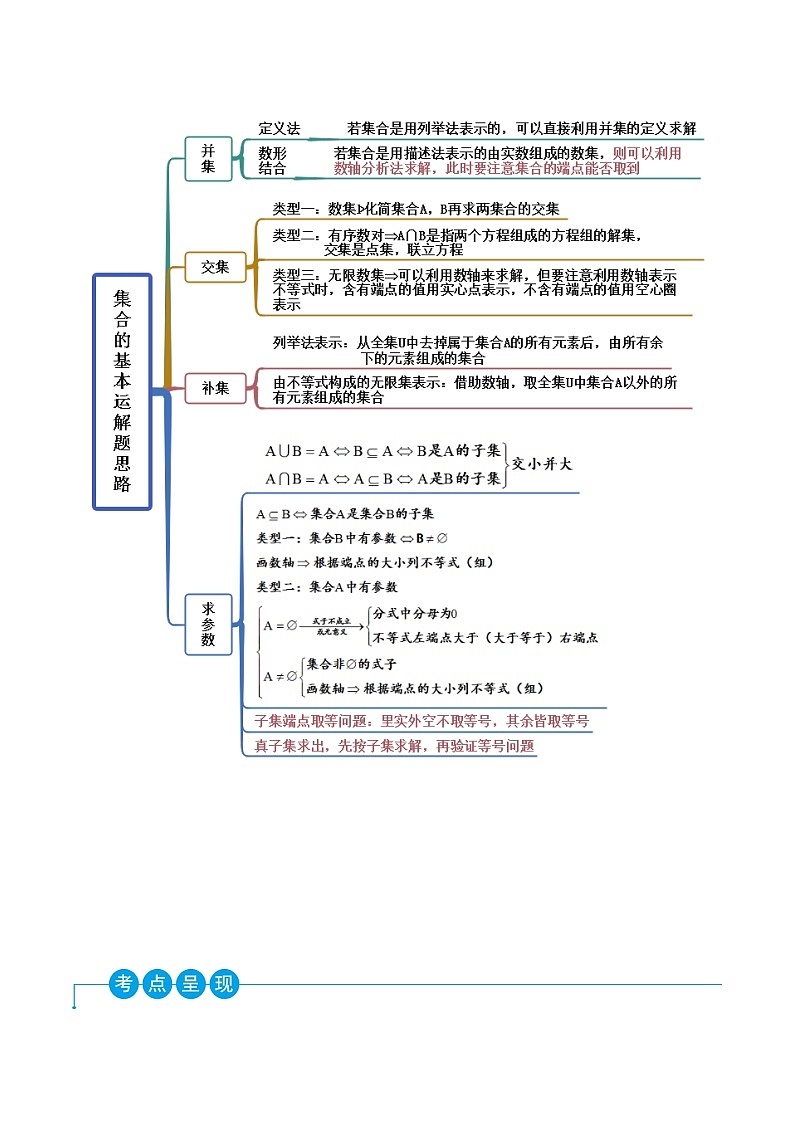
高一数学一隅三反系列(人教A版必修第一册)1.3集合的基本运算(精讲)(原卷版+解析)

这是一份高一数学一隅三反系列(人教A版必修第一册)1.3集合的基本运算(精讲)(原卷版+解析)，共23页。试卷主要包含了交集，并集，全集、补集，求参，韦恩图等内容，欢迎下载使用。


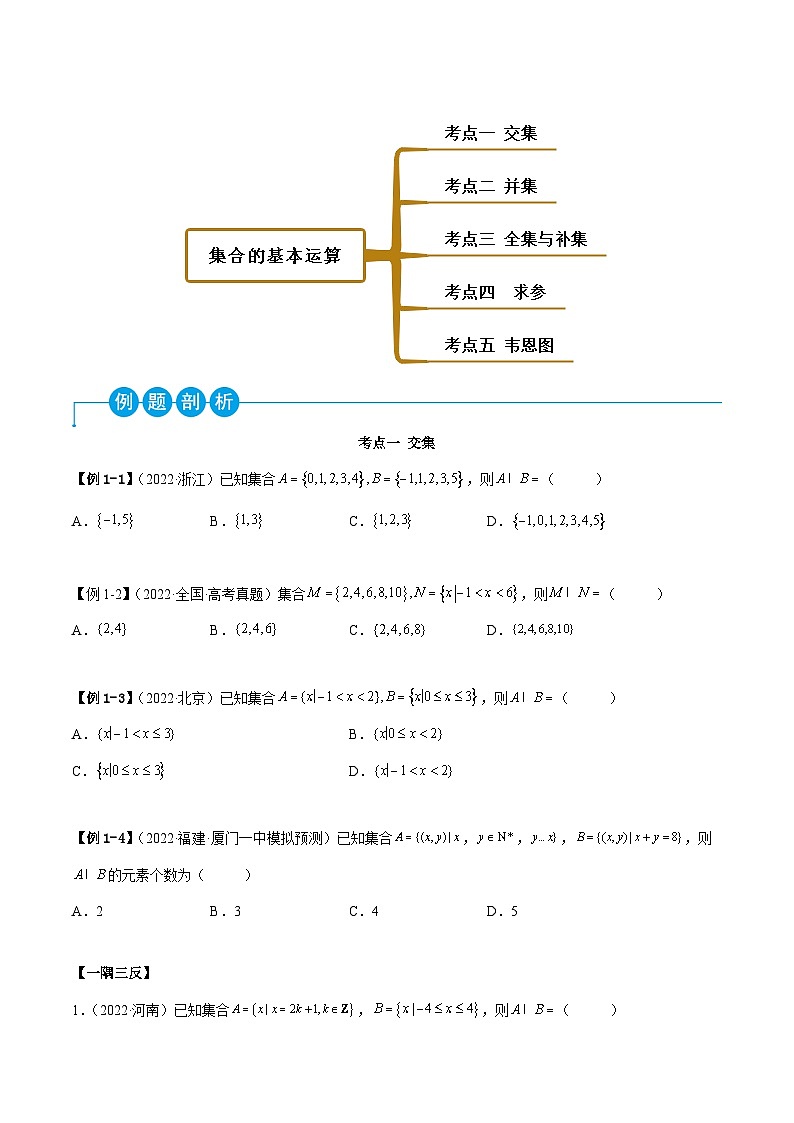
考点一 交集
【例1-1】（2022·浙江）已知集合，则（ ）
A．B．C．D．

【例1-2】（2022·全国·高考真题）集合，则（ ）
A．B．C．D．
【例1-3】（2022·北京）已知集合，则（ ）
A．B．
C．D．
【例1-4】（2022·福建·厦门一中模拟预测）已知集合，，，，则的元素个数为（ ）
A．2B．3C．4D．5
【一隅三反】
1．（2022·河南）已知集合，，则（ ）
A．B．C．D．
2．（2022·浙江·杭师大附中模拟预测）已知集合，则（ ）
A．B．
C． 或D．
3．（2022·青海玉树）设集合，则（ ）
A．B．C．D．
4．（2022·云南师大附中模拟预测（理））已知集合，，则集合的子集个数为（ ）
A．2B．4C．8D．16
考点二 并集
【例2-1】（2022·浙江·高考真题）设集合，则（ ）
A．B．C．D．
【例2-2】（2022·江苏省天一中学）已知集合，则（ ）
A．B．C．D．
【一隅三反】
1（2022·河北）已知集合，集合，则（ ）
B．C．D．
2（2022·宁夏）已知集合，，则等于（ ）
A．B．C．D．
3．（2022·河北·沧县中学模拟预测）若集合，则（ ）
A．B．
C．D．
考点三 全集、补集
【例3-1】（2022·北京·高考真题）已知全集，集合，则（ ）
A．B．C．D．
【例3-2】（2022·青海玉树）已知集合，则（ ）
A．B．C．D．
【例3-3】（2022·河北沧州）设集合P，Q均为全集U的非空子集，且，则（ ）
A．B．C．D．
【一隅三反】
1．（2022·北京八十中模拟预测）已知，，则___________.
2．（2022·全国·高三专题练习）已知全集，则（ ）
A．B．C．D．
3．（2022·全国·专题练习）（多选）已知全集U的两个非空真子集A，B满足，则下列关系一定正确的是（ ）
A．B．
C．D．
考点四 求参
【例4-1】（2022·湖南师大附中）已知集合，，若，则B=（ ）
A．B．C．D．
【例4-2】（2022·全国·高三专题练习（理））设，，若，则实数的值不可以是（ ）
A．0B．C．D．2
【例4-3】（2022·云南师大附中）已知集合，，且，则实数的所有值构成的集合是（ ）
A．B．C．D．
【例4-4】（2022·贵州毕节·高一期末）已知集合或，，若，则实数a的取值范围是（ ）
A．B．
C．D．
【例4-5】（2022·全国·池州市第一中学高一开学考试）已知集合，．
(1)当时，求；
(2)若______，求实数a的取值范围．
请从①，②，③，这三个条件中选一个填入（2）中横线顶处，并完成第（2）问的解答．（如果选择多个条件分别解答，按第一个解答计分）
【一隅三反】
1．（2022·陕西·西北工业大学附属中学模拟预测（理））已集合，集合，，则实数a的取值范围为（ ）
A．B．C．D．
2．（2022·广东·深圳实验学校高一期中）已知集合，，若满足，则的值为( )
A．或5B．或5C．D．5
3．（2022·全国·高三专题练习）已知集合，若，则x的不同取值个数为（ ）
A．1B．2C．3D．4
4．（2022·浙江）已知全集，集合.若，则（ ）
A．4B．3C．2D．0
5．（2022·江苏·扬州中学高一开学考试）已知集合.
(1)在①，②，③这三个条件中选择一个条件，求；
(2)若，求实数的取值范围.
6．（2022·云南玉溪·高一期末）已知集合，．
(1)若，求；
(2)在①，②，③，这三个条件中任选一个作为已知条件，求实数的取值范围．
考点五 韦恩图
【例5】（2022·江西萍乡）如图，全集，，，则阴影部分表示的集合为（ ）
A．B．C．D．
【一隅三反】
1．（2022·安徽合肥）设全集，集合，，则下面Venn图中阴影部分表示的集合是（ ）
A．B．
C．D．
2．（2022·全国·模拟预测）已知全集，，，则图中阴影部分表示的集合是（ ）
A．B．C．D．
3．（2022·全国·高三专题练习（文））设U＝R，已知两个非空集合P，Q满足＝R，则（ ）
A．P∩Q＝RB．PQ
C．QPD．P∪Q＝R
1.3 集合的基本运算（精讲）
考点一 交集
【例1-1】（2022·浙江）已知集合，则（ ）
A．B．C．D．
【答案】C
【解析】由题意中的条件有.故选：C
【例1-2】（2022·全国·高考真题）集合，则（ ）
A．B．C．D．
【答案】A
【解析】因为，，所以．故选：A.
【例1-3】（2022·北京）已知集合，则（ ）
A．B．
C．D．
【答案】B
【解析】依题意可知，解得，所以，故选：.
【例1-4】（2022·福建·厦门一中模拟预测）已知集合，，，，则的元素个数为（ ）
A．2B．3C．4D．5
【答案】C
【解析】集合,,，，
∴, ∴的元素个数为．故选：．
【一隅三反】
1．（2022·河南）已知集合，，则（ ）
A．B．C．D．
【答案】D
【解析】∵，，∴.故选：D.
2．（2022·浙江·杭师大附中模拟预测）已知集合，则（ ）
A．B．
C． 或D．
【答案】B
【解析】因为集合，所以，故选：B．
3．（2022·青海玉树）设集合，则（ ）
A．B．C．D．
【答案】B
【解析】因为是非零自然数集，所以故选：B
4．（2022·云南师大附中模拟预测（理））已知集合，，则集合的子集个数为（ ）
A．2B．4C．8D．16
【答案】B
【解析】由题意得，
当时， 联立，解得 ；当时， 联立，解得 ；
故抛物线与曲线有两个公共点，分别为，，
则集合有两个元素，所以的子集个数为，故选:B．
考点二 并集
【例2-1】（2022·浙江·高考真题）设集合，则（ ）
A．B．C．D．
【答案】D
【解析】，故选：D.
【例2-2】（2022·江苏省天一中学）已知集合，则（ ）
A．B．C．D．
【答案】B
【解析】，故选：B
【一隅三反】
1（2022·河北）已知集合，集合，则（ ）
A．B．C．D．
【答案】B
【解析】易知或，，故选：B
2（2022·宁夏）已知集合，，则等于（ ）
A．B．C．D．
【答案】B
【解析】因为，，所以；故选：B
3．（2022·河北·沧县中学模拟预测）若集合，则（ ）
A．B．
C．D．
【答案】D
【解析】由题意可知，又，所以．
故选：D．
考点三 全集、补集
【例3-1】（2022·北京·高考真题）已知全集，集合，则（ ）
A．B．C．D．
【答案】D
【解析】由补集定义可知：或，即，故选：D．
【例3-2】（2022·青海玉树）已知集合，则（ ）
A．B．C．D．
【答案】D
【解析】因，则，而，
所以.故选：D
【例3-3】（2022·河北沧州）设集合P，Q均为全集U的非空子集，且，则（ ）
A．B．C．D．
【答案】B
【解析】因为，所以，所以，所以；故选：B
【一隅三反】
1．（2022·北京八十中模拟预测）已知，，则___________.
【答案】
【解析】因为，，所以或；
故答案为：
2．（2022·全国·高三专题练习）已知全集，则（ ）
A．B．C．D．
【答案】D
【解析】，故选:D.
3．（2022·全国·专题练习）（多选）已知全集U的两个非空真子集A，B满足，则下列关系一定正确的是（ ）
A．B．
C．D．
【答案】CD
【解析】
令，，，满足，但，，故A，B均不正确；由，知，∴，∴，
由，知，∴，故C，D均正确.故选：CD.
考点四 求参
【例4-1】（2022·湖南师大附中）已知集合，，若，则B=（ ）
A．B．C．D．
【答案】B
【解析】由题意知：2是的一个解，所以，则，
故.故选：B.
【例4-2】（2022·全国·高三专题练习（理））设，，若，则实数的值不可以是（ ）
A．0B．C．D．2
【答案】D
【解析】由题意，，因为，所以，若，则，满足题意；
若，则，因为，所以或，则或.
综上：或或.故选：D.
【例4-3】（2022·云南师大附中）已知集合，，且，则实数的所有值构成的集合是（ ）
A．B．C．D．
【答案】D
【解析】因为，由可得.
当时，，合乎题意；
当时，，则或，解得或.
因此，实数的取值集合为.故选：D.
【例4-4】（2022·贵州毕节·高一期末）已知集合或，，若，则实数a的取值范围是（ ）
A．B．
C．D．
【答案】B
【解析】因为集合或，，，所以．故选：B．
【例4-5】（2022·全国·池州市第一中学高一开学考试）已知集合，．
(1)当时，求；
(2)若______，求实数a的取值范围．
请从①，②，③，这三个条件中选一个填入（2）中横线顶处，并完成第（2）问的解答．（如果选择多个条件分别解答，按第一个解答计分）
【答案】(1)
(2)答案不唯一，具体见解析
【解析】(1)由题意得，．
当时，，∴．
(2)选择①：
∵，∴．
当时，，不满足，舍去；
当时，，要使，则，解得；
当时，，此时，，舍去，
综上，实数a的取值范围为．
选择②：
当时，，满足；
当时，，要使，则，解得；
当时，，此时，，
综上，实数a的取值范围为．
选择③：
当时，，，∴，满足题意；
当时，，，
要使，则，解得；
当时，，，
此时，满足题意，
综上，实数a的取值范围为．
【一隅三反】
1．（2022·陕西·西北工业大学附属中学模拟预测（理））已集合，集合，，则实数a的取值范围为（ ）
A．B．C．D．
【答案】B
【解析】因为集合，集合，，所以.故选：B.
2．（2022·广东·深圳实验学校高一期中）已知集合，，若满足，则的值为( )
A．或5B．或5C．D．5
【答案】C
【解析】∵，∴9∈A，或，解得或或，
当时，，，此时，不符合题意；
当时，，集合不满足元素的互异性，不符合题意；
当时，，，此时，符合题意；
综上，故选：C．
3．（2022·全国·高三专题练习）已知集合，若，则x的不同取值个数为（ ）
A．1B．2C．3D．4
【答案】C
【解析】因为，所以.所以或.
由，解得，由，解得或.
注意当时，，集合A、B中元素不满足互异性，
所以符合题意的x为或，不同的取值个数是3个.故选：C.
4．（2022·浙江）已知全集，集合.若，则（ ）
A．4B．3C．2D．0
【答案】A
【解析】因为，又，
所以，即且，又，所以；故选：A
5．（2022·江苏·扬州中学高一开学考试）已知集合.
(1)在①，②，③这三个条件中选择一个条件，求；
(2)若，求实数的取值范围.
【答案】(1)答案见解析(2)
【解析】(1)解：若选择①:当时，，
因为，所以.
若选择②:当时，，
因为，所以.
若选择③:当时，，
因为，所以.
(2)
解：因为，
所以.
因为，所以，
当时，；
当时，，
即；
综上，.
6．（2022·云南玉溪·高一期末）已知集合，．
(1)若，求；
(2)在①，②，③，这三个条件中任选一个作为已知条件，求实数的取值范围．
【答案】(1)(2)答案见解析
【解析】(1)因为，所以，
又因为，所以．
(2)若选①：则满足或，
所以的取值范围为或．
若选②：所以或，
则满足，所以的取值范围为．
若选③： 由题意得，
则满足
所以的取值范围为
考点五 韦恩图
【例5】（2022·江西萍乡）如图，全集，，，则阴影部分表示的集合为（ ）
A．B．C．D．
【答案】D
【解析】由图示可知，阴影部分可表示为,∵,∴,故选：.
【一隅三反】
1．（2022·安徽合肥）设全集，集合，，则下面Venn图中阴影部分表示的集合是（ ）
A．B．
C．D．
【答案】D
【解析】由题意,可知Venn图中阴影部分表示的集合是 ,故选：D
2．（2022·全国·模拟预测）已知全集，，，则图中阴影部分表示的集合是（ ）
A．B．C．D．
【答案】B
【解析】全集,
又因为，所以,而
所以阴影部分表示的集合是即为，
故选：B.
3．（2022·全国·高三专题练习（文））设U＝R，已知两个非空集合P，Q满足＝R，则（ ）
A．P∩Q＝RB．PQ
C．QPD．P∪Q＝R
【答案】B
【解析】满足＝R，则P，Q，U三个集合如图所示：
即PQ，故选：B.