2024贵州中考数学一轮知识点复习 第6讲 一次方程（组）及其应用（课件）

这是一份2024贵州中考数学一轮知识点复习 第6讲 一次方程（组）及其应用（课件），共31页。PPT课件主要包含了考点精讲，等式的性质，b±c，一元一次方程及其解法，解法步骤与注意事项，－2x－2＝6x，二元一次方程组的解法，加减消元法，行程问题，追及问题等内容，欢迎下载使用。
1. (2023三州联考14题3分)已知 是方程组 的解，则a＋b的值为___．
解二元一次方程组(黔西南州2023.14，黔东南州2023.14)
2. (2022毕节9题3分)已知关于x，y的方程x2m－n－2＋4ym＋n＋1＝6是二元一次方程，则m，n的值为(　　)A. m＝1，n＝－1　　　 　　B. m＝－1，n＝1C. m＝ ，n＝－ D. m＝－ ，n＝
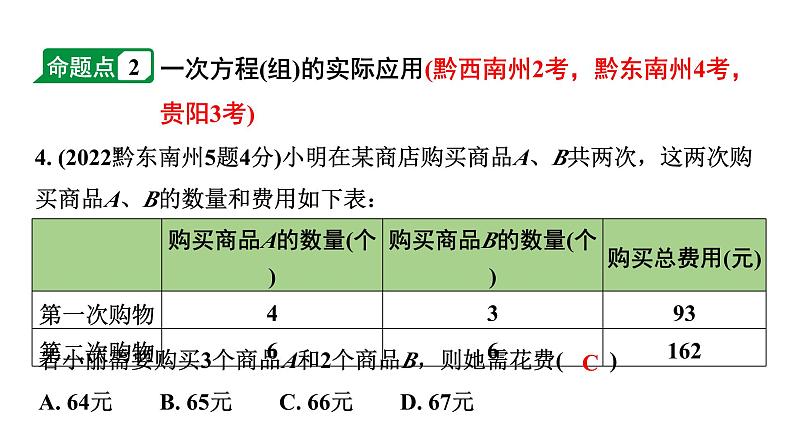
一次方程(组)的实际应用(黔西南州2考，黔东南州4考，贵阳3考)
4. (2022黔东南州5题4分)小明在某商店购买商品A、B共两次，这两次购买商品A、B的数量和费用如下表：
若小丽需要购买3个商品A和2个商品B，则她需花费(　　)A. 64元　　B. 65元　　C. 66元　　D. 67元
5. (2023三州联考15题3分·源自北师七上P146第2题)某品牌旗舰店平日将某商品按进价提高40%后标价，在某次电商购物节中，为促销该商品，按标价8折销售，售价为2240元，则这种商品的进价是_______元．
6. (2022铜仁7题4分)我国古代名著《九章算术》中有一题：“今有凫起南海，七日至北海；雁起北海，九日至南海．今凫雁俱起，问何日相逢？”(凫：野鸭)设野鸭与大雁从南海和北海同时起飞，经过x天相遇，可列方程为(　　)A. (9－7)x＝1 B. (9＋7)x＝1C. ( － )x＝1 D. ( ＋ )x＝1
7. (2020黔南州8题4分)某超市正在热销一种商品，其标价为每件12元，打8折销售后每件可获利2元，该商品每件的进价为(　　)A. 7.4元 　 B. 7.5元 　 C. 7.6元 　 D. 7.7元8. (2020毕节12题3分)由于换季，商场准备对某商品打折出售，如果按原售价的七五折出售，将亏损25元，而按原售价的九折出售，将盈利20元，则该商品的原售价为(　　)A. 230元 B. 250元 C. 270元 D. 300 元
9. (2020黔南州19题3分)方程术是《九章算术》最高的数学成就．《九章算术》中记载：“今有牛五，羊二，直金十两；牛二、羊五，直金八两．问牛、羊各直金几何？”意思是：“假设有5头牛、2只羊，值金10两；2头牛，5只羊，值金8两．问每头牛、每只羊各值金多少两？”若设每头牛值金x两，每只羊值金y两，则可列方程组为____________．
10. (2022六盘水24题10分)甲乙两个施工队在六安(六盘水—安顺)城际高铁施工中，每天甲队比乙队多铺设100米钢轨，甲队铺设5天的距离刚好等于乙队铺设6天的距离，若设甲队每天铺设x米，乙队每天铺设y米．(1)依题意列出二元一次方程组；
(2)求出甲乙两施工队每天各铺设多少米？
一次方程(组)及其应用
【对接教材】人教：七上第三章P77－P112， 七下第八章P87－P112; 北师：七上第五章P129－P154， 八上第五章P102－P134.
性质1：等式两边加(或减)同一个数(或式子)，结果仍相等：如果a＝b，那么a±c＝_____ 移项性质2：等式两边乘同一个数，结果仍相等：如果a＝b，那么___＝bc 去分母(方程两边同乘各分母的最小公倍数)性质3：等式两边除以同一个不为0的数，结果仍相等：如果a＝b，那么___＝ (c≠0) 系数化为1
定义：只含有一个未知数(一元)，未知数的次数都是1(一次)的整式方程
6－2(x＋1)＝6x
二元一次方程（组）及其解法
二元一次方程：含有两个未知数(二元)，并且含有未知数的项的次数都是___的整式方程，形如ax＋by＝c(a、b、c为常数，且a≠0，b≠0)二元一次方程组：方程组中有两个未知数，含有每个未知数的项的次数都是1，并且一共有两个方程
1.代入消元法：当方程组中一个方程的常数项为0或某一个未知数的系数是1或－1时，选择代入消元法较为简单
(1)当方程组中同一个未知数的系数相反或相同时，采用加减消元法较为简单；(2)当系数不相反也不相同时，可通过找系数的最小公倍数，将系数变成相反或相同，采用加减消元法较为简单
一次方程（组）的实际应用常见等量关系
工程问题：工作量＝工作效率×__________
基本量之间的关系：路程＝速度×时间相遇问题：总路程＝甲走的路程___乙走的路程
同地不同时出发：前者走的路程＝追者走的路程同时不同地出发：前者走的路程＋出发前两者间的距离＝追者走的路程
例1　解方程组解法一：加减消元法
解：②×3，得__________③，③＋①得________，解得_____，将x＝___代入①，
得_________，解得______，∴原方程组的解为_______．
【解题依据】由②变形到③依据的等式性质是____________________________________________．
解法二：代入消元法解：将②变形为y＝______④，将④代入①中，得________________，解得______，将x＝___代入④，得_____，
【解题依据】由②变形到④依据的等式性质是______________________________________________．
2x＋3(3x－2)＝5
∴原方程组的解为_______．
去同一个数，等式仍成立
(1)　　　　 　
例2　为加强美育教育，学校计划开设书法特色课程，需购买毛笔、墨汁两种文具供学校师生使用．已知学校在商场共购买毛笔和墨汁两种文具两次，①第一次购买毛笔60根，墨汁40瓶，共花费1200元，②第二次购买毛笔40根，墨汁30瓶，共花费850元．(1)求毛笔与墨汁的单价分别为多少元；
【分层分析】设毛笔的单价为x元，墨汁的单价为y元，则第一次购买毛笔的花费为____元，购买墨汁的花费为____元，由①可列关系式为________________；同理由②可列关系式为______________，解方程组即可；
60x＋40y＝1200
40x＋30y＝850
(2)若学校计划从该商场③购买毛笔与墨汁两种文具的总数量为90，且已知计划购买④毛笔的数量为墨汁的2倍，请你预计学校此次购买毛笔与墨汁的总费用为多少元；
【分层分析】设计划购买毛笔a根，购买墨汁b瓶，由③可列关系式为_________，由④可列关系式为_______，解方程组即可得到计划购买毛笔与墨汁两种文具的数量，再结合(1)中的结论即可求得预计购买文具的总费用；
(3)若学校计划再次从该商场购买毛笔和墨汁，且经双方议价，⑤毛笔和墨汁两种文具均可按9折销售，⑥学校共需付款1440元，且⑦此次购买毛笔的根数比墨汁的瓶数多10，求学校计划再次购买毛笔和墨汁两种文具的数量．
【分层分析】设计划再次购买毛笔p根，墨汁q瓶，由⑤得毛笔打折后的售价为_____________元，墨汁打折后的售价为_______________元，由⑥可列关系式为________________，由⑦可列关系式为__________，解方程组即可．
15×90%＝13.5
9p＋13.5q＝1440
1. 某电器商场销售进价分别为120元、190元的A、B两种型号的电风扇，第一批货两周销售完毕，如表所示是近两周的销售情况(进价、售价均保持不变，利润＝销售收入－进货成本)：
(1)求A、B两种型号的电风扇的销售单价；
解：(1)设A种型号的电风扇的销售单价为x元/台，B种型号的电风扇的销售单价为y元/台，
答：A种型号的电风扇的销售单价为150元/台，B种型号的电风扇的销售单价为260元/台；