






2024贵州中考数学一轮知识点复习 第12讲 一次函数的实际应用(课件)
展开例1 某工程队铺一条公路,一天可铺300米,则该工程队所铺公路总长度y(米)与其施工时间x(天)之间的关系是__________.
根据题意,列函数关系式:
【解题依据】工作总量=工作效率×工作时间.
例2 某报亭老板以每份0.5元的价格从报社购进某种报纸若干份,并以每份0.8元的价格销售.设这次买卖中该老板获利y元,老板销售的报纸数量为x份,则y与x之间的函数关系式为_________.
【解题依据】利润=(售价-进价)×销量.
例3 小明周末骑自行车从家里出发去离家8千米的图书馆,匀速骑行一段路程后,因为天气炎热,在路边阴凉地休息了一会儿,然后继续以同一速度骑行到达图书馆.在整个过程中,小明离家的距离y(千米)与时间x(分钟)的对应关系如图所示,则图中a=____,小明休息完继续出发到他到达图书馆期间,y与x之间的函数关系式为________________________.
【解题依据】路程=速度×时间,待定系数法求解析式.
y=0.25x-1.25(15<x≤37)
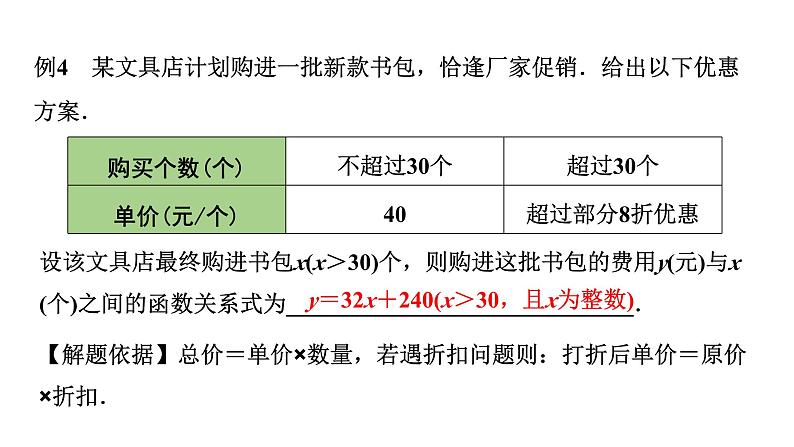
例4 某文具店计划购进一批新款书包,恰逢厂家促销.给出以下优惠方案.
设该文具店最终购进书包x(x>30)个,则购进这批书包的费用y(元)与x(个)之间的函数关系式为______________________________.
【解题依据】总价=单价×数量,若遇折扣问题则:打折后单价=原价×折扣.
y=32x+240(x>30,且x为整数)
例5 为迎接六一儿童节,某慈善团队计划①订购900件玩具送给福利院的小朋友们.现了解到某玩具专卖店有A、B两种热销的玩具,已知②A种玩具的单价为30元,B种玩具的单价为50元,设购买A种玩具x件,购买A、B两种热销的玩具所需要的总费用为y元.(1)求y关于x的函数关系式,并写出自变量的取值范围;
【分层分析】设购买A种玩具x件,由①知,则购买B种玩具的数量为________件,购买A种玩具需要的费用可表示为_____;购买B种玩具需要的费用可表示为___________;总费用为_________________;
y=-20x+45000
解:(1)由题知购买A种玩具x件,则购买B种玩具(900-x)件,购买A、B两种热销的玩具所需要的的总费用为y元,根据题意,可得y=30x+50(900-x)=-20x+45000(0<x<900,且x为整数);
(2)若③计划订购B种玩具的数量不少于A种玩具的 ,求该慈善团队订购A种玩具多少件时,总花费最少?最少花费为多少元?
【分层分析】由(1)知订购A种玩具x件,订购B种玩具________件,由③可列不等式为___________,由(1)知,订购A、B两种玩具的总费用y关于x的函数解析式为_________________,利用一次函数的性质即可求解;
(2)由(1)得y=-20x+45000,∵-20<0,∴y随x的增大而减小,∴当x取最大值时,y有最小值,
(3)该玩具专卖店从甲、乙两个玩具厂商中的一家进货,且两家厂商给出的A种玩具进价均为20元,B种玩具进价均为30元.由于订购量大,两个玩具厂分别给予一定的优惠:④甲玩具厂表示,A、B两种玩具的进价统一打9折;⑤乙玩具厂表示,A种玩具价格不变,B种玩具订货超过200件,超出的部分打8折.若该专卖店计划购进B种玩具的数量超过200件,请你帮该玩具专卖店分析在哪个玩具厂进货更合算.
【分层分析】设该玩具专卖店购进A种玩具a件,B种玩具购进________件,由④知,在甲玩具厂进货的费用Q1为____________元,由⑤知,在乙玩具厂进货的费用Q2为____________元,分别令Q1>Q2,Q1=Q2,Q1<Q2,计算不同情况下的a的取值范围,并选择方案.
(3)设该玩具专卖店购进A种玩具a件,B种玩具购进(900-a)件,在甲玩具厂进货共花费Q1元,在乙玩具厂进货共花费Q2元,则在甲玩具厂进货需花费Q1=0.9[20a+30(900-a)]=-9a+24300,在乙玩具厂进货需花费Q2=20a+30×200+(900-200-a)×30×0.8=-4a+22800,
令-9a+24300=-4a+22800,解得a=300,∵-4>-9,∴当a<300时,Q1>Q2,当a=300时,Q1=Q2,当a>300时,Q1<Q2,答:当购进A种玩具的数量小于300件时,在乙玩具厂进货更合算;当购进A种玩具的数量等于300件时,在甲、乙两个玩具厂进货均可;当购进A种玩具的数量大于300件且小于700件时,在甲玩具厂进货更合算.
类型一 行程问题(黔西南州2023.24)
1. (2023黔西南州24题14分)赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B.在整个行程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示.请结合图象解答下列问题:
(1)起点A与终点B之间相距多远?
解:(1)由题图可知,起点A与终点B之间相距3000米;(3分)
(2)哪支龙舟队先出发?哪支龙舟队先到达终点?
(2)由题图可知,甲龙舟队先出发,乙龙舟队先到达终点;(6分)
(3)分别求甲、乙两支龙舟队的y与x函数关系式;
(4)甲龙舟队出发多长时间时两支龙舟队相距200米?
2. (2023黔西南州19题3分)如图,小明购买一种笔记本所付款金额y(元)与购买量x(本)之间的函数图象由线段OB和射线BE组成,则一次购买8个笔记本比分8次购买每次购买1个可节省____元.
类型二 分段计费问题(黔西南州2023.19)
3. (2023黔西南州24题14分)某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过12吨(含12吨)时,每吨按政府补贴优惠价收费;每月用水量超过12吨,超过部分每吨按市场调节价收费,小黄家1月份用水24吨,交水费42元.2月份用水20吨,交水费32元. (1)求每吨水的政府补贴优惠价和市场调节价分别是多少元;
(2)设每月用水量为x吨,应交水费为y元,写出y与x之间的函数关系式;
(3)小黄家3月份用水26吨,他家应交水费多少元?
(3)当x=26时,y=2.5×26-18=65-18=47(元).答:3月份他家应交水费47元.(14分)
类型三 方案问题(黔西南州2021.24)
4. (2021黔西南州24题12分)甲、乙两家水果商店,平时以同样的价格出售品质相同的樱桃.春节期间,甲、乙两家商店都让利酬宾.甲商店的樱桃价格为60元/kg;乙商店的樱桃价格为65元/kg,若一次购买2 kg以上,超过2 kg部分的樱桃价格打8折.(1)设购买樱桃x kg,y甲,y乙(单位:元)分别表示顾客到甲、乙两家商店购买樱桃的付款金额,求y甲,y乙关于x的函数解析式;
解:(1)由题意得,y甲=60x(x≥0),当0≤x≤2时,y乙=65x,当x>2时,y乙=65×2+(x-2)×65×0.8=52x+26,∴y乙= ;(5分)
(2)春节期间,如何选择甲、乙两家商店购买樱桃更省钱?
(2)当0≤x≤2时,∵60x<65x,∴当购买樱桃不超过2 kg时,去甲商店买樱桃更省钱;当x>2时,令52x+26=60x,得x=3.25,∴当购买樱桃3.25 kg时,去两家商店买樱桃的花费相同;令52x+26<60x,得x>3.25,∴当购买樱桃超过3.25 kg时,去乙商店买樱桃更省钱;令52x+26>60x,得x<3.25,∴当购买樱桃超过2 kg且不超过3.25 kg时,去甲商店买樱桃更省钱.(12分)
5. (2023黔南州25题12分)都匀某校准备组织学生及家长代表到桂林进行社会实践活动,为便于管理,所有人员必须乘坐同一列高铁. 高铁单程票价格如下表所示,二等座学生票可打7.5折. 已知所有人员都买一等座单程火车票需6175元,都买二等座单程火车票需3150元;如果家长代表与教师的人数之比为2∶1.
(1)参加社会实践活动的老师、家长代表与学生各有多少人?
(2)由于各种原因,二等座单程火车票只能买x张(x<参加社会实践的总人数),其余的须买一等座单程火车票,在保证所有人员都有座位的前提下,请你设计最经济的购票方案,并写出购买单程火车票的总费用y与x之间的函数关系式;
(2)由(1)知,所有参与人员总共有65人,其中学生有50人,①当50≤x<65时,最经济的购票方案为:买二等座学生票50张,买二等座成人票(x-50)张,买一等座火车票(65-x)张.
. . . . . . . .
∴火车票的总费用(单程)y与x之间的函数关系为:y=60×0.75×50+60(x-50)+95(65-x),即y=-35x+5425(50≤x<65),(6分)②当0<x<50时,最经济的购票方案为:买二等座学生票共x张,其余所有人购买一等座单程火车票共(65-x)张.∴火车票的总费用(单程)y与x之间的函数关系为:y=60×0.75x+95(65-x),即y=-50x+6175(0<x<50),(8分)∴购买火车票的总费用(单程)y与x之间的函数关系式是y= ;(9分)
(3)在(2)的方案下,请求出当x=30时,购买单程火车票的总费用.
(3)∵x=30<50,(10分)∴y=-50x+6175=-50×30+6175=4675.(11分)答:当x=30时,购买单程火车票的总费用为4675元.(12分)
类型四 最值问题(黔西南州2考,黔东南州3考,贵阳2021.22)
6. (2023黔西南州24题14分)我州某养殖场计划购买甲、乙两种鱼苗600条,甲种鱼苗每条16元,乙种鱼苗每条20元.相关资料表明:甲、乙两种鱼苗的成活率分别为80%,90%.(1)若购买这两种鱼苗共用去11000元,则甲、乙两种鱼苗各购买多少条?
(2)若要使这些鱼苗的总成活率不低于85%,则乙种鱼苗至少购买多少条?
(2)设购买乙种鱼苗m条,则购买甲种鱼苗(600-m)条,由题意得,90%m+80%(600-m)≥85%×600,(8分)解得m≥300. 答:至少购买乙种鱼苗300条;(9分)
(3)在(2)的条件下,应如何选购鱼苗,使购买鱼苗的总费用最低?最低费用是多少?
(3)设购买鱼苗的总费用为Z元,则Z=20m+16(600-m)=4m+9600.(11分)∵4>0,∴Z随m的增大而增大,又∵m≥300,∴当m=300时,Z有最小值. ∴Z最小=4×300+9600=10800(元).600-m=300(条),答:当购买甲种鱼苗300条,乙种鱼苗300条时,总费用最低,最低费用为10800元.(14分)
7. (2023黔东南州23题12分)某校为了在九月份迎接高一年级的新生,决定将学生公寓楼重新装修,现学校招用了甲、乙两个工程队,若两队合作,8天就可完成该项工程;若由甲队先单独做3天后,剩余部分由乙队单独做需要18天才能完成.(1)求甲、乙两队工作效率分别是多少?
(2)甲队每天工资3000元,乙队每天工资1400元,学校要求在12天内将学生公寓楼装修完成.若完成该工作甲队工作m天,乙队工作n天,求学校需支付的总工资w(元)与甲队工作天数m(天)的函数关系式,并求出m的取值范围及w的最小值.
∵学校要求12天内完成任务,∴m≤12,n≤12,即24-2m≤12,∴6≤m≤12.∵w=200m+33600,200>0,∴当m=6时,w有最小值,此时w=200×6+33600=34800(元).答:w=200m+33600,m的取值范围为6≤m≤12,其中当m=6时,w有最小值,最小值为34800元.(12分)
8. (2022黔西南州24题14分)随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车,去年销售总额为8万元,今年该型号自行车每辆售价比去年降低200元.若今年该型号自行车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:(1)A型自行车去年每辆售价多少元?
解得x=2000,(4分)检验,当x=2000时,x(x-200)≠0,∴x=2000是原分式方程的解且符合实际意义.(5分)答:A型自行车去年每辆售价为2000元;(6分)
(2)该车行今年计划新进一批A型自行车和新款B型自行车共60辆,且B型自行车的进货数量不超过A型自行车进货数量的两倍.已知A型自行车和B型自行车的进货价格每辆分别为1500元和1800元,计划B型自行车销售价格为每辆2400元,应如何组织进货才能使这批自行车销售获利最多?
(2)设今年新进A型自行车a辆,则应进B型自行车(60-a)辆,获利y元.(7分)由(1)可知,A型自行车今年每辆售价2000-200=1800元.由题意得y=(1800-1500)a+(2400-1800)(60-a)=-300a+36000.(9分)
∵B型自行车的进货数量不超过A型自行车进货数量的两倍,∴60-a≤2a,解得a≥20,(10分)∵在y=-300a+36000中,-300<0,∴y随a的增大而减小,∴当a=20时,y有最大值,(12分)此时,B型自行车的数量为60-20=40辆.答:应新进A型自行车20辆,B型自行车40辆,才能使这批自行车销售获利最多.(14分)
9. (2021黔东南州24题12分)黔东南州某销售公司准备购进A、B两种商品,已知购进3件A商品和2件B商品,需要1100元;购进5件A商品和3件B商品,需要1750元.(1)求A、B两种商品的进货单价分别是多少元?
(2)若该公司购进A商品200件,B商品300件,准备把这些商品全部运往甲、乙两地销售.已知每件A商品运往甲、乙两地的运费分别为20元和25元;每件B商品运往甲、乙两地的运费分别为15元和24元.若运往甲地的商品共240件,运往乙地的商品共260件.①设运往甲地的A商品为x(件),投资总费用为y(元),请写出y与x的函数关系式;
(2)①根据题意得,总运费=20x+25(200-x)+15(240-x)+24[260-(200-x)]=4x+10040,购进商品总的费用=200×200+250×300=115000,∵投资总费用=购进商品总的费用+运费,∴y=4x+10040+115000=4x+125040(0≤x≤200);
②怎样调运A、B两种商品可使投资总费用最少?最少费用是多少元?(投资总费用=购进商品总的费用+运费)
②∵y=4x+125040(0≤x≤200),∴y随x的增大而增大,∴当x=0时,y的值最小,为125040,答:调运甲地240件B商品,调运乙地200件A商品,60件B商品,这种方案投资总费用最少,最少费用为125040元.(12分)
10. (2021贵阳22题10分)为庆祝“中国共产党的百年华诞”,某校请广告公司为其制作“童心向党”文艺活动的展板、宣传册和横幅,其中制作宣传册的数量是展板数量的5倍,广告公司制作每件产品所需时间和利润如下表:
(1)若制作三种产品共计需要25小时,所获利润为450元,求制作展板、宣传册和横幅的数量;
(2)若广告公司所获利润为700元,且三种产品均有制作,求制作三种产品总量的最小值.
11. (2021铜仁23题12分)某快递公司为了提高工作效率,计划购买A、B两种型号的机器人来搬运货物,已知每台A型机器人比每台B型机器人每天多搬运20吨,并且3台A型机器人和2台B型机器人每天共搬运货物460吨.(1)求每台A型机器人和每台B型机器人每天分别搬运货物多少吨?
(2)每台A型机器人售价3万元,每台B型机器人售价2万元,该公司计划采购A、B两种型号的机器人共20台,必须满足每天搬运的货物不低于1800吨,请根据以上要求,求出A、B两种机器人分别采购多少台时,所需费用最低?最低费用是多少?
(2)设A型机器人采购x台,则B型机器人采购(20-x)台,所需费用为y万元,由题意知:y=3x+2(20-x),即y=x+40,∵100x+80(20-x)≥1800,∴x≥10,
∵y=x+40,1>0,∴y随x的增大而增大,∴当x=10时,所需费用最低,最低费用为50万元.此时20-x=10,答:A型机器人采购10台,B型机器人采购10台时,所需费用最低,最低费用是50万元.(12分)
12. (2022安顺21题10分)安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售.为了让顾客得到更大的实惠,现决定降价销售.已知这种干果销售量y(千克)与每千克降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示:(1)求y与x之间的函数关系式;
解:(1)设一次函数关系式为y=kx+b,由题图知,当x=2时,y=120,当x=4时,y=140,代入y=kx+b得 ,(2分)解得 ,∴y=10x+100(0<x<20);(4分)
2024贵州中考数学一轮知识点复习 第11讲 一次函数的图象与性质(课件): 这是一份2024贵州中考数学一轮知识点复习 第11讲 一次函数的图象与性质(课件),共27页。PPT课件主要包含了第4题图,y=-2x,第7题图,y=2x+3,第9题图,第10题图,一次函数的图象与性质,考点精讲,k>0⇔,k<0⇔等内容,欢迎下载使用。
2024贵州中考数学一轮知识点复习 第8讲 分式方程及其应用(课件): 这是一份2024贵州中考数学一轮知识点复习 第8讲 分式方程及其应用(课件),共34页。PPT课件主要包含了分式方程及其应用,考点精讲,整式方程,――→,x=a,实际应用,一般步骤,常考类型及等量关系,分式方程及其实际应用,x-2等内容,欢迎下载使用。
第12讲一次函数的实际应用课件---2024年中考数学一轮复习: 这是一份第12讲一次函数的实际应用课件---2024年中考数学一轮复习,共31页。PPT课件主要包含了综合模拟练,基础全练,挑战高分,中考创新练,或116等内容,欢迎下载使用。












