



2024贵州中考数学一轮知识点复习 第20讲 三角形及其性质(课件)
展开1. (2023三州联考7题4分·源自北师七下P86第1题)在下列长度的三条线段中,不能组成三角形的是( )A. 2 cm,3 cm,4 cm B. 3 cm,6 cm,6 cmC. 2 cm,2 cm,6 cm D. 5 cm,6 cm,7 cm
三角形的边角关系(黔西南州3考,黔东南州2考)
2. (2021黔西南州16题3分)三角形两边的长分别为2和5,第三边的长是方程x2-8x+15=0的根,则该三角形的周长为________.
3. (2022毕节5题3分)已知一个三角形的两边长分别为8和2,则这个三角形的第三边长可能是( )A. 4 B. 6C. 8 D. 10
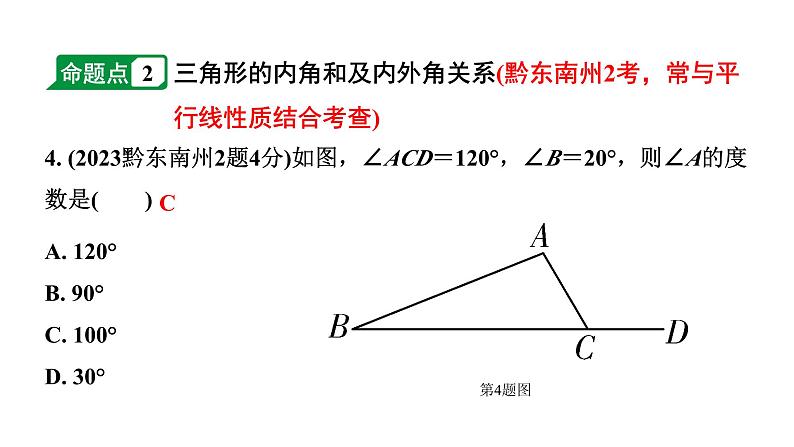
4. (2023黔东南州2题4分)如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
A. 120°B. 90°C. 100°D. 30°
三角形的内角和及内外角关系(黔东南州2考,常与平行线性质结合考查)
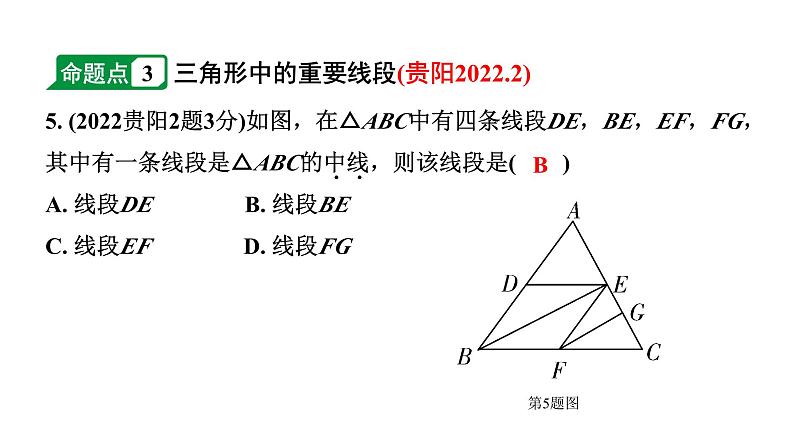
5. (2022贵阳2题3分)如图,在△ABC中有四条线段DE,BE,EF,FG,其中有一条线段是△ABC的中线,则该线段是( )A. 线段DE B. 线段BEC. 线段EF D. 线段FG
三角形中的重要线段(贵阳2022.2)
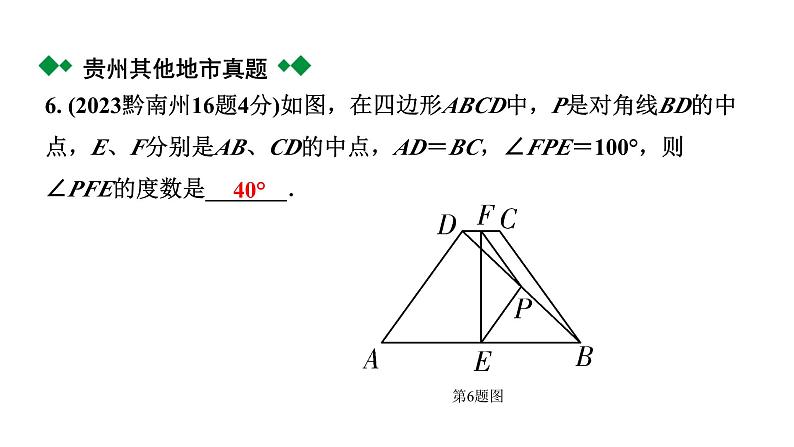
6. (2023黔南州16题4分)如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠FPE=100°,则∠PFE的度数是_______.
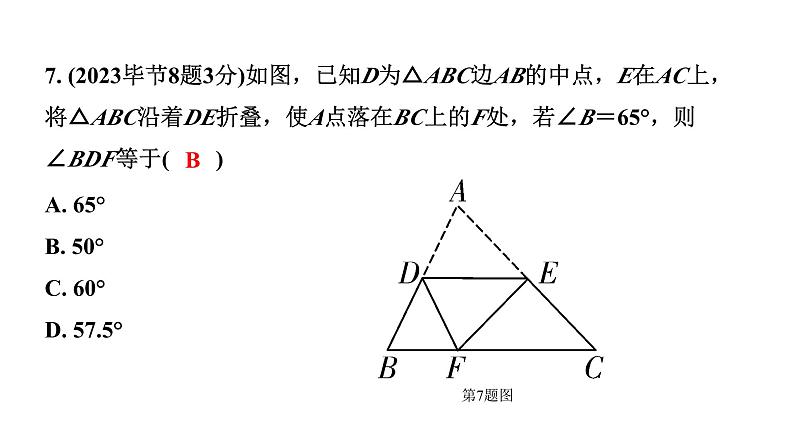
7. (2023毕节8题3分)如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处,若∠B=65°,则∠BDF等于( )
A. 65°B. 50°C. 60°D. 57.5°
8. (2022毕节6题3分)到三角形三个顶点的距离都相等的点是这个三角形的( )A. 三条高线的交点B. 三条角平分线的交点C. 三条中线的交点D. 三条边的垂直平分线的交点
9. (2023遵义10题3分)如图,△ABC的面积是12,点D、E、F、G分别是BC、AD、BE、CE的中点,则△AFG的面积是( )A. 4.5 B. 5 C. 5.5 D. 6
10. (2023铜仁7题4分)如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,点E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH的周长为( )A. 12 B. 14C. 24 D. 21
11. (2023遵义12题3分)如图,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC=15,则FC的长为( )A. 11 B. 12 C. 13 D. 14
12. (2023铜仁17题4分)如图,∠ACB=90°,D为AB中点,连接DC并延长到点E,使CE= CD,过点B作BF∥DE交AE的延长线于点F,若BF=10,则AB的长为_____.
【对接教材】人教:八上第十一章P1-P29、第十二章P48-P50; 北师:七下第四章P80-P91, 八上第七章P178-P183, 八下第六章P150-P152.
底与腰不相等的等腰三角形等边三角形
不等边三角形:三边互不相等的三角形
按角分:锐角三角形、直角三角形、钝角三角形
三边关系:_____________________________________________________
判断三条线段能否构成三角形,应将两条较短边的和与最长边作比较
三角形两边的和大于第三边,三角形
____________________________
(1)任意一个外角_______与它不相邻的两个内角的和 如∠ACD______∠A+∠B(2)任意一个外角________与它不相邻的任何一个内角 如∠ACD______∠A,∠ACD______∠B
三角形三个内角的和等于180°
边角关系:同一个三角形中,等边对等角,等角对_____,大边对大角,小边对小角
三角形的外心是三角形三条垂直平分线的交点,到三角形的三个顶点的距离相等.锐角三角形的外心在三角形的内部;直角三角形的外心是斜边的中点;钝角三角形的外心在三角形的外部.如右图,则有(1)AM=BM,BN=NC;(2)OM⊥AB,ON⊥BC;(3)OA=OB=OC
例1 如图,已知△ABC,AB=5,点D是BC上一点,连接AD
(1)若AC=3,则线段BC的长的取值范围为_________;(2)若∠B∶∠C∶∠CAB=5∶6∶7,且∠CDA=110°,则∠CAB的度数为______,∠DAB的度数为______;
(3)若点D、E分别为BC、AC的中点,则DE的长为________;
【解题依据】(3)问中用到的性质依据为__________________________________________________.
(4)若AD是△ABC的高线,BD=3,∠CAD=30°,则AC的长为____;
三角形的中位线平行于第三边,
(5)若AD是∠BAC的平分线,若AC=4,S△ABD=9,则△ABC的面积为_____;
【解题依据】(5)问中用到的性质依据为___________________________________.
角平分线上的点到角两边的
(6)若AD是△ABC的中线,S△ABD=6,则点C到AB的距离为______.
【解题依据】(6)问中用到的性质依据为__________________________________________.
中线将三角形分成面积相等
例2 如图①,在△ABC中,D、E分别为AB、AC的中点,连接DE.
(1)如图②,CF平分∠ACB,交DE于点F,∠EFC=15°,则∠AED的大小为_______;
(2)如图③,若点F为DE上一点,CF⊥AF,若AC=6,DF=2,则BC的长为______;(3)如图④,连接BE,CD交于点M,若S△ABC=6,则S△BCM=_____;
(4)如图⑤,P、Q分别为BE、CD的中点,连接DP,PQ,QE,若AB=8,AC=6,BC=10,则四边形DPQE的周长为_____.
2024贵州中考数学一轮知识点复习 第11讲 一次函数的图象与性质(课件): 这是一份2024贵州中考数学一轮知识点复习 第11讲 一次函数的图象与性质(课件),共27页。PPT课件主要包含了第4题图,y=-2x,第7题图,y=2x+3,第9题图,第10题图,一次函数的图象与性质,考点精讲,k>0⇔,k<0⇔等内容,欢迎下载使用。
2024贵州中考数学一轮知识点复习 第8讲 分式方程及其应用(课件): 这是一份2024贵州中考数学一轮知识点复习 第8讲 分式方程及其应用(课件),共34页。PPT课件主要包含了分式方程及其应用,考点精讲,整式方程,――→,x=a,实际应用,一般步骤,常考类型及等量关系,分式方程及其实际应用,x-2等内容,欢迎下载使用。
2024贵州中考数学一轮知识点复习 第7讲 一元二次方程及其应用(课件): 这是一份2024贵州中考数学一轮知识点复习 第7讲 一元二次方程及其应用(课件),共38页。PPT课件主要包含了x1=3x2=9,一元二次方程及其应用,考点精讲,b2-4ac,根的判别式,b2-4ac=0,b2-4ac0,实际应用常见类型,增长率问题,图形面积问题等内容,欢迎下载使用。












