2024贵州中考数学一轮知识点复习 第21讲 全等三角形（课件）

这是一份2024贵州中考数学一轮知识点复习 第21讲 全等三角形（课件），共28页。PPT课件主要包含了第1题图，第2题图，第3题图，第4题图，第5题图，第7题图，全等三角形，判定方法，已知两边相等，已知两角相等等内容，欢迎下载使用。
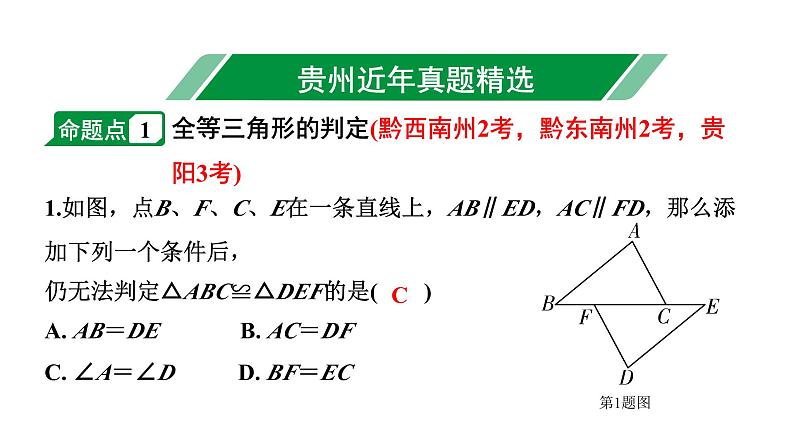
1.如图，点B、F、C、E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是(　　)
全等三角形的判定(黔西南州2考，黔东南州2考，贵阳3考)
A. AB＝DE B. AC＝DF C. ∠A＝∠D D. BF＝EC
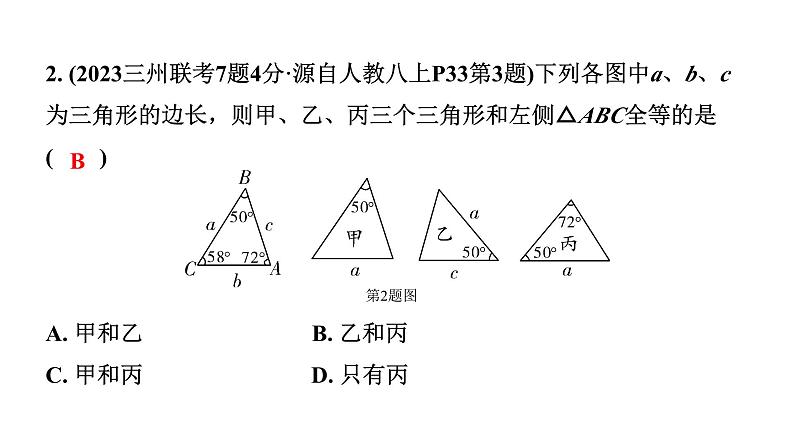
2. (2023三州联考7题4分·源自人教八上P33第3题)下列各图中a、b、c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是(　　)
A. 甲和乙　　　　　　　 B. 乙和丙C. 甲和丙 D. 只有丙
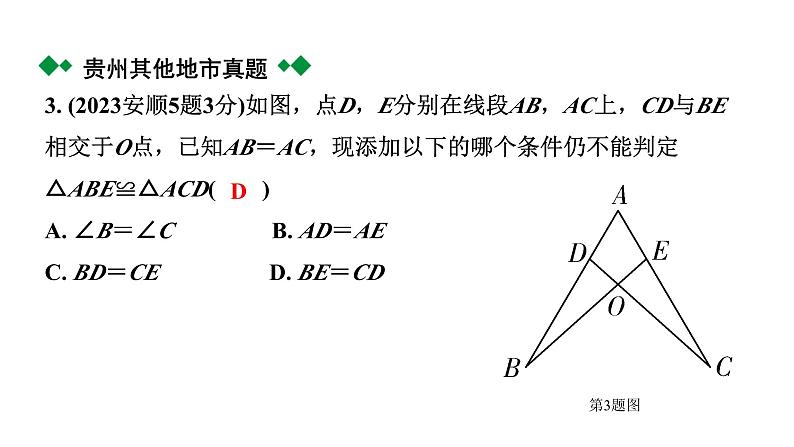
3. (2023安顺5题3分)如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB＝AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD(　　)A. ∠B＝∠C B. AD＝AEC. BD＝CE D. BE＝CD
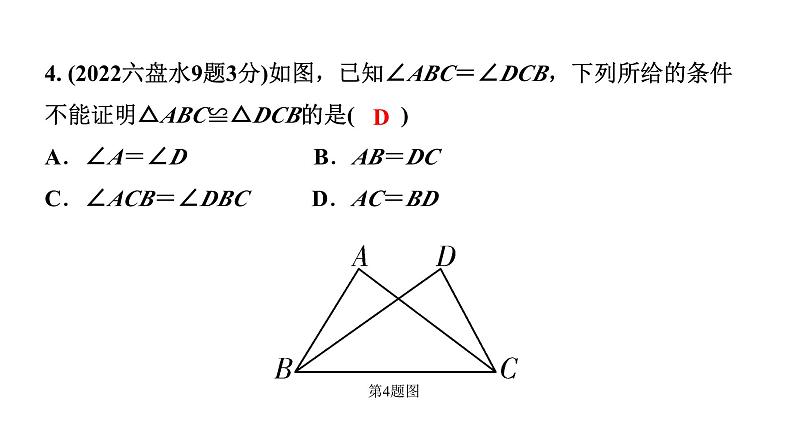
4. (2022六盘水9题3分)如图，已知∠ABC＝∠DCB，下列所给的条件不能证明△ABC≌△DCB的是(　　) A．∠A＝∠D B．AB＝DCC．∠ACB＝∠DBC D．AC＝BD
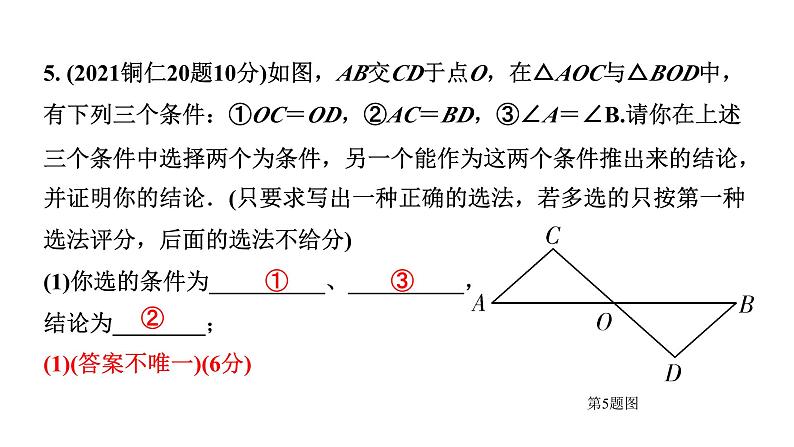
5. (2021铜仁20题10分)如图，AB交CD于点O，在△AOC与△BOD中，有下列三个条件：①OC＝OD，②AC＝BD，③∠A＝∠B.请你在上述三个条件中选择两个为条件，另一个能作为这两个条件推出来的结论，并证明你的结论．(只要求写出一种正确的选法，若多选的只按第一种选法评分，后面的选法不给分)(1)你选的条件为__________、__________，结论为________；
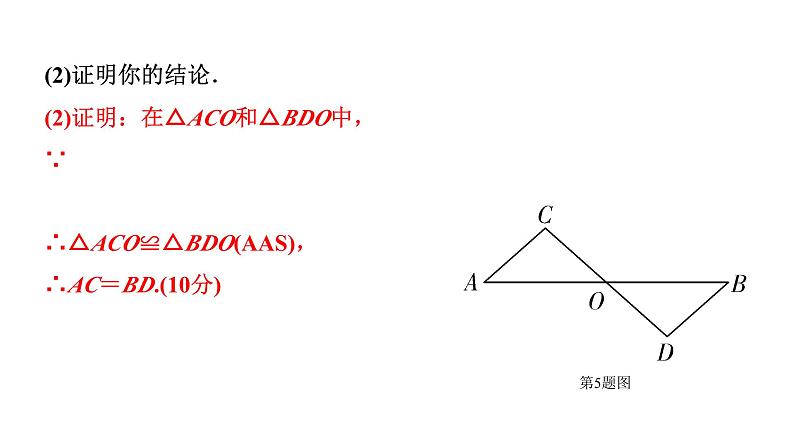
(1)(答案不唯一)(6分)
6. (2023铜仁22题10分)如图，已知点E、F分别是平行四边形ABCD对角线BD所在直线上的两点，连接AE、CF.请你添加一个条件，使得△ABE≌△CDF，并证明．
证明：方法一：添加BE＝DF(或DE＝BF)，证明如下：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，∴∠ABE＝∠CDF，∵BE＝DF，∴△ABE≌△CDF(SAS)．(10分)
方法二：添加∠E＝∠F(或AE∥CF)，证明如下：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，∴∠ABE＝∠CDF，∵∠E＝∠F，∴△ABE≌△CDF(AAS)．(10分)
方法三：添加∠EAB＝∠FCD(或∠EAD＝∠FCB)，证明如下：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，∴∠ABE＝∠CDF，∵∠EAB＝∠FCD，∴△ABE≌△CDF(ASA)．(10分)
全等三角形的性质(黔东南州2021.10)
7. (2021黔东南州10题4分)如图，在等腰直角△ACB中，∠C＝90°，点O是AB的中点，且AB＝ ，将一块直角三角板的直角顶点放在点O处，始终保持该直角三角板的两直角边分别与AC、BC相交，交点分别为点D、E，则CD＋CE等于(　　)
A. B. C. 2D.
【对接教材】人教：八上第十二章P30－P56； 北师：七下第四章P92－P104、P108－P110.
性质1：对应边________，对应角________性质2：对应线段(角平分线、中线、高线、中位线)相等，对应周长相等，对应面积相等
三边对应相等的两个三角形全等
两边及其夹角对应相等的两个三角形全等
两角及其夹边对应相等的两个三角形全等
两角分别相等且其中一组等角的对边相等的两个三角形全等
斜边和一条直角边分别相等的两个直角三角形全等
(1)两边和其中一边的对角相等的两个三角形不一定全等；(2)在判断两个三角形全等时，三组相等的元素中，至少有一组是边相等
找夹角→SAS找直角→HL或SAS找另一边→SSS
2.已知一边和一角相等
边为角的对边→找任一角→AAS
找已知角的另一邻边→SAS找已知边的另一邻角→ASA找已知边的对角→AAS
找夹边→ASA找任一角的对边→AAS
证明两条线段相等或者两个角相等时，常用的方法是证明这两条线段或者这两个角所在的三角形全等．当所证的线段或者角不在两个全等的三角形中时，可通过添加辅助线的方法构造全等三角形，先证全等，再运用全等的性质即可
例1　如图，将△ABC和△DEF按下图摆放，点A、B、D、E在同一直线上，AC∥DF，BC∥EF，要使△ABC≌△DEF，则还需添加的一个条件是_______________________．
【判定依据】______________________________________．
AB＝DE(答案不唯一)
例2　如图，将△ABC和△DEF按下图摆放(点E、F分别和点A、C重合)，∠B＝∠D，要使△ABC≌△EDF，则还需添加的一个条件是____________________________．
【判定依据】________________________________________________．
∠BAC＝∠DAC(答案不唯一)
两角及其中一角的对边对应相等的两个三角形全等
例3　如图，将△ABC和△DEF按下图摆放(点B与点E重合)，已知AB＝BD，BC＝BF，则还需添加的一个条件是_____________________，才能使△ABC≌△DEF.
【判定依据】__________________________________．
AC＝DF(答案不唯一)
三组边对应相等的两个三角形全等
例4　如图，将△ABC和△DEF按下图摆放(点B、C、F、E在同一直线上)，∠B＝∠E，BF＝EC，要使△ABC≌△DEF，则还需添加的一个条件是____________________________．
【判定依据】_______________________________________．
∠ACB＝∠DFE(答案不唯一)
例5　如图，将△ABC和△DEF按下图摆放(点F和点C重合)，点A，D，E在同一直线上，∠BAE＝∠BCE ＝90°，且BC ＝ CE，则还需添加的一个条件是________________________________，才能使△ABC≌△DEF，并加以证明．
∠BCA＝∠EFD(答案不唯一)
证明：∵∠BAE＝∠BCE＝90°，∴∠ABC＋∠AEF＝180°，∵∠DEF＋∠AEF＝180°，∴∠DEF＝∠ABC，
在△ABC和△DEF中，∴△ABC≌△DEF(ASA)．
1. 如图，AC平分∠BAD，∠B＝∠D＝90°，AD∥EC，若AD＝9，CE＝7，则BE的长为(　　)
A. 1B. 2C. 3D. 4
2. 如图，A，C，E三点在同一条直线上，且AC＝CE，BC∥DE，请你添加一个条件使得△ABC≌△CDE，并加以证明．
3. 在△ABC中，AB＝AC，∠BAC＝∠CDE＝60°，点D为AB边上的动点，CD＝ED，连接BE，EC.求证：AD＝BE.
证明：∵∠BAC＝60°，AB＝AC，∠CDE＝60°，CD＝ED，∴△ABC和△DCE都是等边三角形，∴AC＝BC，CD＝CE，∠ACB＝∠DCE＝60°，∴∠ACD＋∠DCB＝∠BCE＋∠DCB，∴∠ACD＝∠BCE，