初中数学浙教版七年级下册3.3 多项式的乘法试讲课ppt课件

这是一份初中数学浙教版七年级下册3.3 多项式的乘法试讲课ppt课件，文件包含浙教版数学七年级下册33《多项式的乘法》课件pptx、33多项式的乘法分层练习原卷版docx、浙教版数学七年级下册33《多项式的乘法》分层练习解析版docx等3份课件配套教学资源，其中PPT共31页， 欢迎下载使用。

1．熟练掌握单项式与多项式的乘法运算法则并进行单项式与多项式相乘的运算；2．熟练掌握多项式与多项式的乘法运算法则并进行多项式与多项式相乘的运算；3、学会根据多项式的乘积求字母或代数式的值；
单项式与单项式的乘法法则
单项式与单项式相乘，把它们的系数、同底数幂分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式.
思考：单项式与多项式的乘积该如何计算？多项式与多项式的乘积又该如何计算呢？
(m+n)(a+b)=?
学完本课，你就会算这两题的答案啦！
知识点一 单项式与多项式相乘
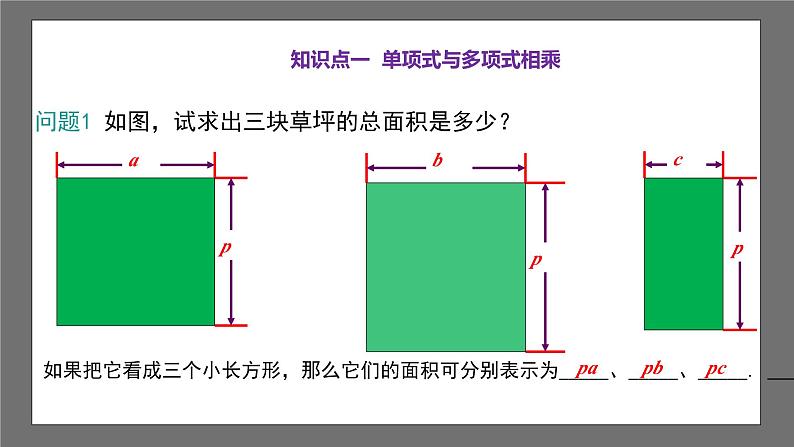
问题1 如图，试求出三块草坪的总面积是多少？
如果把它看成三个小长方形，那么它们的面积可分别表示为_____、_____、_____.
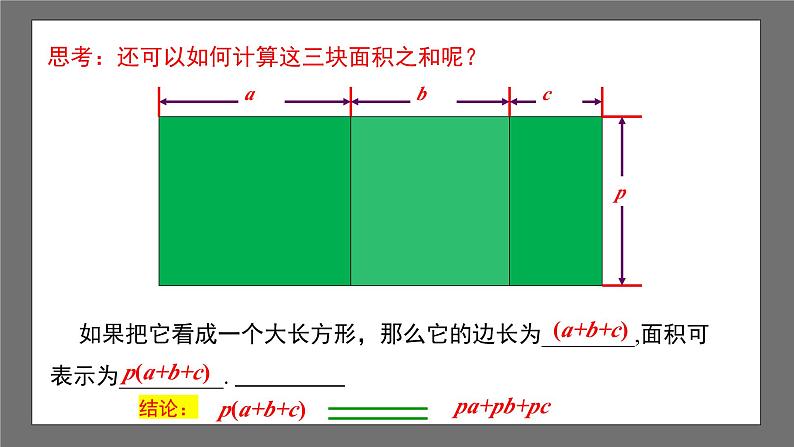
如果把它看成一个大长方形，那么它的边长为________,面积可表示为_________.
思考：还可以如何计算这三块面积之和呢？
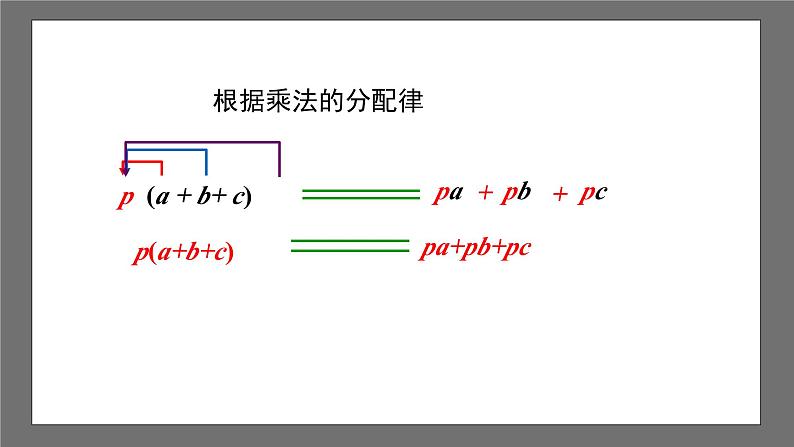
p (a + b+ c)
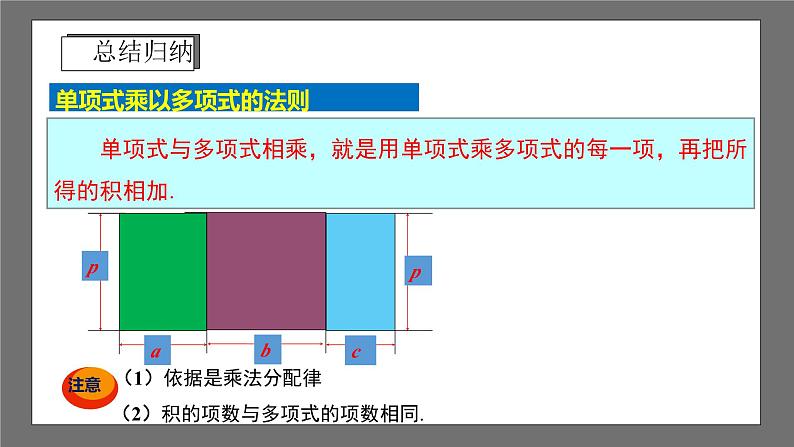
单项式乘以多项式的法则
单项式与多项式相乘，就是用单项式乘多项式的每一项，再把所得的积相加.
【详解】解：原式=-24a3+8a2-10a故选：C．
【点睛】本题考查了单项式乘以多项式，掌握单项式乘以多项式的运算法则是解题的关键．
【例2】已知3n-2m=-4，则代数式m(n-4)-n(m-6)的值为______．
【详解】解：∵3n-2m=-4，∴m(n-4)-n(m-6)=mn-4m-mn+6n=6n-4m=2(3n-2m)=2×(-4)=-8．故答案为：-8．
1．现定义运算“△”，对于任意有理数a，b，都有a△b=ab+b，例如：3△5=3×5+5=20，由此可知(x+1)△x等于（    ）A．x2 B．x2-2xC．x2+2xD．2x
【详解】解：根据题中的新定义得：(x+1)△x=(x-1)x+x=x2-x+x=x2，故选：A．
2．计算：(-3x2)2·(-x2+2x-1)．
【详解】解：(-3x2)2·(-x2+2x-1)=9x4·(-x2+2x-1)=-9x6+18x5-9x4．
知识点二 多项式与多项式相乘
问题2 某地区有一片林地，在一块原长m米，宽为a米的长方形林区增长了n米，加宽了b米，请你计算这块林区现在的面积.
你能用不同的形式表示所拼图的面积吗？
这块林区现在长为（m+n）米，宽为（a+b）米
m(a+b)+n(a+b)
ma+mb+na+nb
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积，故有：
(m+n)(a+b)=
如何进行多项式与多项式相乘的运算？
实际上，把(a+b)看成一个整体，有：
= ma+mb+na+nb
= m(a+b)+n(a+b)
若X=a+b，如何计算？
多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加.
多乘多，来计算，多项式各项都见面，乘后结果要相加，化简、排列才算完.
【例4】已知（x-2)(x+3)=x2+px+q，则qp=__________．
【详解】解：根据题意得，(x-2)(x+3)-x2-px-q=0，x2+x-6-x2-px-q=0，整理得(1-p)x-(6+q)=0，则p=1，q=-6qp=(-6)1=-6，故答案为：-6．
1．若(x-1)(x+3)=x2+mx+n，则m+n=（　　）A．-1 B．-2 C．-3 D．2
【详解】解：等式整理得：(x-1)(x+3)=x2+2x-3=x2+mx+n，∴m=2，n=-3则m+n=-1．故选A．
2．已知A，B为多项式，B=2x+1，计算A+B时，某学生把A+B看成A÷B，结果得4x2-2x+1，(1)求出多项式A；(2)求出A+B的正确答案．
【详解】（1）解：依题意得：A=(4x2-2x+1)(2x+1)=8x3-4x2+2x+4x2-2x+1=8x3+1（2）解：A+B=(8x3+1)+(2x+1)=8x3+1+2x+1=8x3+2x+2
知识点三 已知多项式乘积不含某项求字母的值
【分析】根据多项式乘以多项式法则进行运算，再将计算结果中，利用二次项系数为零与一次项的系数为的要求建立方程组，即可求解．
1．已知(x2+mx+1)(x-n)的展开式中不含x项，x2项的系数为-2，求mn+m-n的值．
【详解】解：(x2+mx+1)(x-n)=x3-nx2+mx2-mnx+x-n=x3+(-n+m)x2+(-mn+1)x-n∵展开式中不含x项，x2项的系数为-2，∴-mn+1=0，-n+m=-2，整理得：mn=1，m-n=-2∴mn+m-n=1-2=-1
1．若等式(x+4)(x-5)=x2-mx+n恒成立，则m+n=（　　）A．20 B．21 C．-19 D．-20
【详解】解：(x+4)(x-5)=x2-x-20，∵等式(x+4)(x-5)=x2-mx+n恒成立，∴-m=-1，n=-20，即m=1，n=-20，∴m+n=1-20=-19．故选：C．
2．代数式3a(a2+ab)-6a3b+5a2+3ab(2a2-a)的值（    ）A．与字母a，b都有关B．只与a有关C．只与b有关D．与字母a，b都无关
【详解】解：3a(a2+ab)-6a3b+5a2+3ab(2a2-a)=3a3+3a2b-6a3b+5a2+6a3b-3a2b=3a3+5a2∴代数式3a(a2+ab)-6a3b+5a2+3ab(2a2-a)的值只与a有关，故选：B．
3．已知(-x)(2x2-ax-1)-2x3+3x2中不含x的二次项，则a=__．
【详解】解：∵(-x)(2x2-ax-1)-2x3+3x2中不含x的二次项，∴-2x3+ax2+x-2x3+3x2中，a+3=0，解得：a=-3．故答案为：-3．
4．有若干张如图所示的正方形和长方形卡片，如果要拼一个长为(2a+b)，宽为(a+3b)的矩形．则需要A类卡片_________张，B类卡片_________张，C类卡片_________张．
【详解】解：长为2a+b，宽为a+3b的矩形面积为：(2a+b)(a+3b)=2a2+7ab+3b2，∵A类卡片的面积为a2，B类卡片的面积为b2，C类卡片的面积为ab，∴需要A类卡片2张，B类卡片3张，C类卡片7张．故答案为：2；3；7．
5．甲、乙两人共同计算一道整式乘法题：(3x+a)(2x+b)．甲由于把第一个多项式中的“+a”看成了“-a”，得到的结果为6x2-13x+6；乙由于漏抄了第二个多项式中x的系数，得到的结果为3x2-7x-6．(1)求正确的a、b的值．(2)计算这道乘法题的正确结果．
【详解】（1）解：∵甲由于把第一个多项式中的“+a”看成了“-a”，得到的结果为6x2-13x+6(3x+a)(2x+b)=6x2+(3b-2a)x-ab=6x2-13x+6．∵乙由于漏抄了第二个多项式中x的系数，得到的结果为3x2-7x-6．(3x+a)(2x+b)=3x2+(3b+a)x+ab=3x2-7x-6．∴3b-2a=-13,3b+a=-7∴a=2,b=-3（2）解：(3x+2)(2x-3)=6x2-5x-6．
1、单项式乘多项式，实际上可转化为单项式乘单项式
（1）计算时,要注意符号问题,多项式中每一项都包括它前面的符号,单项式分别与多项式的每一项相乘时，同号相乘得正，异号相乘得负（2）不要出现漏乘现象 （3）运算要有顺序：先乘方，再乘除，最后加减（4）对于混合运算，注意最后应合并同类项
2、多项式乘多项式：多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加