沪科版数学九年级下册24.2《圆的基本性质》（ 第3课时）课件+教案

这是一份沪科版数学九年级下册24.2《圆的基本性质》（ 第3课时）课件+教案，文件包含沪科版数学九年级下册242《圆的基本性质》第3课时课件pptx、沪科版数学九年级下册242《圆的基本性质》第3课时教案docx等2份课件配套教学资源，其中PPT共25页， 欢迎下载使用。

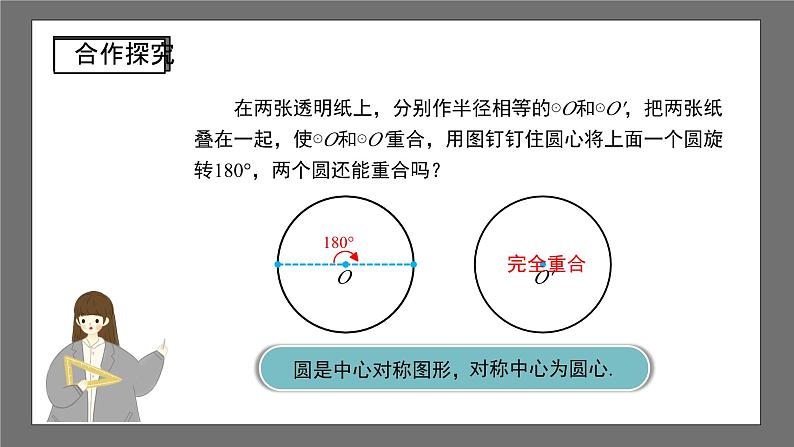
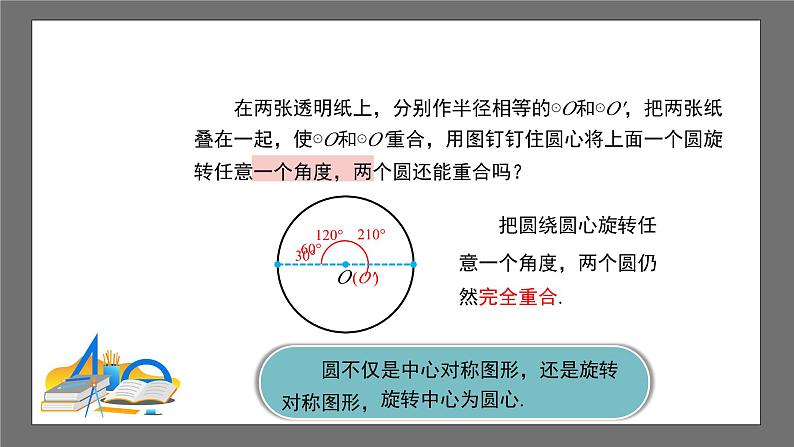
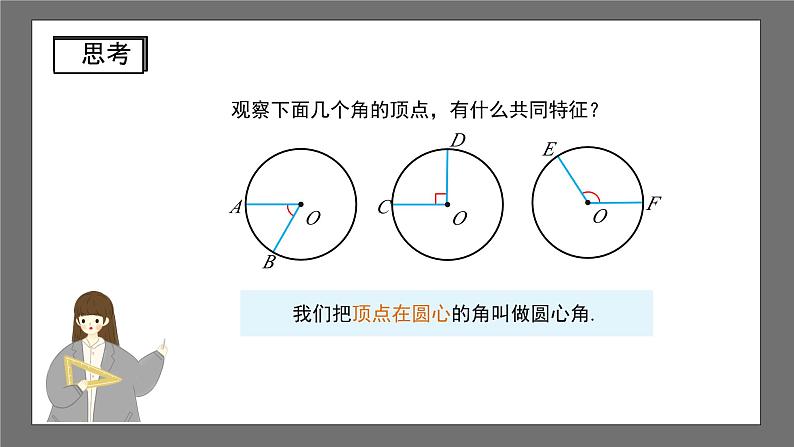
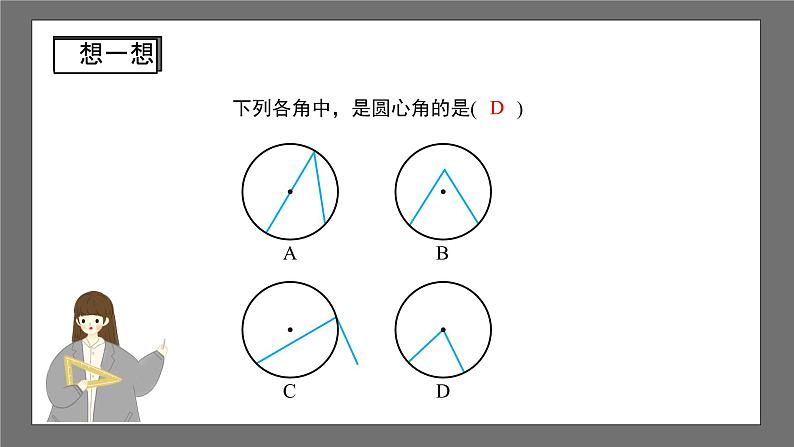
沪科版数学九年级下册24.2 圆的基本性质第4课时 1.理解圆心角的概念和圆的旋转不变性，会辨析圆心角； 2.掌握在同圆或等圆中，圆心角与其所对的弧、弦、弦心距之间的关系，并能运用此关系进行相关的证明和计算； 3.在探索圆心角、弧、弦、弦心距的关系的过程中，学会运用转化的数学思想解决问题； 4.通过观察、比较、操作、推理、归纳等活动，发展空间观念、推理能力等.①圆是轴对称图形，②任何一条直径所在的直线都是圆的对称轴. 在两张透明纸上，分别作半径相等的⊙O和⊙O'，把两张纸叠在一起，使⊙O和⊙O'重合，用图钉钉住圆心将上面一个圆旋转180°，两个圆还能重合吗？O'对称中心为圆心.圆是中心对称图形，完全重合180° 在两张透明纸上，分别作半径相等的⊙O和⊙O'，把两张纸叠在一起，使⊙O和⊙O'重合，用图钉钉住圆心将上面一个圆旋转任意一个角度，两个圆还能重合吗？(O')30°60°120°210°旋转中心为圆心. 圆不仅是中心对称图形，还是旋转对称图形， 把圆绕圆心旋转任意一个角度，两个圆仍然完全重合.观察下面几个角的顶点，有什么共同特征？下列各角中，是圆心角的是( )D ∵AOBA'OB'， ∴BOB'A'OB'A'OB， AOBA'OBα. ∴线段OB与线段OB'重合.又∵OAOA'， OBOB'， ∴旋转后点A与点A'重合，点B与点B'重合.解：根据圆的旋转对称性，把AOB连同 绕圆心O旋转，使线段OA与OA'重合，设A'OAa.A'B'ABMM'α 与 重合；AB与A'B'重合；弦心距OM与OM'重合.点A与点A'重合；点B与点B'重合 在同圆中，相等的圆心角所对的弧相等，所对的弦相等，所对弦的弦心距相等.在等圆中，上述结论是否仍成立？ 在等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对弦的弦心距相等. 定理 在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对弦的弦心距相等.∠AOB∠A'OB' “在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对弦的弦心距相等.”可否把“在同圆或等圆中”去掉？AB=A'B'∠AOB∠A'OB'OM=OM'M'M相等相等相等圆心角、弧、弦、弦心距之间的关系 在同圆或等圆中，如果两个圆心角以及这两个角所对的弧、所对的弦、所对弦的弦心距中，有一组量相等，那么其余各组量都分别相等.圆心角相等弧相等弦相等弦心距相等例1：如图，等边三角形 ABC 的三个顶点都在☉O上. 求证：AOBBOCCOA120°.ABCO证明：连接OA，OB，OC. ∵ABBCCA， ∴AOBBOCCOA  360°120°. 例2：已知：如图，点O是∠FAD平分线上的一点，☉O分别交∠FAD的两边于点C，D和点E，F. 求证：CD=EF.证明：过点O作OKCD，OK'EF，垂足分别为K，K'. ∵OKOK'，(角平分线性质) ∴CDEF.OADEFC 例3：如图，AB，CD是☉O的两条直径，CE为☉O的弦，且CE//AB， 为40°，求BOD的度数. OCEBAD 把顶点在圆心的周角等分360份，每一份的圆心角是1°.1°的圆心角所对的弧就是1°的弧. 一般地，n°的圆心角对着n°的弧， n°的弧对着n°的圆心角.也就是说，圆心角的度数和它所对的弧的度数相等. 例3：如图，AB，CD是☉O的两条直径，CE为☉O的弦，且CE//AB， 为40°，求BOD的度数. OCEBAD解：连接OE. ∵ 为40°， ∴COE40°， ∵OCOE， ∴C 70°. ∵CE//AB， ∴AODC70°. ∴BOD180°70°110°.1. 如果两个圆心角相等，那么( ) A．这两个圆心角所对的弦相等 B．这两个圆心角所对的弧相等 C．这两个圆心角所对的弦的弦心距相等 D．以上说法都不对D2.如图，在☉O中，ABAC，B70°，则A____．40°3.弦长等于半径的弦所对的圆心角等于 . 60°第2题图第3题图 4.圆的一条弦把圆周分成度数比为1  2的两条弧，如果该圆的半径为5，求这条弦的弦长及劣弧所对的圆心角.解：由题意知：劣弧 的度数为120°. 即AOB120°； 过点O做OCAB于点C， ∴AOC AOB60°. 在Rt△AOC中，sinAOC  . ∴AC  . 又∵AB2AC， ∴AB  .C (★拓展)5.在☉O中，2AOBCOD，那么  成立吗？CD2AB呢？如成立，请说明理由；如不成立，那它们之间的关系又是什么？解：  成立，CD2AB 不成立.理由如下： 取 的中点E，连接OE，CE，DE ， 易得AOBCOEDOE， 所以   ，从而  . ABCEDE， 在△CDE中，CE+DECD， 即CD2AB.ABCDEO 推论 在同圆或等圆中，如果两个圆心角以及这两个角所对的弧、所对的弦、所对弦的弦心距中，有一组量相等，那么其余各组量都分别相等.教科书第25页练习第6、7题课程结束