沪科版九年级下册25.2.2 由三视图确定几何体及计算优秀课件ppt

这是一份沪科版九年级下册25.2.2 由三视图确定几何体及计算优秀课件ppt，文件包含沪科版数学九年级下册252《三视图》第2课时课件pptx、沪科版数学九年级下册252《三视图》第2课时教案doc等2份课件配套教学资源，其中PPT共21页， 欢迎下载使用。

能够根据三视图正确想象出立体图形，并总结一定的方法技巧能够建立起三视图与几何体的联系，总结出柱体、椎体等几何体的特征；充分体会由平面图形想象出立体图形的过程，发展学生的空间想象能力；4. 通过由“平面图形”转化为“立体图形”的过程，总结方法与技巧，进一步发展学生解决问题、分析问题的能力，并且培养学生的应用意识.
前面我们已经学习了如何画几何体的主视图、俯视图和左视图，对于下面常见的几何体的三视图，你能准确画出吗？想一想它们的俯视图都是什么图形呢？
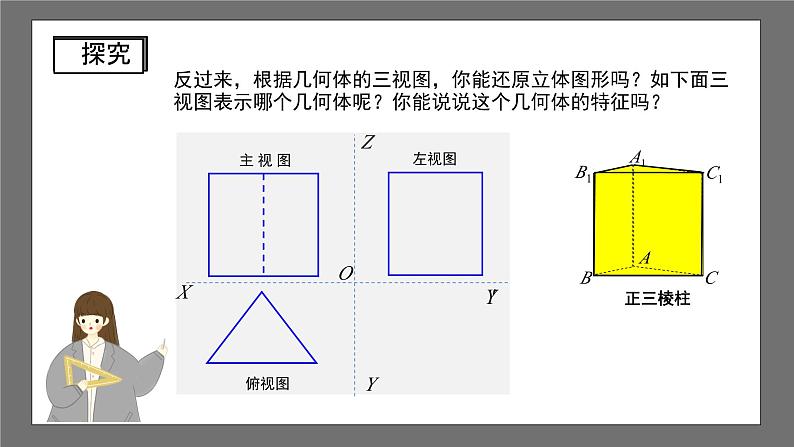
反过来，根据几何体的三视图，你能还原立体图形吗？如下面三视图表示哪个几何体呢？你能说说这个几何体的特征吗？
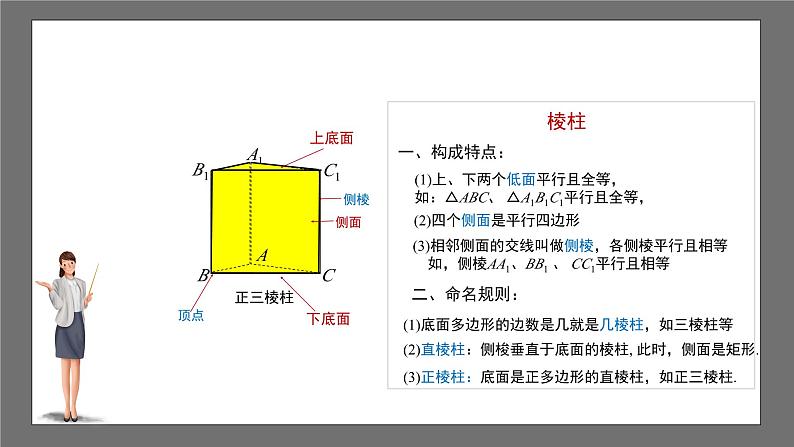
(1)底面多边形的边数是几就是几棱柱，如三棱柱等
(2)四个侧面是平行四边形
(1)上、下两个低面平行且全等，如：△ABC、 △A1B1C1平行且全等，
(3)正棱柱：底面是正多边形的直棱柱，如正三棱柱.
(2)直棱柱：侧梭垂直于底面的棱柱, 此时，侧面是矩形.
(3)相邻侧面的交线叫做侧棱，各侧棱平行且相等 如，侧棱AA1、BB1 、 CC1平行且相等
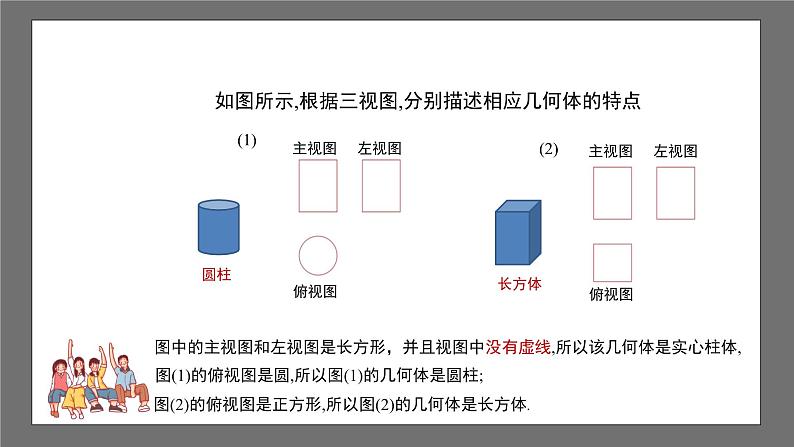
图中的主视图和左视图是长方形，并且视图中没有虚线,所以该几何体是实心柱体,
图(2)的俯视图是正方形,所以图(2)的几何体是长方体.
图(1)的俯视图是圆,所以图(1)的几何体是圆柱;
如图所示,根据三视图,分别描述相应几何体的特点
(2)左视图：反映几何体从左到右的形状轮廓， 显示几何体的高度和宽度.
(3)俯视图：反映几何体从上到下的形状轮廓， 显示几何体的长度和宽度.
几何体是( )
几何体是( )
根据三视图，写出对应的几何体
例1.如图，分别根据三视图(1)(2) 说出几何体的名称．
解：(1)从正面、侧面看几何体，视图都是等腰三角形， 说明这个几何体是锥体， 再结合俯视图是正方形，可以想象几何体是四棱锥， 因主视图中间没有实线，所有摆放位置如图所示：
(2)从正面、侧面看几何体，视图都是等腰三角形, 说明实物是锥体， 从上面看，俯视图是圆形，说明这个几何体是圆锥，如图所示．
解：组合体是大小不同的两个长方体上下组合而成.
例2.下图是一个组合体的三视图,这个组合体是由什么样的几何体组成的?
例3. 根据物体的三视图，描述物体的形状．
分析：主视图显示物体正面是正五边形，由俯视图可知，由上向下看到物体有两个面是矩形，中间的实线表示相交于一条棱虚线表示另有两条棱被遮挡.
解：物体是正五棱柱形状的，如图所示．
例4．由一些大小相同的小正方体组成的简单几何体的主视图和俯视图,如图所示．(1)请你画出这个几何体的左视图；(2)若组成这个几何体的小正方体的块数为n，请你写出n的所有可能值．
分析： (1)依据“高平齐，宽相等”确定左视图的宽是2个小正方形宽，高是三个小正方形高，所以有5种情形(2)根据俯视图，数出每一个小正方形上小方块的个数即可
(2)n=8，9，10，11．
解： (1)左视图有以下5种情形，如图所示
1．一个物体的俯视图是圆，则该物体的形状是（ ）．A．球体 B．圆柱 C．圆锥 D．以上都有可能2．一个几何体的三视图如图所示，则这个几何体是（ ）．
A．圆柱 B．圆锥 C．长方体 D．正方体
3．如图是某几何体的三视图，则该几何体是下图中的（ ）．
(1)主视图：反映几何体从前到后的形状轮廓，显示几何体的高度和长度(2)左视图：反映几何体从左到右的形状轮廓，显示几何体的高度和宽度.(3)俯视图：反映几何体从上到下的形状轮廓，显示几何体的长度和宽度. 将三者结合起来想象出几何体