沪科版八年级下册17.1 一元二次方程优秀ppt课件

这是一份沪科版八年级下册17.1 一元二次方程优秀ppt课件，文件包含173《一元二次方程根的判别式》课件pptx、沪科版数学八年级下册173《一元二次方程根的判别式》教案docx等2份课件配套教学资源，其中PPT共17页， 欢迎下载使用。

（1）熟练掌握运用一元二次方程根的判别式判别方程是否有根及两根是否相等；（2）理解为什么能用根的判别式判别一元二次方程根的情况；（3）经历一元二次方程根的判别式的探究过程，体会分类讨论和转化的思想方法，感受数学思想严密性及方法的灵活性；（4）通过探索一元二次方程根的判别式与根个数关系，使学生感受到数学知识间的联系，提升数学的学习兴趣.
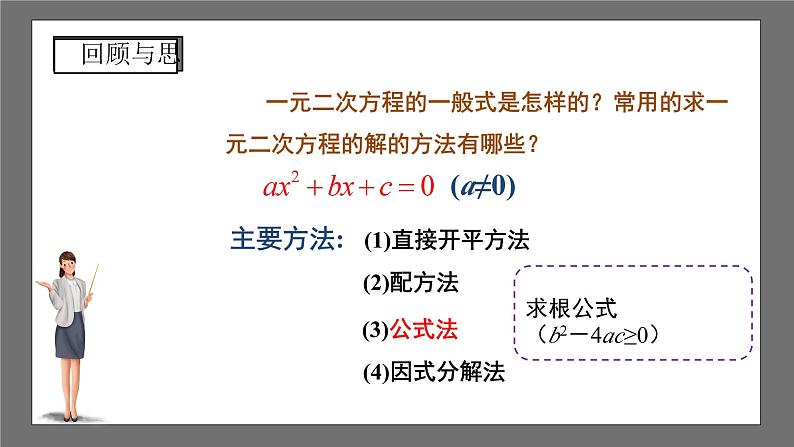
一元二次方程的一般式是怎样的？常用的求一元二次方程的解的方法有哪些？
主要方法: (1)直接开平方法 (2)配方法 (3)公式法 (4)因式分解法
用配方法解方程 ax2 + bx +c = 0(a≠0) .
问题2：什么情况下可以直接开平方？什么情况下不能直接开？
(3)当 b2 – 4ac ＜0 时，
方程有两个不相等的实数根.
(1)当 b2– 4ac＞0 时，
(2)当 b2– 4ac=0 时，
方程有两个相等的实数根.
方程没有实数根.
根的个数b2-4ac决定
不解方程，判别下列方程根的情况：
(1)5x2−3x − 2＝0；
(2)25y2+4＝20y；
解： (1)因为∆＝(− 3)2 − 4×5×(− 2)＝49＞0，
所以原方程有两个不相等的实数根.
因为∆＝(− 20)2 − 4×25×4＝0，
所以原方程有两个相等的实数根.
所以原方程没有实数根.
1.不解方程，判别下列方程根的情况：
解：(1)因为∆ =(− 5)2 − 4×2×(− 4)=57＞0，
解：(2)因为∆=(− 5)2 − 4×7×2= − 31＜0，
解：(3)原方程可变形为x2+x − 3=0，
因为∆=12 − 4×1×(− 3)=13＞0，
2. 已知关于x的方程x2 − 3x＋k＝0，问k取何值时，这个方程： (1)有两个不相等的实数根？ (2)有两个相等的实数根？ (3)没有实数根？
解：因为 ∆=(− 3)2 − 4×1×k=9 − 4k，
一元二次方程根的判别式
教科书：第36页习题17.3第1、2、4题.