沪科版八年级下册19.2 平行四边形优质课件ppt

这是一份沪科版八年级下册19.2 平行四边形优质课件ppt，文件包含沪科版数学八年级下册192《平行四边形的判定》第1课时课件pptx、沪科版数学八年级下册192《平行四边形的判定》第1课时教案docx等2份课件配套教学资源，其中PPT共22页， 欢迎下载使用。
1. 通过平移与作图探索并掌握判别四边形是平行四边形的条件.2.能运用平行四边形的性质定理和判定定理进行证明和计算.3.经历平行四边形判定定理的探索过程，发展合情推理的意识和表述能力，体会几何思维的真正内涵.4.经历平行四边形的判定定理的探索过程，培养协作、探究精神.
前面我们学习了平行四边形的定义和性质，你能说出它的具体内容吗？
两组对边分别平行的四边形叫平行四边形.
平行四边形的对角线互相平分
由以前的经验接下来我们应该研究什么？
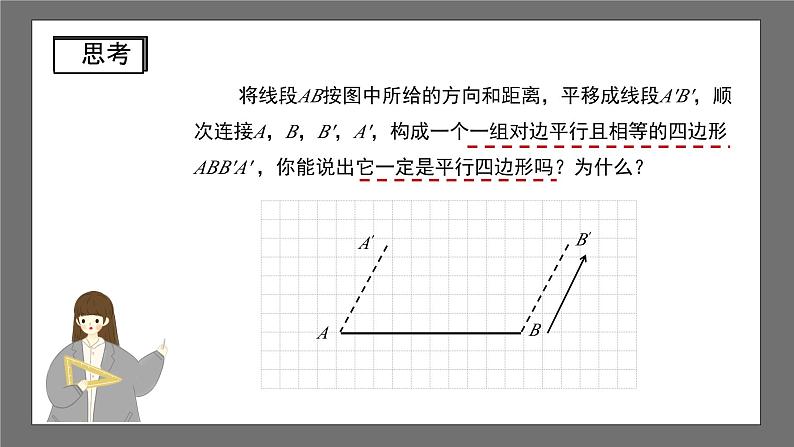
将线段AB按图中所给的方向和距离，平移成线段A′B′，顺次连接A，B，B′，A′，构成一个一组对边平行且相等的四边形ABB′A′ ，你能说出它一定是平行四边形吗？为什么？
已知：如图，在四边形ABCD中， AB//DC，且AB=DC.求证：四边形ABCD是平行四边形.
已知AB∥DC，只要再证明AD∥BC，即可证明所求.
∵ AB∥DC ， ∴∠BAC=∠DCA.
∴ △ABC ≌ △CDA .
又 ∵AB=CD，AC=CA.
∴∠ACB=∠CAD. ∴ AD∥BC .
因此，四边形ABCD是平行四边形.
一组对边平行且相等的四边形是平行四边形.
由此得到判定四边形是否为平行四边形的方法有：
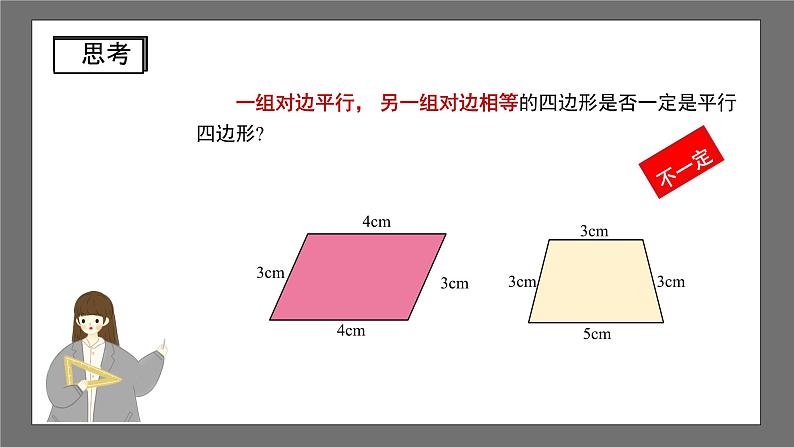
一组对边平行， 另一组对边相等的四边形是否一定是平行四边形?
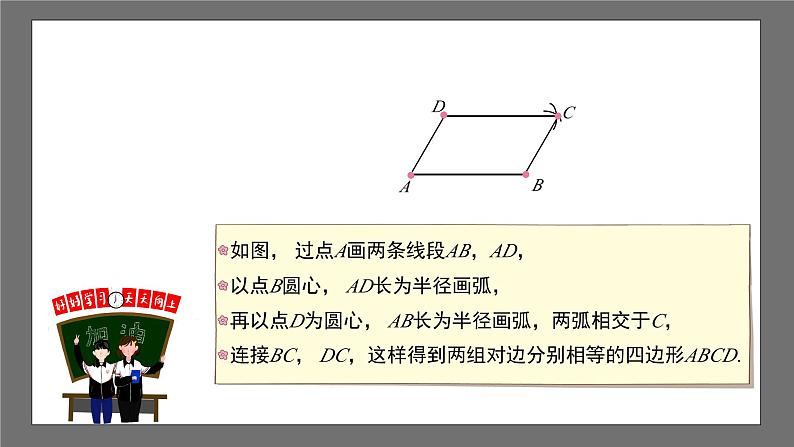
如图， 过点A画两条线段AB，AD，
以点B圆心， AD长为半径画弧，
再以点D为圆心， AB长为半径画弧，两弧相交于C，
连接BC， DC，这样得到两组对边分别相等的四边形ABCD.
这样做出来的四边形是平行四边形吗？为什么？
已知AB=DC， AD＝BC.
已知两组对边分别相等，只要再证明任意一组对边平行，即可证明所画四边形为平行四边形.
∵ AB=DC， AD＝BC，
∴ △ABC ≌ △CDA，∠CAB=∠ACD .
∵ AB=DC， AB∥DC .
两组对边分别相等的四边形是平行四边形.
由此得到判定四边形是否为平行四边形的方法还有：
在四边形ABCD中，∵AB=CD，AD=BC，∴四边形ABCD是平行四边形.
如图， 作两条直线l1， l2相交于点O，
在直线l1上截取OA=OC，在直线l2上截取OB=OD，
连接AB，BC，CD，DA.
这样画出来的四边形ABCD的对角线就互相平分.
已知OA=OC， OB＝OD.
可证明一组对边平行且相等来说明所画四边形为平行四边形.
∵ OA=OC，OB＝OD，
∴ △AOD ≌ △COB.
又 ∵∠AOD=∠COB，
∴ AD=CB，∠DAO=∠BCO .
∴四边形ABCD是平行四边形.
∵ ∠DAO=∠BCO ，∴ AD∥CB .
∵ AD∥CB ，且 AD=CB.
对角线互相平分的四边形是平行四边形.
在四边形ABCD中，∵OA=OC，OB=OD，∴四边形ABCD是平行四边形.
两组对边分别平行的四边形是平行四边形.
∵AB∥CD，AD∥BC，∴四边形ABCD是平行四边形.
∵AB∥CD，AB=CD，(或AD∥BC，且AD=BC)，∴四边形ABCD是平行四边形.
∵AB=CD，且AD=CB，∴四边形ABCD是平行四边形.
∵AO=CO，BO=DO，∴四边形ABCD是平行四边形.
上的线段，故可考虑使用“定理3”.
连接BD交AC于点O.
∵四边形ABCD是平行四边形，
∴AO=CO，BO=DO
∴OE=AOAE=COCF=OF.
∴四边形BEDF是平行四边形.
1. 已知：如图，在四边形ABCD中，∠A=∠C，∠B=∠D.试判断四边形ABCD是否是平行四边形，并说明理由.
∵ ∠A+∠B+∠C+∠D=360°
又 ∵∠A=∠C，∠B=∠D，
∴ 2∠A+2∠B=360°，即∠A+∠B=180°.
∴ AD∥BC ，同理得AB∥CD，
2. 如图，在四边形ABCD中，AB=CD，过点A作AE⊥BD，交BD于点E，过点C作CF⊥BD交BD于点F，且AE=CF.求证：四边形ABCD是平行四边形.
已知AB=CD相等，可证AB∥CD或者AD=CB.
∵AE⊥BD，CF⊥BD，∴∠AEB=∠CFD=90°.
在Rt△ABE和Rt△CDF中，∵AE=CF，AB=CD，
∴Rt△ABE≌Rt△CDF.
∴∠ABE=∠CDF， AB∥CD.
又∵AB=CD，∴四边形ABCD是平行四边形.
3. 四边形的四条边长分别是a，b，c，d，其中a，b为一组对边长，c，d为另一组对边长且a2＋b2＋c2＋d2＝2ab＋2cd，则这个四边形是(　　)
A．任意四边形 B．平行四边形C．对角线相等的四边形 D．对角线垂直的四边形
教科书第85页习题19.2第8题、第9题.