鲁教版 (五四制)六年级下册第七章 相交线与平行线1 两条直线的位置关系优质ppt课件

这是一份鲁教版 (五四制)六年级下册第七章 相交线与平行线1 两条直线的位置关系优质ppt课件，共21页。PPT课件主要包含了回顾知识，或1或2或3，有公共顶点，方向相对，互为反向延长线，对顶角是怎样形成的，据题意可得，同角或等角的余角相等，同角或等角的补角相等，垂线的性质等内容，欢迎下载使用。

1．在同一平面内，两条直线的位置关系可能是( ) A.相交、平行 B.相交、垂直 C.平行、垂直 D.平行、相交、垂直
同一平面内两条直线的位置关系
若两条直线只有一个公共点，我们称这两条直线为相交线。
在同一平面内，不相交的两条直线叫做平行线。
1,三条直线平行,交点数0；2,其中两条平行,交点数2；3,三条直线相交于同一点,交点数1；4,三条直线相交于不同点,交点数3,综合一下,交点个数可能为0,1,2,3.
2.在一个平面内，有三条直线，则交点的个数可能是_______________
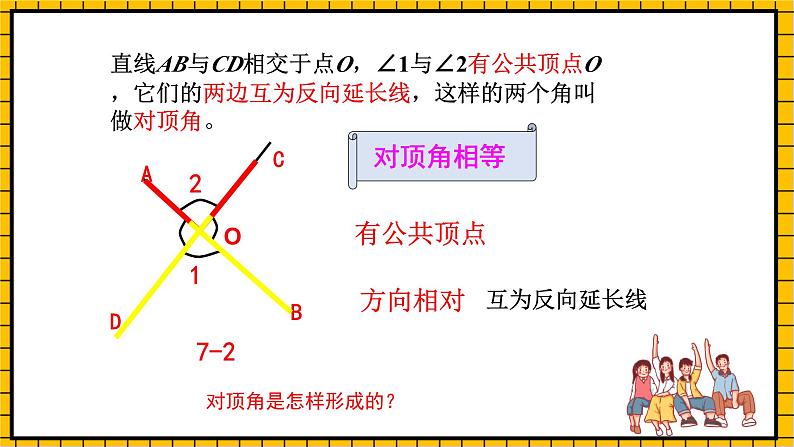
直线AB与CD相交于点O，∠1与∠2有公共顶点O，它们的两边互为反向延长线，这样的两个角叫做对顶角。
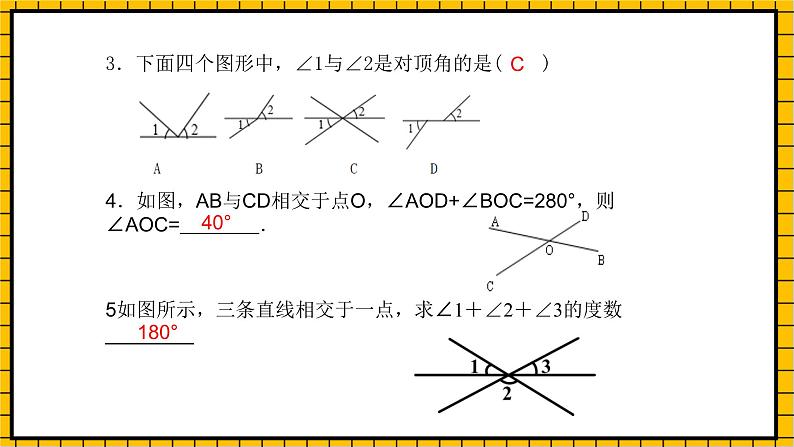
3．下面四个图形中，∠1与∠2是对顶角的是( )
4．如图，AB与CD相交于点O，∠AOD+∠BOC=280°，则∠AOC= ．
5如图所示，三条直线相交于一点，求∠1＋∠2＋∠3的度数________
如果两个角的和是180°，那么称这两个角互为补角。或称这两个角互补，其中一个角是另一个角的补角。
如果两个角的和是90°，那么称这两个角互为余角。或称这两个角互余，其中一个角是另一个角的余角。
两个角有一条公共边,它们的另一条边互为反向延长线。具有这种关系的两个角,互为邻补角。图中,∠AOC有两个邻补角:∠AOD和∠BOC。(注:补角只注重数量关系两角之和是180°,无论是否有公共边均可,但邻补角还要注重位置上的关系)。
6．已知∠1与∠2是对顶角，∠2与∠3是邻补角，则∠1+∠3=_______．
7．已知∠β为∠α的补角，∠γ为∠α的余角，则∠β-∠γ=_______．
一个锐角的补角比这个角的余角大900对吗？因为∠β=180°-∠α，∠γ=90°-∠α所以∠β-∠γ=（180°-∠α)-(90°-∠α)=90°
8．一个角的余角是80°，则这个角补角是_______
9.一个角的补角是它的余角的4倍，则这个角等于___．
解：设这个角为 x, 则这个角的补角为（180°-x）, 则这个角的余角为（90°-x）.根据题意可得：180°-x=4(90°-x)解得：x=60°
10.若一个角的余角与它的补角的和为210°，则这个角的余角等于______．11.若一个角的补角与这个角的余角的度数之比是3：1，则这个角等于————————
解：设这个角余角为 x, 则这个角的补角为90°+ x x+90°+ x=210°
解：设这个角为 x,这个角的补角为（180°-x），这个角的余角为（90°-x）
（180°-x）=3（90°-x）
定义：两条直线相交成四个角，如果有一个角是直角，那么称两条直线互相垂直。其中的一条直线叫做另一条直线的垂线。
平面内，过一点有且只有一条直线与已知直线垂直。
平面内，一条直线的垂线有无数条。
线段PO的长度叫做点P到直线m的距离
直线外一点与直线上各点所连的所有线段中垂线段最短
线段PO叫做点P到直线m的垂线段
分别找出图中互相垂直的线段：
BC ⊥CA BC ⊥DCBC ⊥DA CE ⊥ACCE ⊥DC CE ⊥DA
还有互相垂直的线段吗？
12．如图所示，已知OA⊥OB，OC⊥OD，∠AOC︰∠BOD＝1︰2，则∠BOD＝________．
13.如图所示，AC⊥BC，CD⊥AB，点A到BC边的距离是线段　 　的长，点B到CD边的距离是线段　 　的长，∠A的余角有　 　，和∠B相等的角有　 　．
∠AOC+∠BOD=180°
14．如图，要从小河引水到村庄A，请设计并作出一最短路线，理由是___________________．
15.如图，直线a⊥b，∠1=50°，则∠2=　　度．
解：∵a⊥b，（ ） ∴∠1+∠2+90°=180°（ ， ）∴∠1+∠2=90°，（ ）∵∠1=50°，（ ）∴∠2=90°﹣∠1=40°．
16．如图，直线AB、CD相交于点O，OE⊥CD，OF⊥AB，∠BOD=25°，求∠AOE和∠DOF的度数．
∵OE⊥CD,∴∠COE=_____°(垂线定义)∵∠AOC=∠BOD=25°( )∴∠AOE=∠COE-________=65°∵OF⊥AB,∴∠FOB=______°(垂线定义 )∴∠DOF=∠FOB+________=_____°
17.直线AB、CD相交于O点，若∠DOE=40°，∠BOC=130°，猜想射线OE与直线AB的位置关系，并说明理由．
∵∠BOC=130°,∴∠AOD=∠BOC=130°( )∵∠AOD=∠AOE+______=130°∴∠AOE=∠AOD - _______∵∠DOE=40°,∴∠AOE=_____°
所以射线OE与直线AB互相垂直
18.如图所示，将长方形纸片折叠，使点A落在点A′处，BC为折痕，BD是∠A′BE的平分线，试说明CB与BD的位置关系．
由折叠可得：∵BD是∠A′BE的平分线∴__________________∵∠ABA′+∠A′BE=______°∴∠CBD=∠A′BC+_______ = =90°∴CB⊥BD
如图，点O为直线AB上一点，OC为一射线，OE平分∠AOC，OF平分∠BOC．试探究OE，OF的位置关系.
19．如图甲所示，AO⊥BO,CO⊥DO．（1）试猜想∠AOD与∠COB在数量上是相等，互余，还是互补的关系，你能用推理的方法说明你的猜想是否合理吗？（2）当∠COD绕点O旋转到图乙的位置时，你原来的猜想还成立吗？
∵AO⊥BO,CO⊥DO,∴∠AOB=∠COD=______°∵∠AOD=∠AOB+______ ∠BOC=∠COD -∠BOD ∴∠AOD+∠BOC=(∠AOB+______)+(∠COD -∠BOD)=∠AOB+∠COD=_______°
∴∠AOD与∠BOC互补
1.你学到了哪些知识？2.你学会了哪些方法？3.你认为应注意哪些问题？4.你还有哪些困惑？