数学九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数课文内容课件ppt

这是一份数学九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数课文内容课件ppt，共60页。PPT课件主要包含了二次函数的定义，温馨提示，直线xh，k＞0，y2x2+2x+1，y2x2+x+2，y-8x2-12x，yx2-1，yx-52+2，y-2x+32等内容，欢迎下载使用。
1.梳理本章的知识要点，回顾与复习本章知识.2.进一步巩固二次函数的概念、图象和性质，能熟练应用二次函数的图象和性质解决有关问题.（重点）3.能应用二次函数与一元二次方程之间的关系解决函数与方程的问题，会用待定系数法求二次函数解析式.4.熟练应用二次函数的有关知识解决实际问题，体会其中的建模思想.（难点）
形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数.其中x是自变量，a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
（1）等号左边是变量y，右边是关于自变量x的整式，a,b,c为常数，且a≠0;（2）等式的右边最高次数为2，可以没有一次项和常数项，但不能没有二次项； （3）一般情况下，自变量x的取值范围是任意实数.
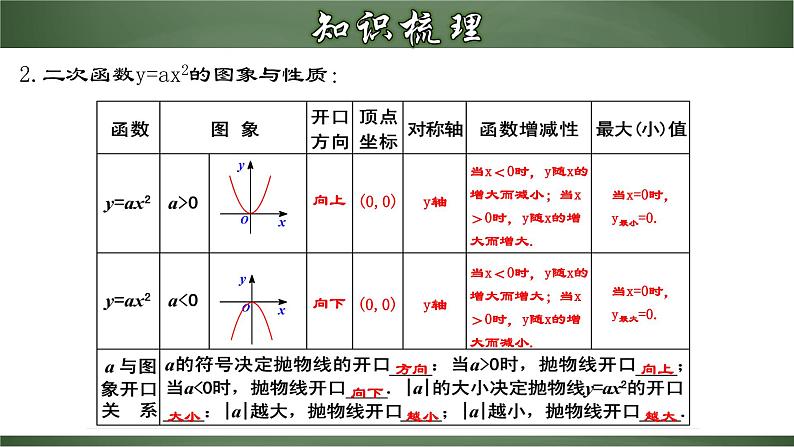
当x＜0时，y随x的增大而减小；当x＞0时，y随x的增大而增大.
当x＜0时，y随x的增大而增大；当x＞0时，y随x的增大而减小.
当x=0时，y最小=0.
当x=0时，y最大=0.
2.二次函数y=ax2的图象与性质：
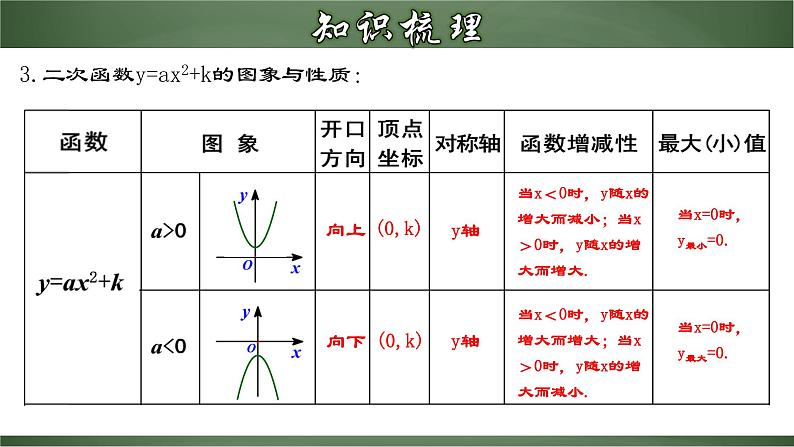
3.二次函数y=ax2+k的图象与性质：
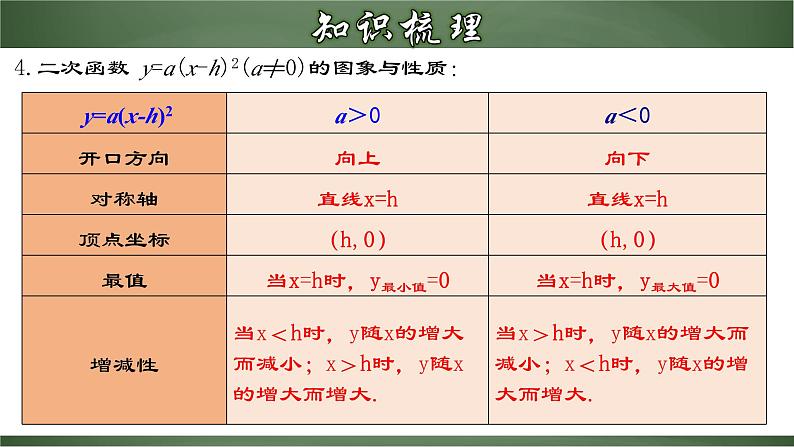
4.二次函数 y=a(x-h)2(a≠0)的图象与性质：
5.二次函数 y=a(x-h)2+k(a≠0)的图象与性质：
一般地，抛物线y=a(x-h)2+k与y=ax2形状相同，位置不同.把抛物线y=ax2向上(下)向左(右)平移，可以得到抛物线y=a(x-h)2+k.平移的方向、距离要根据h、k的值来决定.
6.二次函数图象平移规律：
7.二次函数y=ax2+bx+c的性质：
8.二次函数y=ax2+bx+c的图象与a、b、c的关系：
9.二次函数解析式的类型及适用情况：
(1)如果抛物线y=ax2+bx+c与x轴有公共点，公共点的横坐标是x0，那么当x=x0时，函数的值是0，因此x=x0就是方程ax2+bx+c=0的一个根.
(2)二次函数y=ax2+bx+c的图象与x轴的位置关系有三种：没有公共点，有一个公共点，有两个公共点.这对应着一元二次方程ax2+bx+c=0的根的三种情况：没有实数根，有两个相等的实数根，有两个不等的实数根.
10.二次函数与一元二次方程的关系：
(1)二次函数解决几何面积最值问题的方法
1.求出函数解析式和自变量的取值范围；2.配方变形，或利用公式求它的最大值或最小值,3.检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
11.利用二次函数解决典型实际问题：
(2)求解最大利润问题的一般步骤
1.建立利润与价格之间的函数关系式：运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
2.结合实际意义，确定自变量的取值范围；
3.在自变量的取值范围内确定最大利润：可以利用配方法或公式求出最大利润；也可以画出函数的简图，利用简图和性质求出.
(3)在“拱桥类”问题中，一般知道拱高和拱长，这时可根据抛物线的对称性建立以对称轴为y轴的坐标系，然后根据所建立的坐标系，确定抛物线上一些点的坐标.若顶点在原点上，一般设二次函数的解析式为y=ax2；若顶点不在原点上，一般设二次函数的解析式为y=ax2+k.步骤：(1)恰当地建立直角坐标系；(2)将已知条件转化为点的坐标；(3)合理地设出所求函数关系式；(4)代入已知条件或点的坐标求出关系式；(5)利用关系式求解问题.
例1.下列函数一定是二次函数的是__________．① y=ax2+bx+c ；② ；③ y=4x2-3x+1；④ y=(m-1)x2-bx+c ；⑤ y=(x-3)2-x2
解：①y=ax2+bx+c，必须满足a≠0才为二次函数，故①不一定是二次函数；②等号右边为分式，故②不是二次函数；③y=4x2-3x+1是二次函数，故③是二次函数；④y=(m-1)x2-bx+c，m=1时，该式不是二次函数；⑤y=(x-3)2-x2=x2-6x+9-x2=-6x+9，该式不是二次函数；
【点睛】判断一个函数是不是二次函数，先看原函数和整理化简后的形式再作判断.除此之外，二次函数除有一般形式y=ax2+bx+c(a≠0)外，还有其特殊形式如y=ax2,y=ax2+bx, y=ax2+c等.
解：(1)∵这个函数是二次函数，∴m2－m≠0，∴m(m－1)≠0，∴m≠0且m≠1.(2)∵这个函数是一次函数，∴ ∴m＝0.
例2.已知函数y＝(m2－m)x2＋(m－1)x＋2－2m.(1)若这个函数是二次函数，求m的取值范围．(2)若这个函数是一次函数，求m的值．(3)这个函数可能是正比例函数吗？为什么？
(3)不可能．∵当m＝0时，y＝－x＋2，∴不可能是正比例函数．
【1-2】已知y=（m+2）x|m|+2是关于x的二次函数，那么m的值为（　　）A．-2 B．2 C．±2 D．0
【1-1】已知函数：①y=2x-1；②y=-2x2-1；③y=3x3-2x2；④y=2x2-x-1；⑤y=ax2+bx+c，其中二次函数的个数为（　　）A．1 B．2 C．3 D．4
【1-3】把下列二次函数化成一般形式，并指出二次项系数、一次项系数及常数项.
【分析】∵二次函数的解析式为： ，∴该二次函数的对称轴为：直线x=2，∴点 关于对称轴的对称点 为(0,y3)，∵点A,B, 都在对称轴左侧，对称轴左侧随的增大而增大∴ y1＜y3＜y2
例4.已知二次函数y＝a(x－1)2－c的图象如图所示，则一次函数y＝ax＋c的大致图象可能是(　　)
【分析】根据二次函数开口向上则a＞0，根据－c是二次函数顶点坐标的纵坐标，得出c＞0，故一次函数y＝ax＋c的大致图象经过第一、二、三象限．故选A.
例5.已知二次函数y=－x2＋2bx＋c，当x＞1时，y的值随x值的增大而减小，则实数b的取值范围是（ ）A．b≥－1 B．b≤－1 C．b≥1 D．b≤1
【2-1】下列关于二次函数y＝2x2的说法正确的是（ ）A．它的图象经过点（－1，－2）B．它的图象的对称轴是直线x＝2C．当x＜0时，y随x的增大而增大D．当－1≤x≤2时，y有最大值为8，最小值为0
【2-2】已知二次函数 ，下列说法正确的是（       ）A．图象开口向上 B．图象的顶点坐标为(-2,3)C．图象的对称轴是直线x=-3 D．有最大值，为－3
【2-3】已知二次函数y=2(x-3)2+1，下列说法:①其图象开口向下;②其图象的对称轴为直线x=-3;③当x=3时，函数有最大值1;④当x