第二十三章旋转 单元复习课件

这是一份第二十三章旋转 单元复习课件，共29页。

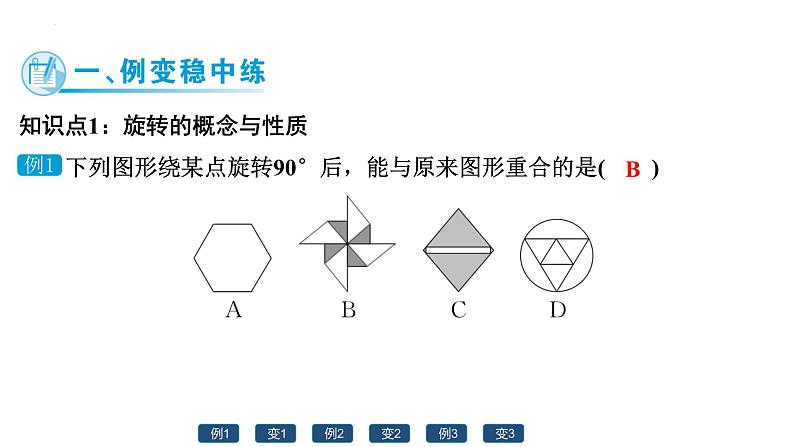
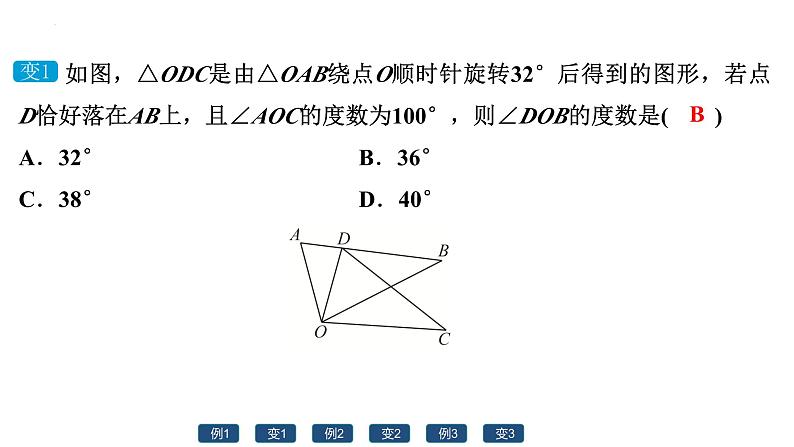
第二十三章旋转 单元复习 01 例变稳中练 例1 变1 例2 变2 例3 变3 知识点1：旋转的概念与性质　　下列图形绕某点旋转90°后，能与原来图形重合的是(　　) 返回目录 例变稳中练 例1 变1 例2 变2 例3 变3 B　　如图，△ODC是由△OAB绕点O顺时针旋转32°后得到的图形，若点D恰好落在AB上，且∠AOC的度数为100°，则∠DOB的度数是(　　)A．32° B．36°C．38°　 D．40° 返回目录 例变稳中练 例1 变1 例2 变2 例3 变3 B知识点2：中心对称与中心对称图形　　如图，以某网格线所在直线建立平面直角坐标系，将△ABC绕点P旋转180°得到△DEF，已知点A(2，－1)，点P的坐标为(　　)A．(－2，2)　 B．(2，－2)C．(1，－3) D．(－3，1) 返回目录 例变稳中练 例1 变1 例2 变2 例3 变3 C　　下列图形中，是中心对称图形而不是轴对称图形的是(　　) 返回目录 例变稳中练 例1 变1 例2 变2 例3 变3 C知识点3：旋转作图　　(2022秋·安徽期末)如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均为格点(网格线的交点)．(1)请画出△ABC绕点O逆时针方向旋转90°后得到的图形△A1B1C1.(点A，B，C的对应点分别为点A1，B1，C1)解：如答图，△A1B1C1为所作． 返回目录 例变稳中练 例1 变1 例2 变2 例3 变3 　　(2022秋·安徽期末)如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均为格点(网格线的交点)．(2)请画出(1)中△A1B1C1关于原点O对称的图形△A2B2C2.(点A1，B1，C1的对应点分别为点A2，B2，C2)解：如答图，△A2B2C2为所作． 返回目录 例变稳中练 例1 变1 例2 变2 例3 变3 　　(2022秋·苍溪县期末)如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A(－3，5)，B(－2，1)，C(－1，3)．(1)若△ABC和△A1B1C1关于原点O成中心对称图形，写出△A1B1C1的各点的坐标；解：如答图，△A1B1C1即为所求．A1 (3，－5)，B1 (2，－1)，C1 (1，－3)． 返回目录 例变稳中练 例1 变1 例2 变2 例3 变3 　　(2022秋·苍溪县期末)如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A(－3，5)，B(－2，1)，C(－1，3)．(2)将△ABC绕着点O顺时针方向旋转90°得到△A2B2C2，画出图形并写出△A2B2C2的各点的坐标．解：如答图，△A2B2C2即为所求．A2 (5，3)，B2 (1，2)，C2 (3，1)． 返回目录 例变稳中练 例1 变1 例2 变2 例3 变3 02 四基三级练 1 2 5 一级 二级 三级 3 4 一级1．下列图案中，属于中心对称图形的是(　　) 返回目录 1 2 5 3 4 四基三级练C2．若点P(x，y)在第四象限内，且|x|＝3，|y|＝5，则点P关于原点对称点的坐标是(　　)A．(－3，－5) B．(5，－3)C．(－5，3) D．(－3，5) 返回目录 四基三级练 1 2 5 3 4 D二级3．如图，将△ABC绕点A逆时针旋转到△ADE的位置，B，D，C在一条直线上．若∠B＝70°，则∠CAE的大小为____. 返回目录 四基三级练 1 2 5 3 4 40°4．如图，在Rt△ABC中，∠ACB＝90°，∠A＝60°，AC＝1，将△ABC绕点C按逆时针方向旋转得到△A′B′C，此时点A′恰好在AB边上，连接BB′，则△A′BB′的周长为(　　) 返回目录 四基三级练 1 2 5 3 4 D三级5．如图，在△ABC中，AB＝AC＝1，∠BAC＝45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE，CF相交于点D.(1)求证：CF＝BE；证明：∵△AEF是由△ABC绕点A按顺时针方向旋转得到的，∴AE＝AB＝AF＝AC＝1，∠EAF＝∠BAC，∴∠EAF＋∠BAF＝∠BAC＋∠BAF， △ABE，∴CF＝BE. 返回目录 四基三级练 1 2 5 3 4 (2)当四边形ACDE为菱形时，求BD的长． 返回目录 四基三级练解：∵四边形ACDE为菱形，AB＝AC＝1，∴DE＝AE＝AC＝AB＝1，AC∥DE，∴∠AEB＝∠ABE，∠ABE＝∠BAC＝45°，∴∠AEB＝∠ABE＝45°，∴△ABE为等腰直角三角形， 1 2 5 3 4 03 思维拓展6．(2022秋·罗湖区校级期末)如图，点E为正方形ABCD内一点， ∠AEB＝90°，将Rt△AEB绕点B按顺时针方向旋转90°，得到△CE′B(点A的对应点为点C)，连接DE，延长AE交CE′于点F，则四边形BE′FE为正方形，若AB＝15，CF＝3，则DE的长为_______.思维拓展 返回目录 课后强化1．下列图形中，既是轴对称图形又是中心对称图形的有(　　) 返回首页 1 2 5 6 3 4 7 8D2．如图是华为手机图库标志，这个图案绕着它的中心旋转一定角度后与自身重合，这个旋转角至少为(　　)A．30° B．45°C．60° D．90° 返回首页 1 2 5 6 3 4 7 8C3．(－3，4)关于x轴对称的点的坐标为____________，关于y轴对称的点的坐标为________，关于原点对称的坐标为__________． 返回首页 1 2 5 6 3 4 7 8(－3，－4)(3，4)(3，－4)4．如图，将△ABC绕点C顺时针旋转得到△EDC，若点A恰好在ED的延长线上，∠BAC＝40°，则∠BAE的度数为(　　)A．80° B．60°C．65° D．70° 返回首页 1 2 5 6 3 4 7 8A5．如图，在矩形ABCD中，AD＝2，将矩形ABCD绕点A逆时针旋转，得到矩形AEFG，点B的对应点E落在CD上，且DE＝EF，则四边形ABCE的面积为(　　) 返回首页 1 2 5 6 3 4 7 8C6．如图，在等边△ABC中，AB＝6，点D是BC的中点，将△ABD绕点A逆时针旋转后得到△ACE，那么线段DE的长为(　　) 返回首页 1 2 5 6 3 4 7 8C7．在如图的方格纸中，每个小方格都是边长为1个单位长度的正方形，△ABC的顶点均在格点上，请在所给的平面直角坐标系中按要求画图：(1)作△ABC关于坐标原点成中心对称的△A1B1C1；解：如答图所示，△A1B1C1即为所求； 返回首页 1 2 5 6 3 4 7 87．在如图的方格纸中，每个小方格都是边长为1个单位长度的正方形，△ABC的顶点均在格点上，请在所给的平面直角坐标系中按要求画图：(2)作△ABC绕点O顺时针旋转90°得到的△A2B2C2. 返回首页 解：如答图所示，△A2B2C2即为所求． 1 2 5 6 3 4 7 88．如图，将△ABC纸片绕点C顺时针旋转40°得到△A′B′C，连接AA′，若AC⊥A′B′，则∠AA′B′的度数为(　　)A．20° B．40°C．50° D．60° 返回首页 1 2 5 6 3 4 7 8A