南阳市第一中学校2023-2024学年高一下学期5月月考数学试卷(含答案)

这是一份南阳市第一中学校2023-2024学年高一下学期5月月考数学试卷(含答案)，共15页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1．如果点位于第四象限,那么角所在的象限是( )
A.第一象限B.第二象限C.第三象限D.第四象限
2．若，则( )
A.B.1C.2D.4
3．已知,则( )
A.B.C.D.
4．已知是单位向量,,则向量在上的投影向量是( )
A.B.C.D.
5．已知,则( )
A.B.C.D.
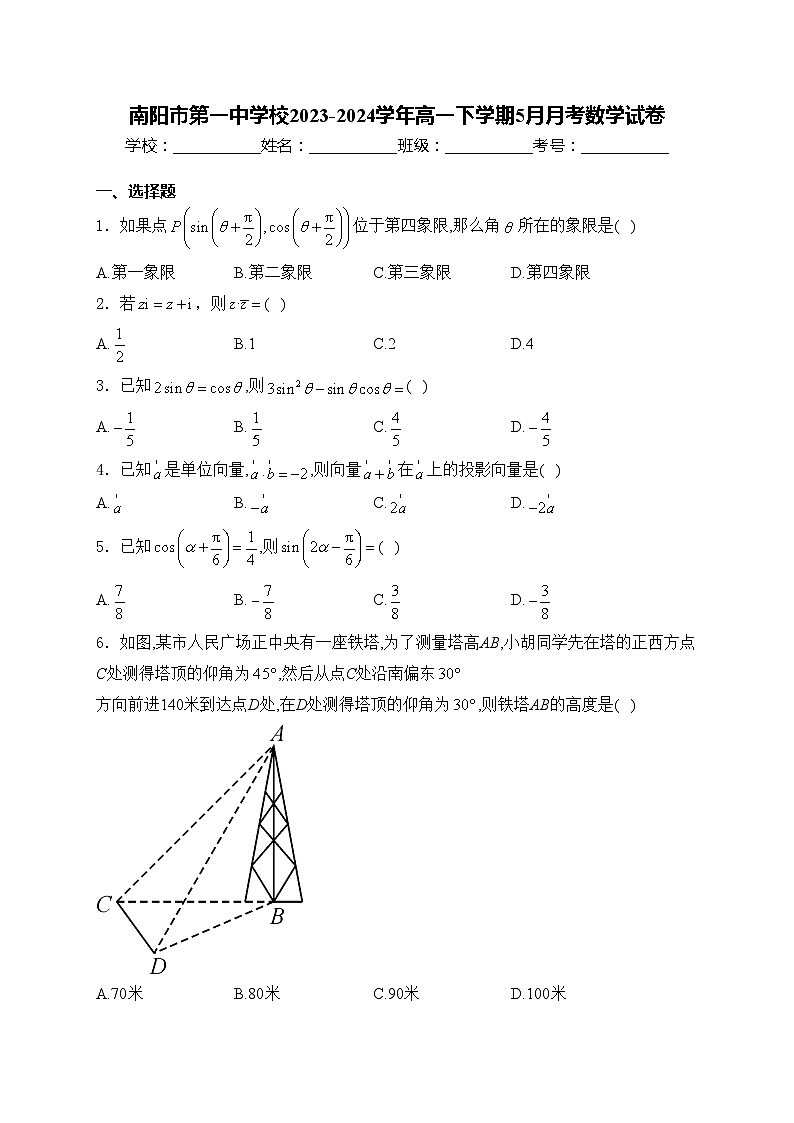
6．如图,某市人民广场正中央有一座铁塔,为了测量塔高AB,小胡同学先在塔的正西方点C处测得塔顶的仰角为,然后从点C处沿南偏东方向前进140米到达点D处,在D处测得塔顶的仰角为,则铁塔AB的高度是( )
A.70米B.80米C.90米D.100米
7．已知函数在上单调递增,且,则( )
A.B.C.D.
8．如图,在正方形ABCD中,,EB和AC相交于点G,且F为AG上一点(不包括端点),若,则的最小值为( )
A.B.C.D.15
二、多项选择题
9．已知复数,则( )
A.
B.复数z的共轭复数为
C.复平面内表示复数z的点位于第一象限
D.复数z是方程的一个根
10．已知函数,则下列说法不正确的是( )
A.若的最小正周期是,则
B.当时,图象对称中心的坐标都可以表示为
C.当时,
D.若在区间上单调递增,则
11．设P为所在平面内一点,则下列说法正确的是( )
A.若,则点P是的重心
B.若,则点P是的垂心
C.若,,则点P是的内心
D.若,则点P是的外心
三、填空题
12．桃湖公园有一扇形花园,扇形的圆心角为,半径为,现要在该花园的周围围一圈护栏,则护栏的总长度为（结果保留）_______________m.
13．若用长度分别为1,2,a的三支木棒拼成一个钝角三角形,则a的取值范围为________.
14．已知函数,将的图象上所有的点向右平移个单位长度得到的图象,若是奇函数,在上恰有1个解,则________.
四、解答题
15．已知,.
（1）求的值;
（2）若,,求的值.
16．在中,角A,B,C所对的边分别为a,b,c,已知.
（1）求角B的大小;
（2）若,,求周长的取值范围.
17．已知向量,,函数.
（1）求函数的解析式和图象的对称中心;
（2）若函数的图象向左平移个单位长度,得到函数的图象,且关于x的方程在上有3个不同的解,求实数的取值范围.
18．函数(,,)的部分图象如图所示.
（1）求函数的解析式;
（2）设函数,若对于任意,,当时,都有成立,求实数t的最大值.
19．奔驰定理是一个关于三角形的几何定理,它的图形形状和奔驰轿车lg相似,因此得名.如图,P是内的任意一点,角A,B,C所对的边分别为a,b,c,总有优美等式:.
（1）若P是的内心,,延长AP交BC于点D,求;
（2）若P是锐角的外心,,,求的取值范围.
参考答案
1．答案：A
解析：由于点P的坐标是,且P在第四象限,故点在第一象限.
故选:A.
2．答案：A
解析：，.
故选：A.
3．答案：B
解析：由得,
所以,
故选:B.
4．答案：B
解析：由题意以及投影向量定义得向量在上的投影向量是:
.
故选:B.
5．答案：A
解析：设,则,,,
.
故选:A
6．答案：A
解析：设塔AB的高度为h,在中,因为,所以;在中,因为,所以;在中,,,,根据余弦定理可得,即,解得或(舍去).故选A.
7．答案：C
解析：当时,,
在上单调递增,,解得:,即,
,,
则由得:,解得:.
故选:C.
8．答案：B
解析：由题可设,,
则由题意得,
因为A,G,C三点共线,故,
所以,
所以,
又A,G,F三点共线,所以,
所以,
当且仅当,即时等号成立,
故最小值为.
故选:B.
9．答案：ACD
解析：
对于A,,故A正确;
对于B,,故B错误;
对于C,复平面内表示复数z点为,在第一象限,故C正确;
对于D,将代入方程中,,等式成立,故D正确.
故选:ACD.
10．答案：BCD
解析：当的最小正周期是时,,则,故A选项正确;
当时,,所以令,,解得,,所以函数的对称中心的坐标为,故B选项不正确;
当时,,,故C选项不正确;
令,,解得,所以函数的单调递增区间为,因为在区间上单调递增,所以,解得,,另一方面,,所以,又因为,所以由,得,由,得,所以的取值范围是,故D选项不正确.
故选:BCD
11．答案：ABD
解析：对于A:若,则.
以,为邻边作平行四边形PADB,M为PD的中点,则,所以,又,所以,
故P为的重心.
所以A正确;
对于B:若,则,
即,即,所以.
同理,则,故P为的垂心.
故B正确;
对于C:在边AB,AC上分别取点E,F,使,,则,以AE,AF为邻边作平行四边形AEGF,则四边形AEGF为菱形.
连接AG,则AG为的角平分线,由,所以点P在角平分线AG上,故点P的轨迹一定通过的内心.
所以C错误;
对于D:若,则,同理有,,故P为的外心.
所以D正确.
故选:ABD
12．答案：
解析：圆心角为,即,
所以扇形的弧长为,周长.
13．答案：
解析：如图,设长度分别为1,2,a的三支木棒分别为的三边AC,AB,BC,
则即,
显然角B为锐角,
当时,由余弦定理得,
或,故;
当时,由余弦定理得,
,故;
综上所述,a的取值范围为.
故答案为:.
14．答案：5
解析：由题意是奇函数,
所以由三角函数奇偶性得,,①,
在上恰有1个解,即在上恰有1个解,
因为时,,
所以在上恰有1个解,
所以由图象性质得,②,
又,所以结合①②得只有当时符合.
故答案为:5.
15．答案：（1）
（2）
解析：（1）由知,故.
所以.
（2）由知,故.
从而,.
所以.
16．答案：（1）或
（2）
解析：（1）由正弦定理和得:
,
故,
又,,所以,即,
又,所以或.
（2）若,则,
所以由（1）,又,
所以由正弦定理得,,
所以
,
又由上,所以,
所以,
所以,即周长的取值范围为.
17．答案：（1）;
（2）
解析：（1）由题,
令,
所以函数图象的对称中心为.
（2）由题得,
因为方程在上有3个不同的解,
所以由二倍角公式得在上有3个不同的解,
因为时,,故是方程的一个解,
所以在上有2个不同的解,
此时,所以即在上有2个不同的解,
图像如下:
所以由三角函数图像可知,即.
故方程在上有3个不同的解,则实数的取值范围为.
18．答案：（1）
（2）
解析：（1）由图象可知,则,
则,
又,所以,
所以,,又,所以,
所以的解析式为;
（2）设函数
令,
则
.
因为对于任意,,当时,都有成立,
所以对于任意,,当时,都有成立,
即对于任意,,当时,都有成立,
所以函数在上单调递减,
由,得,
所以,解得,
所以t的最大值为.
19．答案：（1）
（2）
解析：（1）由于P是的内心,设内切圆的半径为r,
由可得,即,
由,不妨设,
故,
设,则,
故,
由于与共线,而与不共线,
因此必然,故,
（2）设外接圆的半径为R,
则由得,
即,
由于,所以,
因此,又,
所以
,
由于三角形为锐角三角形,所以,解得,
故,
故当时,取最小值,
当或时,,
故.