北师大版九年级上册1 反比例函数习题

这是一份北师大版九年级上册1 反比例函数习题，共33页。试卷主要包含了选择题，四象限，解答题等内容，欢迎下载使用。
1.函数y=−ax+a与y=ax(a≠0)在同一坐标系中的图象可能是( )
A. B. C. D.
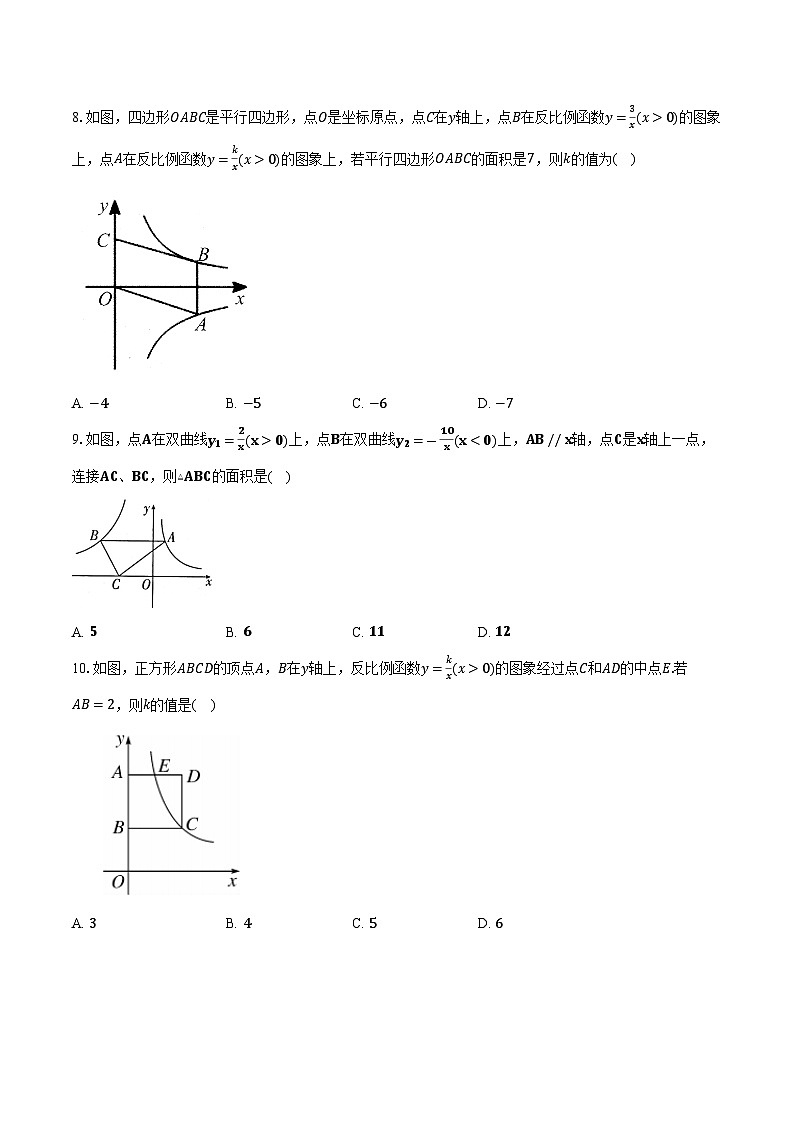
2.如图，点A在反比例函数y1=18x(x>0)的图象上，过点A作AB⊥x轴，垂足为B，交反比例函数y2=6x(x>0)的图象于点C.P为y轴上一点，连接PA，PC.则△APC的面积为( )
A. 5
B. 6
C. 11
D. 12
3.函数y=kx和y=−kx+2(k≠0)在同一平面直角坐标系中的大致图象可能是( )
A. B.
C. D.
4.已知反比例函数y=-3x，下列描述不正确的是( )
A. 图象位于第二、四象限
B. 若点P(x1,y1)，Q(x2,y2)是该函数图象上两点，且x10B. k+b0D. k−b0)的图象上，点A在反比例函数y=kx(x>0)的图象上，若平行四边形OABC的面积是7，则k的值为( )
A. −4B. −5C. −6D. −7
9.如图，点A在双曲线y1=2x(x>0)上，点B在双曲线y2=-10x(x0)的图象经过点C和AD的中点E.若AB=2，则k的值是( )
A. 3B. 4C. 5D. 6
11.如图，已知在平面直角坐标系中，Rt△ABC的顶点A(0,3)，B(3,0)，∠ABC=90°.函数y=4x(x>0)的图象经过点C，则AC的长为( )
A. 3 2B. 2 5C. 2 6D. 26
12.如图所示，四边形OABC是矩形，四边形ADEF是正方形，点A，D在x轴的正半轴上，点C在y轴的正半轴上，点F在AB上，点B、E在反比例函数y=kx(x>0)的图象上，正方形ADEF的面积为9，且BF=53AF，则k值为( )
A. 15B. 714C. 725D. 17
二、填空题：本题共4小题，每小题3分，共12分。
13.如图，点A在双曲线y=6x(x>0)上，过点A作AB⊥x轴于点B，点C在线段AB上且BC：CA=1：2，双曲线y=kx(x>0)经过点C，则k= ．
14.如图，在平面直角坐标系中，O(0,0)，A(3,1)，B(1,2).反比例函数y=kx(k≠0)的图象经过▱OABC的顶点C，则k=______．
15.矩形OABC在坐标系中的位置如图所示，A点坐标为(2 15,0)．C点坐标为(0,5)，反比例函数y=kx的图象交边AB、BC于D、E两点．且∠DOE=45°.则k=______．
16.如图，四边形OABC是菱形，已知A点的坐标是(5,0)，反比例函数y=kx(x>0)经过点C，且OB·AC=40，则这个反比例函数的解析式为 ．
三、解答题：本题共9小题，共72分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题8分)
如图，在平面直角坐标中，点O是坐标原点，一次函数y1=kx+b与反比例函数y2=3x(x>0)的图象交于A(1,m)、B(n,1)两点．
(1)求直线AB的解析式及△OAB面积；
(2)根据图象写出当y10)图象上一点，过点B分别向坐标轴作垂线，垂足为A，C.反比例函数y=kx(x>0)的图象经过OB的中点M，与AB，BC分别相交于点D，E.连接DE并延长交x轴于点F，点G与点O关于点C对称，连接BF，BG．
(1)填空：k=______；
(2)求△BDF的面积；
(3)求证：四边形BDFG为平行四边形．
21.(本小题8分)
如图，一次函数y=12x+1的图象与反比例函数y=kx的图象相交于A(2,m)和B两点．
(1)求反比例函数的解析式；
(2)求点B的坐标．
22.(本小题8分)
已知一次函数y=kx+b的图象直线与反比例函数的y=mx图象双曲线相交于点A(−2,−3)和点B(1,n)，且直线与x轴、y轴相交于点C、点D．
(1)求一次函数和反比例函数的解析式；
(2)点P(p,q)为直线AB上的动点，过P作x轴垂线，交双曲线于点E，交x轴于点F，请选择下面其中一题完成解答(若两题均选择，则只批改第①题)：
①连接DE，若S△PDE=6S△DCO，求PEPF的值；
②点P在点E上方时，判断关于x的方程(p+1)x2+(p−1)x−p−12=0的解的个数．
23.(本小题8分)
如图，在平面直角坐标系xOy中，一次函数y=−x+5的图象与反比例函数y=kx的图象交于点A(1,a)，B两点。
(1)求反比例函数的表达式及点B的坐标;
(2)过点B的直线与x轴正半轴交于点M，与y轴交于点N。若BMMN=13，求△AMN的面积;
(3)点C在第三象限内的反比例函数图象上，横坐标和纵坐标相等。关于原点O的对称点为点D。平面内是否存在点E，使得△ABD∽△ACE?若存在，求E点的坐标;若不存在，请说明理由。
24.(本小题8分)
已知反比例函数y1=k1x(k1≠0)的图象与一次函数y2=k2x+b(k2≠0)的图象交于点A(1,4)和点B(m,−2)．
(1)求这两个函数的关系式；
(2)结合图象直接比较：当x0时，−a0，b0．
根据反比例函数y=2x，k=2>0，x>0，可得其图像位于第一象限，进而得出一次函数y=kx+b的图象经过第一、三、四象限，则k>0，b0)的图象在第四象限，
∴k=−4，
故选：A．
9.【答案】B
【解析】【分析】
本题主要考查的是反比例函数系数k的几何意义，反比例函数的图象上点的坐标特征，三角形的面积的有关知识，连接OA，OB，AB与y轴交于点M，根据AB//x轴得到S△ABC=S△AOB，然后根据S△AOB=S△AOM+S△BOM求解即可
【解答】
解：如图，连接OA，OB，AB与y轴交于点M，

∵AB/​/x轴，点A双在曲线y1=2x(x>0)上，点B在双曲线y2=−10x(x0)的图象经过点C，
∴m(3+m)=4，
解得m=1或−4(负数舍去)，
∴CD=BD=1，
∴BC2=2，
在Rt△ABC中，AB2+BC2=AC2，
∴AC= 18+2=2 5
故选：B．
12.【答案】C
【解析】【分析】
此题主要考查了待定系数法求反比例函数解析式，以及反比例函数图象上点的坐标特点，关键是掌握凡是函数图象经过的点必能满足解析式．设AO的长度为x，根据题意得E点坐标为(x+3,3)，B点坐标为(x,8).再根据B、E在反比例函数y=kx(x>0)的图象上，列出方程3(x+3)=8x，求出x的值，进而可求得k的值．
【解答】
解：设AO的长度为x．
∵正方形ADEF的面积为9，
∴正方形ADEF的边长为3，
∴E(x+3,3)，
∵BF=53AF，
∴BF=53×3=5，
∴B(x,8)．
∵点B、E在反比例函数y=kx(x>0)的图象上，
∴3(x+3)=8x，
解得x=95，
∴k=95×8=725，
故选C．
13.【答案】2
【解析】解：连接OC，
∵点A在双曲线y=6x(x>0)上，过点A作AB⊥x轴于点B，
∴S△OAB=12×6=3，
∵BC：CA=1：2，
∴S△OBC=3×13=1，
∵双曲线y=kx(x>0)经过点C，
∴S△OBC=12|k|=1，
∴|k|=2，
∵双曲线y=kx(x>0)在第一象限，
∴k=2，
故答案为2．
根据反比例函数系数k的几何意义，即可得到结论．
本题考查了反比例函数系数k的几何意义，属于中档题．
14.【答案】−2
【解析】解：如图，连接OB，AC，交于点P，
∵四边形OABC是平行四边形，
∴AP=CP，OP=BP．
∵O(0,0)，B(1,2)，
∴点P的坐标为(12,1)．
∵A(3,1)，
∴点C的坐标为(−2,1)．
∵反比例函数y=kx(k≠0)的图像经过点C，
∴k=−2×1=−2．
本题考查了平行四边形的性质及待定系数法求反比例函数解析式；
连接OB，AC，交于点P，先根据平行四边形的性质求出P点坐标，进一步求出C点坐标，将C点坐标代入y=kx中，即可求出k的值．
15.【答案】15
【解析】【分析】
本题考查的是反比例函数图象上点的坐标特征，矩形的性质，全等三角形的判定与性质有关知识，将OE绕点O顺时针旋转90°得到OM，连接DE、DM，作MN⊥OA于N.由题意可以设E(k5,5)，D(2 15,k2 15)，想办法证明DE=DM，由此构建方程即可解决问题；
【解答】
解：将OE绕点O顺时针旋转90°得到OM，连接DE、DM，作MN⊥OA于N．
∵四边形OABC是矩形，A(2 15,0)，C(0,5)，反比例函数y=kx的图象交边AB、BC于D、E两点，
∴E(k5,5)，D(2 15,k2 15)，
∵∠OCE=∠ONM=90∘，OE=OM，
又∵∠COE+∠EOA=90∘，∠EOA+∠MON=90∘，
∴∠COE=∠MON，
∴△OCE≌△ONM，
∴CE=MN，OC=ON，
∴M(5,−k5)，
∵∠EOD=∠DOM=45∘，OD=OD，OE=OM，
∴△ODE≌△ODM，
∴DE=DM，
∴(k5−2 15)2+(5−k2 15)2=(2 15−5)2+(k2 15+k5)2，
解得k=15或−100(舍弃)．
故答案为：15．
16.【答案】y=12x
【解析】【分析】
本题主要考查的是菱形的性质，勾股定理，待定系数法求反比例函数的解析式，反比例函数的图象上点的坐标特征，反比例函数系数k的几何意义等有关知识．
过点C作CD⊥OA于D，根据A点坐标求出菱形的边长，再根据菱形的面积求得CD，然后利用勾股定理求得OD，从而得到C点坐标，代入函数解析式中求解出k，进而求出此题．
【解答】
解：如图，过点C作CD⊥OA于D，
∵点A的坐标为(5,0)，
∴菱形的边长为OA=5，S菱形OABC=OA⋅CD=12OB⋅AC，
∴5CD=12×40 ，解得CD=4，
在Rt△OCD中，根据勾股定理可得：OD= OC2−CD2=3 ，
∴点C的坐标为(3,4)，
∵双曲线y=kx(k>0)经过点C，
∴k=xy=3×4=12 ，
∴这个反比例函数的解析式为y=12x
17.【答案】解：(1)A(1,m)、B(n,1)两点坐标分别代入反比例函数y2=3x，可得m=3，n=3，
∴A(1,3)、B(3,1)，
把A(1,3)、B(3,1)代入一次函数y1=kx+b，可得
3=k+b1=3k+b，
解得k=−1b=4，
∴直线AB的解析式为y=−x+4．
∴M(0,4)，N(4,0)．
∴S△OAB=S△MON−S△AOM−S△BON=12×4×4−12×4×1−12×4×1=4．
(2)从图象看出0