初中数学人教版八年级上册13.3.1 等腰三角形第1课时教学设计

这是一份初中数学人教版八年级上册13.3.1 等腰三角形第1课时教学设计，共7页。教案主要包含了问题呈现，方法探究，方法总结，方法应用，回顾导入，教学建议，对应训练，随堂训练等内容，欢迎下载使用。

第1课时 等腰三角形的性质
解题大招一 等腰三角形中的分类讨论
类型1 等腰三角形的底角、顶角不明时，需分情况进行讨论，此时注意与三角形内角和定理的结合．
例1 (1)在等腰三角形ABC中，∠A＝130°，求∠B的度数；
(2)在等腰三角形ABC中，∠A＝40°，求∠B的度数．
分析：(1)因为∠A＝130°，根据三角形内角和定理可知，∠A为顶角；
(2)根据三角形内角和定理，因为∠A＝40°<90°，所以分∠B＝∠C或∠A＝∠C或∠A＝∠B三种情况求出∠B的度数．
解：(1)∵∠A＝130°，∴∠A为顶角，∴∠B＝∠C＝eq \f(1,2)(180°－∠A)＝25°.
(2)若∠A为顶角，则∠B＝eq \f(1,2)(180°－∠A)＝70°；
若∠A为底角，∠B为顶角，则∠B＝180°－2×40°＝100°；
若∠A为底角，∠B为底角，则∠B＝40°.
故∠B的度数为70°或100°或40°.
类型2 等腰三角形的腰和底边不明时，需分情况进行讨论，此时需注意各边长应满足三角形的三边关系．
例2 (1)若等腰三角形的周长为26，一边长为8，则腰长为多少？
解：当腰长为8时，三边长为8，8，10.∵8＋8>10，∴能构成三角形．
当底边长为8时，三边长为9，9，8.∵8＋9>9，∴能构成三角形．
故此等腰三角形的腰长为8或9.
(2)若等腰三角形的两边长分别是3和7，则它的周长是多少？
解：分两种情况：
当3为底边长时，其他两边长都为7.三边长3，7，7可以构成三角形，所以周长为17.
当3为腰长时，其他两边长为3和7.因为3＋3＝6<7，所以不能构成三角形，故舍去．
所以等腰三角形的周长为17.
解题大招二 “三线合一”的运用
等腰三角形中的条件转化：
例3 如图，在△ABC中，AB＝AC，AD＝BD，DE⊥AB于点E.若BC＝4，△BDC的周长为10，则AE的长为（ B ）
A．2.5 B．3 C．3.5 D．4
解析：∵BC＝4，且△BDC的周长为10，∴BD＋CD＝10－4＝6.∵AD＝BD，
∴AD＋CD＝6.∴AC＝6.∵AB＝AC，∴AB＝6.∵AD＝BD，DE⊥AB，
∴AE＝eq \f(1,2)AB＝3.故选B.
例4 如图，在△ABC中，AB＝AC，AD是BC边上的中线，E是AB上一点，且DE＝AE.
(1)求证：DE∥AC；
(2)若∠ADE＝24°，求∠C的度数．
分析
(1)证明：∵AB＝AC，AD是BC边上的中线，∴∠CAD＝∠BAD.
∵DE＝AE，∴∠BAD＝∠ADE.∴∠CAD＝∠ADE.∴DE∥AC.
(2)解：∵∠ADE＝24°，∴∠CAD＝∠ADE＝24°.
∵AB＝AC，AD是BC边上的中线，∴AD⊥BC.∴∠ADC＝90°.
∴∠C＝90°－∠CAD＝66°.
例5 下面是证明等腰三角形的性质2——“三线合一”时的三个命题，请完成这三个命题的证明.
分析：命题一：由“SAS”证明△ABD≌△ACD；
命题二：由“SSS”证明△ABD≌△ACD；
命题三：由“HL”证明Rt△ABD≌Rt△ACD.
命题一：证明：∵AD平分∠BAC，∴∠BAD＝∠CAD.
在△ABD和△ACD中，eq \b\lc\{(\a\vs4\al\c1(AB＝AC，,∠BAD＝∠CAD，,AD＝AD，))∴△ABD≌△ACD(SAS)．
∴BD＝CD，∠ADB＝∠ADC＝eq \f(1,2)×180°＝90°.∴AD⊥BC.
命题二：
证明：∵D为BC的中点，∴BD＝CD.
在△ABD和△ACD中，eq \b\lc\{(\a\vs4\al\c1(AB＝AC，,BD＝CD，,AD＝AD，))∴△ABD≌△ACD(SSS)．
∴∠BAD＝∠CAD，∠ADB＝∠ADC＝eq \f(1,2)×180°＝90°.∴AD⊥BC.
命题三：
证明：∵AD⊥BC，∴∠ADB＝∠ADC＝90°.
在Rt△ABD和Rt△ACD中，eq \b\lc\{(\a\vs4\al\c1(AB＝AC，,AD＝AD，))∴Rt△ABD≌Rt△ACD(HL)．∴BD＝CD，∠BAD＝∠CAD.
培优点 构造等腰三角形，利用等腰三角形的性质解题
例 【问题呈现】小强在一次学习过程中遇到了下面的问题：
如图①，在△ABC与△DEF中，AB＝DE，∠1＝∠7，AC＋BC＝DF.求证：∠3＝2∠9.
【方法探究】以下是小强的方法：
证明：如图②，延长AC至点G，使CG＝BC，连接BG.
∵CG＝BC，∴∠4＝∠5.(①)
∴∠3＝∠4＋∠5＝2∠5.
接下来只需证明∠5＝∠9，小强就能解决该问题了．
(1)①中应填写的理论依据为等边对等角．
(2)请补全证明过程．
【方法总结】 从上面的方法可以看出，通过“化折为直”，不仅可以构造等腰三角形，还可以得到角的倍分关系，可谓一举两得．
【方法应用】 (3)如图③，在△ABC与△ADC中，若∠BAC＝∠DAC＝30°，∠ACB＝110°，AD＋CD＝AB，则∠D＝80°.
分析：(1)利用了等腰三角形的性质1——等边对等角；
(2)证明△ABG≌△DEF(SAS)，由全等三角形的性质得出∠5＝∠9，即可得出结论；
(3)延长AD到点E，使DE＝CD，证明△BAC≌△EAC(SAS)，得出∠B＝∠E.由三角形内角和定理得出∠B＝40°，再根据∠ADC＝∠DCE＋∠E可得出答案．
解：(2)补全过程为：∵AC＋BC＝DF，
∴AC＋CG＝DF，即AG＝DF.
在△ABG和△DEF中，eq \b\lc\{(\a\vs4\al\c1(AB＝DE，,∠1＝∠7，,AG＝DF，))∴△ABG≌△DEF(SAS)．∴∠5＝∠9.∴∠3＝2∠9.
(3)解析：如图③，延长AD到点E，使DE＝CD，连接CE，
则AD＋DE＝AD＋CD＝AB，即AE＝AB.
又∠BAC＝∠EAC，AC＝AC，∴△BAC≌△EAC(SAS)．∴∠B＝∠E.
∵∠BAC＝30°，∠ACB＝110°，∴∠B＝180°－∠BAC－∠ACB＝180°－30°－110°＝40°.
∴∠E＝40°.∵DE＝CD，∴∠DCE＝∠E＝40°.∴∠ADC＝∠DCE＋∠E＝40°＋40°＝80°.
教学目标
课题
13.3.1 第1课时 等腰三角形的性质
授课人
素养目标
1.探索并证明等腰三角形的性质：(1)等腰三角形的两个底角相等(“等边对等角”)；(2)等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(“三线合一”).
2.运用等腰三角形的性质进行证明和计算.
3.经历观察、实验、猜想、论证的过程，体会等腰三角形性质的几何证明的逻辑严密性与科学性，提升推理能力.
教学重点
1.探索并证明等腰三角形的性质.
2.运用等腰三角形的性质进行证明和计算.
教学难点
等腰三角形性质的证明.
教学活动
教学步骤
师生活动
活动一：回顾旧知，引入新知
设计意图
回顾等腰三角形、轴对称等相关知识，为后面的探究学习做铺垫.
【回顾导入】
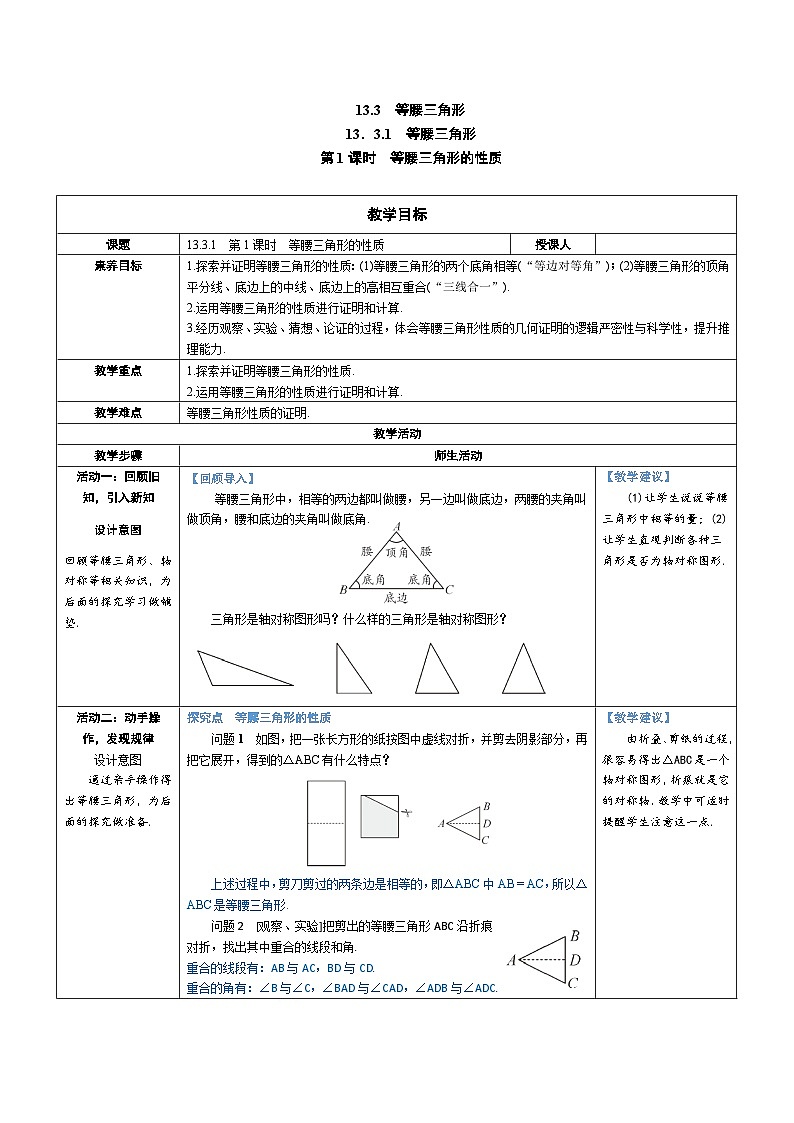
等腰三角形中，相等的两边都叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角.
三角形是轴对称图形吗？什么样的三角形是轴对称图形？
【教学建议】
(1)让学生说说等腰三角形中相等的量；(2)让学生直观判断各种三角形是否为轴对称图形.
活动二：动手操作，发现规律
设计意图
通过亲手操作得出等腰三角形，为后面的探究做准备.
探究点 等腰三角形的性质
问题1 如图，把一张长方形的纸按图中虚线对折，并剪去阴影部分，再把它展开，得到的△ABC有什么特点？
上述过程中，剪刀剪过的两条边是相等的，即△ABC中AB＝AC，所以△ABC是等腰三角形.
问题2 [观察、实验]把剪出的等腰三角形ABC沿折痕
对折，找出其中重合的线段和角.
重合的线段有：AB与AC，BD与CD.
重合的角有：∠B与∠C，∠BAD与∠CAD，∠ADB与∠ADC.
【教学建议】
由折叠、剪纸的过程，很容易得出△ABC是一个轴对称图形，折痕就是它的对称轴．教学中可适时提醒学生注意这一点.
教学步骤
师生活动
设计意图
利用轴对称的性质，引导学生得出等腰三角形的性质，培养综合归纳的能力.
设计意图
让学生经历观察、实验、猜想、论证的过程，体验数学知识的探究方法，感知数学理论的严谨性.
问题3 在等腰三角形ABC中，AD是什么特殊的线段？
既是顶角的平分线，又是底边上的中线，也是底边上的高．
问题4 [猜想]等腰三角形有什么性质？说说你的猜想．
(1)等腰三角形的两个底角相等．
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．
问题5 在一张白纸上任意画一个等腰三角形，把它剪下来，请你试着折一折．你的猜想仍然成立吗？
成立．
归纳：
等腰三角形的性质：
性质1 等腰三角形的两个底角相等(简写成“等边对等角”).
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”).
问题6 [论证]如图，△ABC中，AB＝AC，作底边BC的中线AD.求证：∠B＝∠C，AD平分顶角∠BAC，AD垂直于底边BC.
证明：在△BAD和△CAD中，eq \b\lc\{(\a\vs4\al\c1(AB＝AC，,BD＝CD，,AD＝AD，))
∴ △BAD≌△CAD(SSS)．
∴ ∠B＝∠C.(这样，我们就证明了性质1)
由△BAD≌△CAD，还可以得出∠BAD＝∠CAD，∠BDA＝∠CDA，从而AD⊥BC.这也就证明了等腰三角形ABC底边上的中线AD平分顶角∠BAC并垂直于底边BC.
用类似的方法，还可以证明等腰三角形顶角的平分线平分底边并且垂直于底边，底边上的高平分顶角并且平分底边．这也就证明了性质2.
从以上证明也可以得出，等腰三角形底边上的中线的左右两部分经翻折可以重合，等腰三角形是轴对称图形，底边上的中线(顶角平分线、底边上的高)所在的直线就是它的对称轴．
【对应训练】 教材P77练习第1～3题．
【教学建议】
(1)性质1很容易得出，对于性质2，要引导学生注意对称轴在等腰三角形中的多重含义(顶角平分线、底边上的中线、底边上的高)，从而归纳出“三线合一”．
【教学建议】
性质2实际上包含了三个命题的证明，让学生完成另外两种情况的证明：
(1)把辅助线AD改为底边BC上的高，证明它是顶角的平分线和底边BC上的中线；
(2)把辅助线AD改为顶角∠BAC的平分线，证明它是底边BC上的中线和底边BC上的高．
教学步骤
师生活动
活动三：知识综合，巩固提升
设计意图
通过例1和对应训练1强化学生对等腰三角形性质1的掌握.
通过例2和对应训练2使学生掌握对等腰三角形性质1和性质2的综合运用.
例1 (教材P76例1)如图，在△ABC中，AB＝AC，点D在AC上，且BD＝BC＝AD.求△ABC各角的度数.
解：∵ AB＝AC，BD＝BC＝AD，
∴ ∠ABC＝∠C＝∠BDC，∠A＝∠ABD(等边对等角).
设∠A＝x，则∠BDC＝∠A＋∠ABD＝2x，
从而∠ABC＝∠C＝∠BDC＝2x.
于是在△ABC中，有∠A＋∠ABC＋∠C＝x＋2x＋2x＝180°.
解得x＝36°.
所以，在△ABC中，∠A＝36°，∠ABC＝∠C＝72°.
例2 如图，在△ABC中，AB＝AC，AE是BC边上的中线，BF是角平分线，∠C＝70°.求∠BAE和∠1的度数.
解：∵AB＝AC，∠C＝70°，
∴∠ABC＝∠C＝70°.
∵AB＝AC，AE是BC边上的中线，
∴AE⊥BC，即∠AEB＝90°.
∴∠BAE＝90°－∠ABE＝20°.
∵∠ABC＝70°，BF是∠ABC的平分线，∴∠CBF＝eq \f(1,2)∠ABC＝35°.
由三角形外角的性质可知，
∠1＝∠AEB＋∠CBF＝90°＋35°＝125°.
【对应训练】
1.如图，点D是△ABC中BC边上的一点，且AB＝AC＝CD，AD＝BD，求∠BAC的度数.
解：∵AB＝AC，∴∠B＝∠C.
∵BD＝AD，∴∠B＝∠DAB.
∵AC＝CD，∴∠DAC＝∠ADC＝∠B＋∠BAD＝2∠B.
∴∠BAC＝∠BAD＋∠DAC＝∠B＋2∠B＝3∠B.
又∠B＋∠C＋∠BAC＝180°，∴5∠B＝180°.
∴∠B＝36°.
∴∠BAC＝3∠B＝108°.
2.如图，在△ABC中，AB＝AC，∠BAC＝120°，AD是BC边上的中线，E是AB上一点且BD＝BE，求∠ADE的度数.
解：∵AB＝AC，∠BAC＝120°，∴∠B＝∠C＝eq \f(1,2)(180°－∠BAC)＝30°
∵BD＝BE ∴∠BDE＝∠BED＝eq \f(1,2)(180°－∠B)＝75°
∵AB＝AC，AD是BC边上的中线，
∴∠ADB＝90°.
∴∠ADE＝∠ADB－∠BDE＝90°－75°＝15°.
【教学建议】
通过例1和对应训练1给学生说明，等腰三角形的性质1常与三角形内角和定理结合考查，必要时需用到方程思想.
【教学建议】
通过例2和对应训练2给学生说明，等腰三角形的两个性质要熟练掌握，关于“三线合一”，见到其中一种表述，要迅速将它转化为另外两条线.
教学步骤
师生活动
活动四：随堂训练，课堂总结
【随堂训练】见《创优作业》“随堂小练”册子相应课时随堂训练.
【课堂总结】师生一起回顾本节课所学主要内容，并请学生回答以下问题：
1.等腰三角形的性质1是什么？
2.等腰三角形的性质2是什么？
【知识结构】
【作业布置】
1.教材P81习题13.3第1，3，4，6，7，9，13题.
2.《创优作业》主体本部分相应课时训练．
板书设计
13.3 等腰三角形
13.3.1 等腰三角形
第1课时 等腰三角形的性质
1.“等边对等角”.
2.“三线合一”．
教学反思
本节课通过折叠、裁剪引入等腰三角形，再根据轴对称的特点归纳出等腰三角形的性质，并利用三角形的全等对这些性质进行了证明，培养了学生的推理能力．在如何用几何语言表述要证明的命题时，学生缺乏自主意识，今后要在教学中有意识地对学生多进行这方面的考查.