河南省驻马店市平舆县2023-2024学年八年级下学期期末数学试题

这是一份河南省驻马店市平舆县2023-2024学年八年级下学期期末数学试题，共13页。
1．本试卷共6页，三个大题，满分120分，考试时间100分钟．
2．本试卷上不要答题，请按答题卡上注意事项的要求直接把答案填写在答题卡上，答在试卷上的答案无效．
3．考试结束后，将本试卷和答题卡一并交回．
一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1．如果，那么（ ）．
A．B．C．D．为任意实数
2．下列四个图形中，不能表示函数图象的是（ ）
A．B．
C．D．
3．若一组数据3，x，4，5，6的众数为5，则这组数据的中位数为（ ）
A．6B．5C．4D．3
4．如图1，在中，对角线交于点是对角线上的两点．当满足下列哪个条件时，四边形不一定是平行四边形？（ ）．
A．B．C．D．
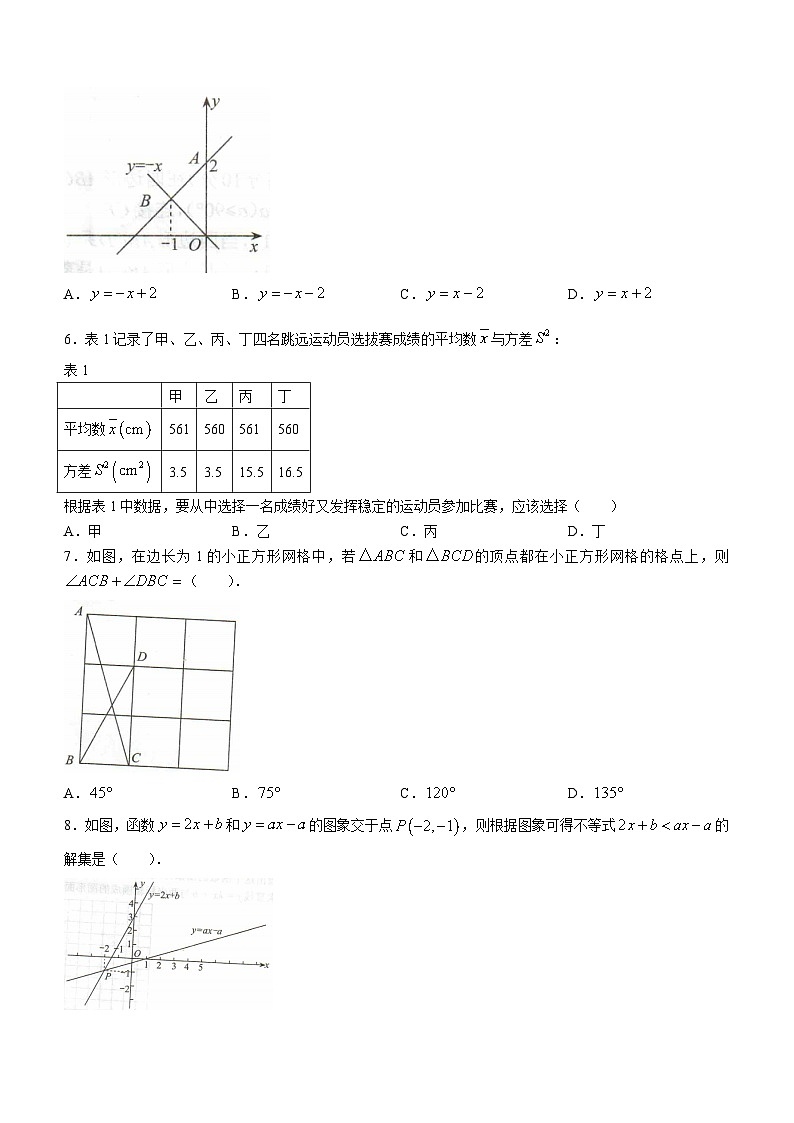
5．如图，一次函数的图象经过点，且与函数的图象交于点，则该一次函数的表达式为（ ）
A．B．C．D．
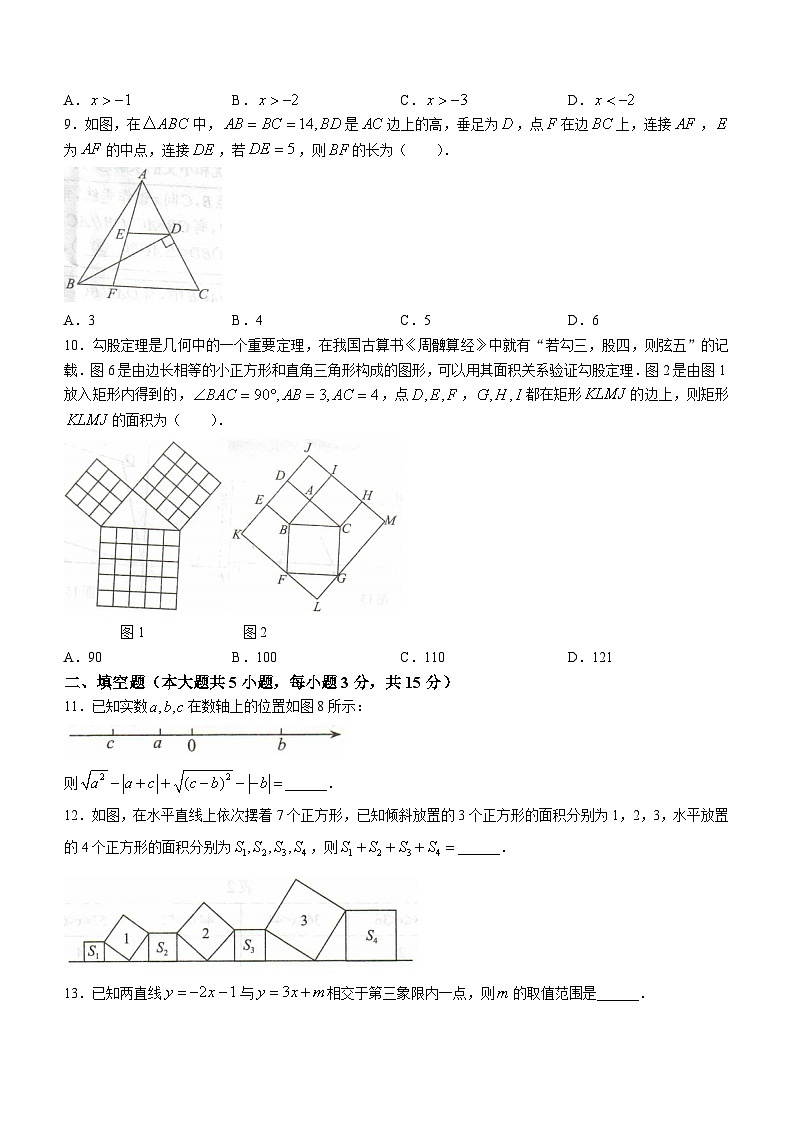
6．表1记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差：
表1
根据表1中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择（ ）
A．甲B．乙C．丙D．丁
7．如图，在边长为1的小正方形网格中，若和的顶点都在小正方形网格的格点上，则（ ）．
A．B．C．D．
8．如图，函数和的图象交于点，则根据图象可得不等式的解集是（ ）．
A．B．C．D．
9．如图，在中，是边上的高，垂足为，点在边上，连接，为的中点，连接，若，则的长为（ ）．
A．3B．4C．5D．6
10．勾股定理是几何中的一个重要定理，在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．图6是由边长相等的小正方形和直角三角形构成的图形，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，，点，都在矩形的边上，则矩形的面积为（ ）．
图1 图2
A．90B．100C．110D．121
二、填空题（本大题共5小题，每小题3分，共15分）
11．已知实数在数轴上的位置如图8所示：
则______．
12．如图，在水平直线上依次摆着7个正方形，已知倾斜放置的3个正方形的面积分别为1，2，3，水平放置的4个正方形的面积分别为，则______．
13．已知两直线与相交于第三象限内一点，则的取值范围是______．
14．已知，若，则______（用含的代数式表示）．
15．如图，在矩形中，是边上一点，连接，把沿折叠，使点落在点处，当为直角三角形时，的长为______．
三、解答题（本大题共8小题，共75分．解答时应写出必要的文字说明、证明过程或演算步骤）
16．（本小题满分10分）
（1）化简：．
（2）解不等式组：
17．（本小题满分9分）有这样一类题目：将化简，如果你能找到两个数，使且，则将变成，然后开方，从而化简．
例如：化简．
解：．
仿照上例化简下列各式：
（1）；（2）．
18．（本小题满分9分）
优优同学参加周末社会实践活动，到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数：
51 36 44 46 40 53 37 47 45 46
32 39 45 55 60 54 60 28 56 41
（1）求后10株西红柿秧上小西红柿个数的平均数、中位数和众数；
（2）若对这20个数按组距为8进行分组，请补全频数分布表2及频数分布直方如图；
表2
（3）通过频数分布直方图分析此大棚中西红柿的长势．
19．（本小题满分9分）
如图，和都是等腰直角三角形，是边上一点．
（1）求证：；
（2）求证：．
20．（本小题满分9分）
已知和是一次函数的两组对应值．
（1）求这个一次函数的表达式；
（2）画出这个函数的图象，并求出它与轴、轴的交点；
（3）求直线与两坐标轴围成的图形面积．
21．（本小题满分9分）
（1）如图1，在平面直角坐标系中，四边形是平行四边形，已知点，如何求顶点的坐标呢？下面是小优和小文的求解思路：
请将①②③处的内容依次填在横线上：______，______，______；
（2）如图3，在平面直角坐标系中，四边形是平行四边形，已知点，求顶点的坐标．
图1 图2 图3
22．（本小题满分10分）问题：探究函数的图象与性质．
优优根据学习函数的经验，对函数的图象与性质进行了探究，下面是优优的探究过程，请补充完整：
（1）在函数中，自变量的取值范围是______．
（2）表3所示的是与的几组对应值．
表3
①______；
②若与为该函数图象上不同的两点，则______．
（3）如图所示，在平面直角坐标系中，描出表3中各组对应值为坐标的点，并根据描出的点画出该函数的大致图象，根据函数图象可知：该函数的最小值为______；该函数图象与轴围成的几何图形的面积是______．
（4）已知直线与函数的图象交于两点，当时，试确定的取值范围．
23．（本小题满分10分）在四边形中，是边上一点，在的右侧作，且，连接．
（1）如图1，当四边形是正方形时，______．
（2）如图2，当四边形是菱形时，求（用含的式子表示）．
（3）在（2）的条件下，且，如图3，连接交于点．若为边的三等分点，请直接写出的长．
图1 图2 图3
2023—2024学年度下学期期末学情测评
八年级数学参考答案
一、选择题
1—5：CCBBD 6—10：ADDBC
二、填空题
11．0 12．4 13． 15．
15．或1 【提示】当为直角三角形时，有两种情况：①当点落在矩形内部时；②当点落在边上时；分别求出的长度，即可得到答案．
【详解】解：当为直角三角形时，有两种情况：
①点落在矩形内部时，如图1所示．连接，
在中，，
．
沿折叠，使点落在点处，
，
当为直角三角形时，只能得到，
点共线，即沿折叠，使点落在对角线上的点处，
有．
设，则．在中，
有，
解得．
②当点落在边上时，如图2所示．此时为正方形，
．
故答案为或1．
三、解答题
16．（本小题满分10分）
（1）．
（2）解不等式①，得；
解不等式②，得．
原不等式组的解集为．
17．（本小题满分10分）
解：．
．
18．（本小题满分9分）
解：（1）后10株西红柿秧上小西红柿个数的数的平均数是；把这些数据从小到大排列：，最中间两个数的平均数是，则中位数是49.5；数据60出现了2次，出现的次数最多，则众数是60．
（2）根据题意填表如下：
补图如下：
（3）此大棚的西红柿长势普遍较好，最少有28个；西红柿个数最集中的株数在第三组，共7株；西红柿的个数分布合理，中间多，两端少．（合理即可给分）
19．（本小题满分9分）
证明：（1）因为和都是等腰直角三角形，所以，所以，即．
所以．
（2）因为和都是等腰直角三角形，，所以．
由（1）知，，所以，所以，所以，即．
20．（本小题满分9分）
解：（1）由题意可得解得
所以这个一次函数的表达式为．
（2）此一次函数与轴的交点为，与轴的交点为，图略．
（3）直线与两坐标轴围成的图形面积．
解：（1）．
（2）方法1：如图，作轴于点，过点作轴的平行线，过点作轴的平行线，两者交于点，则．延长交轴于点．
四边形是平行四边形，
．
．
轴，
．
．
，
．
又点，故点的坐标为．
解法2：在平行四边形中，有．因为原点先水平向右平移4个单位长度，再坚直向上平移1个单位长度，得到点，所以点经过同样的平移方式可得到点，则点的坐标为．
22．（本小题满分10分）
解：（1）函数自变量的取值范围是任意实数．
（2）①把代入，得．
②把代入，得，解得或2024．因为与为该函数图象上不同的两点，所以．
（3）该函数的图象如图所示，由图可得,该函数的最小值为；
该函数图象与x轴围成的几何图形的面积是．
（4）在同一平面直角坐标系中画出函数与函数的图象如图所示，由图象可知，当即时，的取值范围是．
23．（本小题满分10分）
解：（1）．
（2）方法1：如图，在的延长线上取点，使得，则，又，故．
所以，由，得．
所以．
所以．
方法2：如图，连接，因为，所以，，所以，于是，
所以．
（3）或．
【提示】由（2）知，，且．如图，作于点，则．易知，得，则．当时，；当时，．
甲
乙
丙
丁
平均数
561
560
561
560
方差
3.5
3.5
15.5
16.5
个数分组
频数
2
4
小优：如图2，分别过点向轴作垂线，垂足分别为和．
在平行四边形中，有，则①______．
又，故（②______），所以……
小文：在平行四边形中，有，且．因为点水平向右平移3个单位长度得到点，所以点水平向右平移3个单位长度得到点，于是点的坐标为③______．
…
0
1
2
3
4
…
…
2
1
0
0
1
…
个数分组
频数
2
5
7
4
2