2023-2024学年河南省周口市鹿邑县老君台中学七年级（下）期末数学试卷（含答案）

这是一份2023-2024学年河南省周口市鹿邑县老君台中学七年级（下）期末数学试卷（含答案），共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.下列实数中，最小的数是( )
A. 0.01B. −1C. − 3D. 0
2.下列调查中，适宜采用全面调查方式的是( )
A. 调查某品牌签字笔的使用寿命B. 调查某品牌纯电动汽车的抗撞击能力
C. 调查乘坐高铁的乘客是否携带违禁物品D. 了解某品种樱桃的微量元素含量
3.若a>b，则下列不等式不一定成立的是( )
A. 2a>2bB. a−1>b−1C. −a<−bD. |a|>|b|
4.下列说法错误的是( )
A. −3是9的平方根B. 5的平方根是± 5
C. −1的立方根是±1D. 9的算术平方根是3
5.已知关于x的一元一次方程3x−m=+4的解为负数，则m的取值范围是( )
A. m<−4B. m>−4C. m≥4D. m≤−4
6.如图，AB/​/CD，EF与AB，CD分别交于点G，H，∠CHG的平分线HM交AB于点M，若∠EGB=50°，则∠GMH的度数为( )
A. 50°
B. 55°
C. 60°
D. 65°
7.在平面直角坐标系中，线段AB两端点的坐标分别为A(1,0)，B(3,2).将线段AB平移后，A、B的对应点的坐标分别为A1(a,1)，B1(4,b)，则( )
A. a=2，b=1B. a=2，b=3
C. a=−2，b=−3D. a=−2，b=−1
8.无论m为何值，点A(m−3,5−2m)不可能在( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
9.现用190张铁皮做盒子，每张铁皮做8个盒身或做22个盒底，而一个盒身与两个盒底配成一个盒子，设用x张铁皮做盒身，y张铁皮做盒底，则可列方程组为( )
A. x+y=1902×8x=22yB. x+y=1902×22y=8xC. 2y+x=1908x=22yD. 2y+x=1902×8x=22y
10.若关于x的不等式组x−1≤23xx<2(x−a)恰有2个整数解，则a的取值范围是( )
A. 0≤a<12B. 0二、填空题：本题共5小题，每小题3分，共15分。
11.16的平方根是______．
12.已知点P(−1,a)到x轴的距离是3，则a= ______．
13.若关于x，y的二元一次方程组x+2y=k−1, 2x+y=k+1的解互为相反数，则k的值为______．
14.如图，GA//FD，一副三角板如图摆放，∠EDF=60°，∠BAC=45°，若BC/​/DE，下列结论：①EF/​/AB；②∠GAB=30°；③EC平分∠FED；④∠AED=120°.其中正确的是______(填序号)．
15.运行程序如图所示，从“输入实数x”到“结果是否>18”为一次程序操作，若输入x后程序操作进行了两次停止，则x的取值范围是______．
三、解答题：本题共8小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题12分)
(1)计算：| 5−3|+ (−3)2−3−64+ 5；
(2)求x的值：5(x−2)2−125=0；
(3)解方程组：x−y3=44x+3y=16．
17.(本小题10分)
解不等式：
(1)求2x−1≥3x−5的正整数解；
(2)2x−3<53x+1≥−2，并把解集在数轴上表示出来．
18.(本小题8分)
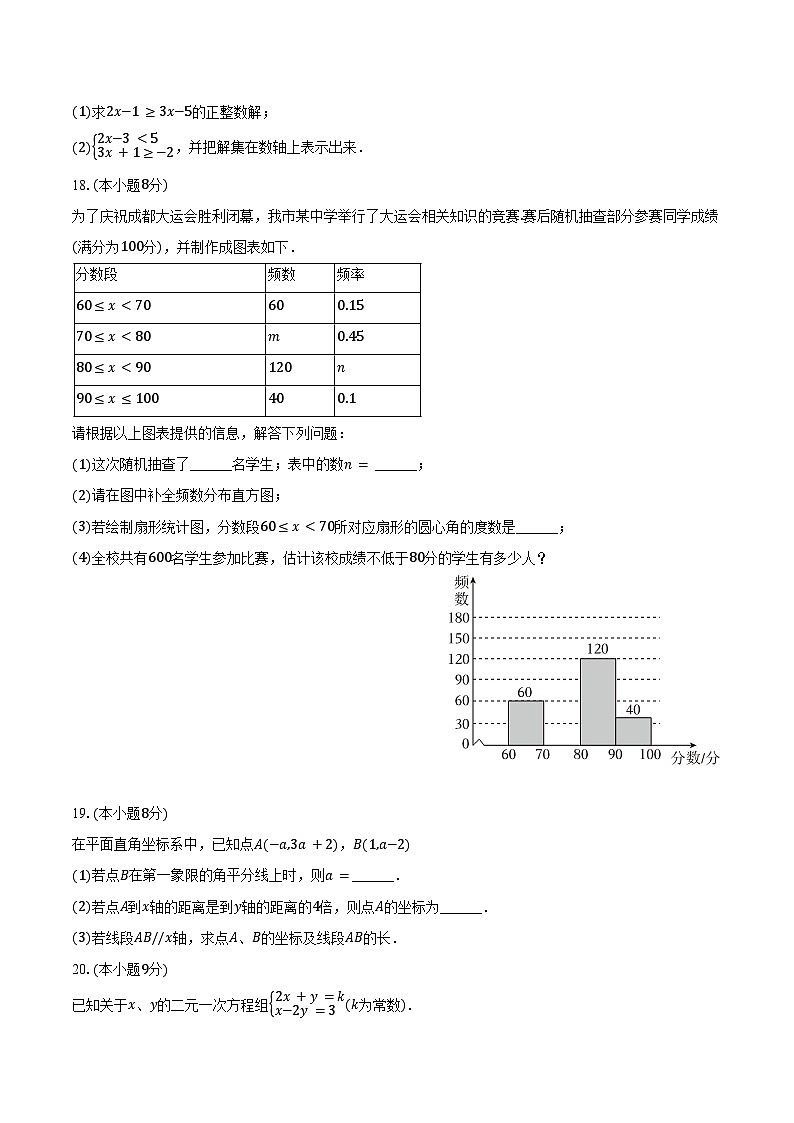
为了庆祝成都大运会胜利闭幕，我市某中学举行了大运会相关知识的竞赛.赛后随机抽查部分参赛同学成绩(满分为100分)，并制作成图表如下．
请根据以上图表提供的信息，解答下列问题：
(1)这次随机抽查了______名学生；表中的数n= ______；
(2)请在图中补全频数分布直方图；
(3)若绘制扇形统计图，分数段60≤x<70所对应扇形的圆心角的度数是______；
(4)全校共有600名学生参加比赛，估计该校成绩不低于80分的学生有多少人？
19.(本小题8分)
在平面直角坐标系中，已知点A(−a,3a+2)，B(1,a−2)
(1)若点B在第一象限的角平分线上时，则a=______．
(2)若点A到x轴的距离是到y轴的距离的4倍，则点A的坐标为______．
(3)若线段AB/​/x轴，求点A、B的坐标及线段AB的长．
20.(本小题9分)
已知关于x、y的二元一次方程组2x+y=kx−2y=3(k为常数)．
(1)若该方程组的解x、y满足3x−y>4，求k的取值范围；
(2)若该方程组的解x、y均为正整数，且k≤12，直接写出该方程组的解．
21.(本小题9分)
根据提示填上每步推理的依据．
如图，已知EF⊥AC于F，DB⊥AC于M，∠1=∠2，∠3=∠C．
求证：AB/​/MN．
证明：∵EF⊥AC，DB⊥AC，
∴∠CFE=∠CMD=90°(______).
∴EF/​/ ______(______).
∴∠2=∠ ______(______).
∵∠1=∠2(已知)，
∴∠1=∠CDM(______).
∴MN//CD(内错角相等，两直线平行)．
∴∠C=∠ ______(______).
∵∠3=∠C(已知)，
∴∠3=∠AMN(等量代换)．
∴AB//MN(______).
22.(本小题9分)
已知：∠1=∠2，EG平分∠AEC．
(1)如图①，∠MAE=45°，∠FEG=15°，∠NCE=75°.试判断EF与CD的位置关系，并说明理由．
(2)如图②，∠MAE=140°，∠FEG=30°，当AB/​/CD时，求∠NCE的度数；
(3)如图②，试写出∠MAE、∠FEG、∠NCE之间满足什么关系时，AB/​/CD．
23.(本小题10分)
如图1，在平面直角坐标系中，点A(−2,0)，B(0,4)，动点C(m,m)在直线L上运动(直线L上所有点的横坐标与纵坐标相等)．

(1)如图2，当点C在第一象限时，依次连接A、B、C三点，AC交y轴于点D，连接OC，
①试求出S△AOC(用含m的式子表示)；
②当S△ABC=5，求出点C的坐标．
(2)如图3，当点C与A、B两点在同一条直线上时，求出C点的坐标；
(3)当10≤S△BOC≤20，求m的取值范围．
参考答案
1.C
2.C
3.D
4.C
5.A
6.D
7.B
8.A
9.A
10.C
11.±4
12.±3
13.0
14.①②③
15.14316.解：(1)| 5−3|+ (−3)2−3−64+ 5
=3− 5+3−(−4)+ 5
=3− 5+3+4+ 5
=10；
(2)5(x−2)2−125=0，
5(x−2)2=125，
(x−2)2=25，
x−2=± 25，
x=2±5，
故x1=7，x2=−3；
(2)x−y3=4①4x+3y=16②，
①×9得：9x−3y=36③，
②+③得：13x=52，
解得：x=4，
把x=4代入②得：16+3y=16，
解得：y=0，
故原方程组的解是：x=4y=0．
17.解：(1)2x−1≥3x−5
移项得，2x−3x≥−5+1
合并同类项得，−x≥−4，
解得：x≤4，正整数解为1，2，3，4
(2)2x−3<5①3x+1≥−2②，
解不等式①得：x<4，
解不等式②得：x≥−1，
∴不等式组的解集为：−1≤x<4．

18.400 0.3 54°
19.解：(1)3；
(2) (−2,8)或(27,87)；
(3)∵线段AB/​/x轴，
∴3a+2=a−2，解得a=−2，
∴A点坐标为(2,−4)，B点坐标为(1,−4).线段AB的长为2−1=1．
20.解：(1)2x+y=k①x−2y=3②，
①+②得，3x−y=k+3，
∵方程组的解x、y满足3x−y>4，
∴k+3>4，
解得k>1；
(2)2x+y=k①x−2y=3②，
①×2+②得5x=2k+3，
①−②×2得5y=k−6，
解得x=2k+35，y=k−65
∵方程组的解x、y均为正整数，且1∴k=11，
∴方程组的解为x=5y=1．
21.垂直定义 DM 同位角相等，两直线平行 CDM 两直线平行，同位角相等 等量代换 AMN 两直线平行，同位角相等 内错角相等，两直线平行
22.解：(1)EF//CD.理由如下：
∵∠1=∠2，∴AB/​/EF，
∴∠AEF=∠MAE，又∠MAE=45°，∠FEG=15°，
∴∠AEG=60°，
∵EG平分∠AEC，∴∠CEG=∠AEG=60°，
∴∠CEF=∠CEG+∠FEG=75°，∠NCE=75°，
∴∠NCE=∠CEF，∴EF/​/CD．
故EF与CD的位置关系是EF//CD．
(2)∵∠1=∠2，∴AB/​/EF，
∴∠FEA+∠MAE=180°，∠MAE=140°，
∴∠FEA=40°，∠FEG=30°，
∴∠AEG=70°，
∵EG平分∠AEC，∴∠CEG=∠AEG=70°，∴∠FEC=100°，
∵AB/​/CD，∴EF/​/CD，
∴∠NCE+∠FEC=180°∴∠NCE=80°．
答：∠NCE的度数为80°．
(3)∠MAE=2∠FEG+∠NCE时，AB/​/CD.理由如下：
由(2)可知：∠AEG=180°−∠MAE+∠FEG，∠FEC=∠FEG+∠NCE，
∠AEG=∠FEC，∠FEC+∠NCE=180°
∴(180°−∠MAE+∠FEG)+(∠FEG+∠NCE)=180°，
整理得：∠MAE=2∠FEG+∠NCE．
故当∠MAE、∠FEG、∠NCE之间满足关系：∠MAE=2∠FEG+∠NCE时，AB/​/CD．
23.解：(1)①A(−2,0)，
∴S△AOC=12×2×m=m，
②当S△ABC=5时，S△ABC=S△AOB+S△OBC−S△AOC，
∴5=12×2×4+12×4m−m，
解得m=1，
∴C(1,1)；
(2)连接OC，如图所示：

则S△AOB=S△BOC−S△AOC，
∴12×2×4=12×4×(−m)−12×2×(−m)，
∴m=−4，
∴C(−4,−4)．
(3)C(m,m)，且10≤S△BOC≤20，
则：①C在第一象限，
S△BOC=12×4×m=2m，
∵10≤S△BOC≤20，
∴10≤2m≤20，
∴5≤m≤10，
②C在第三象限，
S△BOC=12×4×(−m)=−2m，
∵10≤S△BOC≤20，
∴10≤−2m≤20，
∴−10≤m≤−5，
综上所述：5≤m≤10或−10≤m≤−5． 分数段
频数
频率
60≤x<70
60
0.15
70≤x<80
m
0.45
80≤x<90
120
n
90≤x≤100
40
0.1