初中数学北师大版七年级下册2 幂的乘方与积的乘方课前预习ppt课件

这是一份初中数学北师大版七年级下册2 幂的乘方与积的乘方课前预习ppt课件，共22页。PPT课件主要包含了学习目标，复习导入，x10，am+n，amn，底数不变，指数相乘，指数相加，amnamn，am·anam+n等内容，欢迎下载使用。
1.理解并掌握积的乘方的运算法则；（重点）2.掌握积的乘方的推导过程，并能灵活运用.（难点）
1.计算: （1） 10×102× 103 =______ ； （2） (x5 )2=_________.
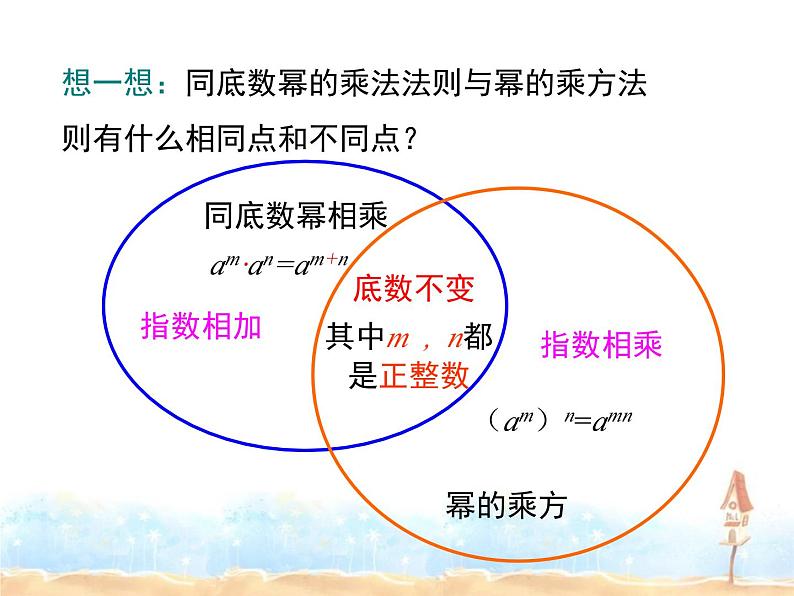
2.（1）同底数幂的乘法：am·an= ( m，n都是 正整数).
（2）幂的乘方：(am)n= (m,n都是正整数）.
其中m , n都是正整数
想一想：同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点？
我们学过的幂的乘方的运算性质适用吗？
我们只能根据乘方的意义及乘法交换律、结合律可以进行运算.
底数为两个因式相乘，积的形式.
（乘法交换律、结合律）
（同底数幂相乘的法则）
思考：积的乘方(ab)n =?
因此可得：(ab)n=anbn (n为正整数).
(ab)n=anbn (n为正整数)
积的乘方法则:积的乘方,等于把积的每一个因式分别乘方，再把所得的幂相乘.
(ab)n = anbn （n为正整数）
想一想：三个或三个以上的积的乘方等于什么？
(abc)n = anbncn （n为正整数）
1.计算（-xy2）3的结果是( )A. x3y6 B. -x3y6 C. -x4y5  D. x4y52.计算：（1）（2y）5； （2）（2xy）2； （3）（x3y）3.
解：原式=32y5.
解：原式=4x2y2.
计算：（1）（2b2）3; （2） ;（3）（2x5y4z3）5; （4）（-3a2）3+（-4a3）2.
1.计算：（1）（3a）2=_____；（2）（-2x3y）2=______；（3） =__________；（4）（-2a2bc3）4=_________.
2.计算：（1）（x2y）4+（x4y2）2；
（2）（2a2）3+（-3a3）2+（a2）2 • a2.
解：原式=x8y4+x8y4 =2x8y4.
解：原式=23·（a2）3+（-3）2·（a3）2+（a2）2·a2=8a6+9a6+a6=18a6.
（1）（-4）2 022×（-0.25）2 021；
解：（1）原式=-4×（-4）2 021×（-0.25）2 021 =-4×［-4×（-0.25）］2 021 =-4×12 021 =-4.
逆用幂的乘方的运算性质
逆用同底数幂的乘法运算性质
逆用积的乘方的运算性质
提示：可利用 简化运算
（2）已知（anbmb）3=a9b15，求2m+n的值.【思路导航】先计算（anbmb）3，再比较相同字母的指数，求出m，n的值，最后计算2m+n的值.
解：因为（anbmb）3=（an）3 •（bm）3 • b3 =a3nb3m+3＝a9b15，所以3n=9，3m+3=15.解得n=3，m=4.所以2m+n=27=128.
（3）已知2n=a，3n=b，24n=c，则a，b，c之间满足怎样的等量关系？【思路导航】将24n化为（23）n • 3n，再得到a，b，c之间满足的等量关系.
解：因为2n=a，3n=b，24n=c，所以c=24n=（8×3）n=（23×3）n=（23）n • 3n=（2n）3 • 3n=a3b.
幂的运算法则的反向应用
an·bn = (ab)n
am+n =am·an
(1)（ab2)3=ab6 ( )
(2) (3xy)3=9x3y3 ( )
(3) (－2a2)2=－4a4 ( )
(4) －(－ab2)2=a2b4 ( )
1.判断:
2.下列运算正确的是（ ） B.(xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4
3. (0.04)2018×[(－5)2018]2=________.
(1) (ab)8; (2) (2m)3; (3) (－xy)5; (4) (5ab2)3; (5) (2×102)2; (6) (－3×103)3.
解：(1)原式=a8·b8;
(2)原式= 23 ·m3=8m3;
(3)原式=(－x)5 ·y5=－x5y5;
(4)原式=53 ·a3 ·(b2)3=125a3b6;
(5)原式=22 ×(102)2=4 ×104;
(6)原式=(－3)3 ×(103)3=－27 ×109=－2.7 ×1010.
（1）2(x3)2·x3－(3x3)3+(5x)2·x7; （2）(3xy2)2+(－4xy3) · (－xy) ; （3）(－2x3)3·(x2)2.
解：原式=2x6·x3－27x9+25x2·x7 = 2x9－27x9+25x9 = 0;
解：原式=9x2y4 +4x2y4 =13x2y4;
解：原式= －8x9·x4 =－8x13.
1.（ab）n=______（n是_______）.积的乘方等于___________________.2.由积的乘方法则，我们可以得到如下结论:（1）（abc）n= _______（n是_______）；（2）anbn=________（n是_______）.