初中数学华师大版八年级上册3 多项式与多项式相乘教学课件ppt

这是一份初中数学华师大版八年级上册3 多项式与多项式相乘教学课件ppt，共23页。PPT课件主要包含了温故知新，-x11，x12y20，x12y12，x7y3z4，+mb，+na，+nb，m+na+b，多项式乘以多项式等内容，欢迎下载使用。

1．理解并掌握多项式与多项式相乘的法则；2．运用多项式与多项式的乘法法则进行运算；
(1)(-x)3·(-x)3·(-x)5=______;(2) (x2)4=_______;(3) (x3y5)4=______; (4)(xy)3·(xy)4·(xy)5=______;(5) (-3x3y)(-5x4y2z4)=___________;(6)-3ab2(-4a+3ab-2)=___________________.
12a2b2-9a2b3+6ab2
某地区在退耕还林期间，将一块长m米、宽a米的长方形林地的长、宽分别增加n米和b米.用两种方法表示这块林地现在的面积，你知道下面的等式蕴含着什么样的运算法则吗？
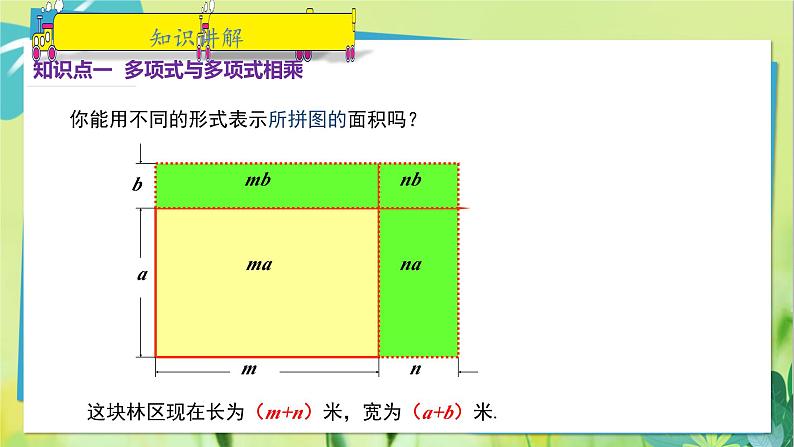
你能用不同的形式表示所拼图的面积吗？
这块林区现在长为（m+n）米，宽为（a+b）米.
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积，故有：
(m+n)(a+b)=
如何进行多项式与多项式相乘的运算 ？
实际上，把(m+n)看成一个整体，有：
= ma+mb+na+nb.
= (m+n)a+(m+n)b
多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加。
多乘多，来计算，多项式各项都见面，乘后结果要相加，化简、排列才算完.
（1）(x+2)(x-3)；
（2）(2x+5y)(3x-2y).
=6x2+11xy-10y2
（1）(m-2n)(m2+mn-3n2)
（2）(3x2-2x+2)(2x+1)
=m· m2 +m·mn-m·3n2-2n·m2-2n·mn+2n·3n2
=m3 +m2n-3mn2-2m2n-2mn2+6n3
=m3-m2n-5mn2+6n3
=6x3+3x2-4x2-2x+4x+2
=6x3-x2+2x+2
（1）(x+5)(x-7)；
（2）(x+5y)(x-7y)；
（3）(2m+3n)(2m-3n)；
（4）(2a+3b)2.
=x2-7x+5x-35
=x2-7xy+5xy-35y2
=x2-2xy-35y2
=4m2+6mn-6mn-9n2
=4a2+12ab+9b2
1．若(x-1)(x+m)=x2+2x+n，则常数n的值为（    ）A．3 B．2C．-3 D．-2
【详解】解：∵(x-1)(x+m)=x2+(m-1)x-m，∴m-1=2,n=-m，解得：m=3,n=-3.故选：C
2．若(-2x-a)(x+5)的积中不含x的一次项，则a的值为（    ）A．10 B．-10 C．5 D．-5
【详解】(-2x-a)(x+5)=-2x2-10x-ax-5a=-2x2-(10+a)x-5a由题意得，10+a=0，解得：a=-10，故选择：B
3．有若干张如图所示的正方形A，B和长方形C卡片，如果要拼一个长为(2a+b)，宽为(a+2b)的长方形，则需要C卡片的张数为(    )  A．5B．4C．3D．2
【详解】解：∵(2a+b)(a+2b)=2a2+5ab+2b2，∴需要C卡片的张数为5张，故选：A．
4．已知x满足(x-2020)(x-2024)=516，则(x-2022)2的值是（    ）A．512B．516C．520D．1032
【详解】解：∵(x-2020)(x-2024)=516，∴(x-2022)2=(x-2020-2)(x-2024+2)=(x-2020)(x-2024)+2(x-2020)-2(x-2024)-4=516+2[(x-2020)-(x-2024)]-4=516+2×4-4=520.故选C．
5．若x+y=3，xy=-2，则(1+x)(1+y)的值是 ．
【详解】解：∵x+y=3，xy=-2，∴(1+x)(1+y)=1+x+y+xy=1+(x+y)+xy=1+3+(-2)=2，故答案为：2．
6．我国古代的许多创新和发展都位居世界前列，如南宋数学家杨辉所著的《详解九章算法》中用如图的三角形解释(a+b)n的展开式的各项系数，此三角形称为“杨辉三角”．根据“杨辉三角”计算(a+b)20的展开式中第三项的系数为 ．  
7．计算(x+y)(x-3y)-3y(nx-y)（n为常数）的值，把x，y的值代入计算时，粗心的小明把y的值看错了，其结果等于9，细心的小红把正确的x，y的值代入计算，结果恰好也是9，为了探个究竟，小红又把y的值随机地换成了2023，结果竟然还是9，根据以上情况，探究其中的奥妙，可以推断出n的值为 ．
8．计算：(1)(x-2y)(x+y)； (2)(m-n)(n-m)．
【详解】（1）解：原式=x2+xy-2xy-2y2=x2-xy-2y2；（2）解：原式=mn-m2-n2+mn=-n2-m2+2mn．
10．小亮想把一个长为50cm，宽为35cm的长方形硬纸片做成一个无盖的长方体盒子，于是在长方形的四个角各剪去一个相同小正方形（如图），设小正方形的边长为xcm．  (1)求图中阴影部分的面积为S（用含x的代数式表示，要求化简）．(2)当x=10cm时，求这个盒子的体积．
【详解】（1）解：依题意，S=(50-2x)(35-2x)=-4x2-170x+1750；（2）当x=10时，3×15×10=4500cm3．答：当x=10cm时，盒子的体积为4500cm3．