华师大版八年级上册第13章 全等三角形13.2 三角形全等的判定4 角边角课堂教学ppt课件

这是一份华师大版八年级上册第13章 全等三角形13.2 三角形全等的判定4 角边角课堂教学ppt课件，共29页。PPT课件主要包含了温故知新，SAS，角边角，角角边，三角形能唯一确定，实验手册附录D，小组交流验证，“角边角”判定方法，几何语言，典例精析等内容，欢迎下载使用。

1、通过画图、操作、实验等教学活动，探索三角形全等的判定方法（，）；2、会用，判定两个三角形全等；3、灵活地运用所学的判定方法判定两个三角形全等，从而解决线段或角相等的问题；
上节课，我们得到了全等三角形的一种判定方法，还记得吗？
现在我们讨论两角一边的情况：如果两个三角形有两个角、一条边分别对应相等，那么这两个三角形全等吗？
可以分成两种情况：（1）两个角及这两角的夹边；（2）两个角及其中一角的对边.
问题：如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带哪一块去呢？你能帮这位同学出主意吗？
操作1：如图，用纸板挡住了两个三角形的一部分，你能画出这两个三角形吗？如果能，你画的三角形与其他同学画的三角形能完全重合吗？
相当于已知一角画三角形，我们可以画出无数个不同形状、大小的三角形.
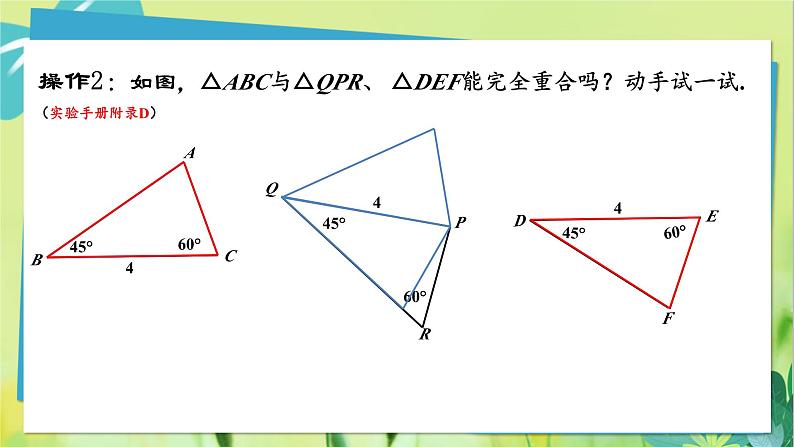
操作2：如图，△ABC与△QPR、 △DEF能完全重合吗？动手试一试.
操作3：按下列作法，用直尺和圆规作△ABC，使AB＝a, ∠A＝∠α, ∠B＝∠β，
1你作的三角形与其他同学作的三角形能完全重合吗？你有什么发现？
作法：1．作AB＝a．2．在AB的同一侧分别作∠MAB＝∠α ，∠NBA＝∠β ，AM、BN相交于点C．3．分别连接AB、AC．△ABC就是所求作的三角形．
文字语言：两角及其夹边分别相等的两个三角形全等(简写成“角边角”或“”）.
例1、如图，已知∠ABC=∠DCB，∠ACB = ∠DBC．求证: △ABC ≌△DCB，AB = DC.
解：在△ABC 和△DCB 中，∵∠ABC =∠DCB （已知），BC = CB（公共边），∠ACB = ∠DBC（已知），∴△ABC≌△DCB（ ）.∴AB = DC（全等三角形的对应边相等）.
例2 已知：如图，在△ABC中，D是BC的中点，点E、F分别在AB、AC上，且DE//AC，DF//AB．求证：BE＝DF，DE＝CF．
1.如图，∠C＝∠E，∠1＝∠2，BA＝DA，你能证明BC＝DE吗?
2.已知：点D在AB上，点E在AC上，BE和CD相交于点O，AB=AC，∠B=∠C
(1)求证：△ABE≌△ACD
∴△ACD≌△ABE（ASA）
(2) ∵△ACD≌△ABE（已证） ∴AD=AE（全等三角形的对应边相等） 又∵AB=AC（已知） ∴AB-AD=AC-AE（等式性质） ∴BD=CE
(2) BD和CE相等吗?
如图，如果两个三角形有两个角分别对应相等，且其中一组相等的角的对边相等，那么这两个三角形是否一定全等？
分析：因为三角形的内角和等于180°，因此有两个角对应相等，那么第三个角必定对应相等，于是有“角边角”，可证得这两个三角形全等.
已知：如图，∠A＝∠A′,∠B＝∠B′,AC＝A′C′.
求证：　△ABC≌△A′B′C′.
证明：∵∠A＝∠A′，∠B＝∠B′， ∠A＋∠B＋∠C＝180°，∠A′＋∠B′＋∠C′＝180°(三角形内角和等于180°)， ∴∠C＝∠C′（等量代换）． 在△ABC和△A′B′C′中， ∵∠A＝∠A′， AC＝A′C′， ∠C＝∠C′， ∴△ABC≌△A′B′C′（）
文字语言：有两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“”）.
例3 如图，点D在AB上，点E在AC上，AD=AE, ∠B=∠C,求证：AB=AC.
分析：证明△ACD≌△ABE,就可以得出AB=AC.
方法归纳：通常利用全等三角形的对应边相等来证明两条线段相等，这是一个重要的方法.类似的方法可以证明两个角相等.
例4.已知：如图， AB⊥BC，AD⊥DC，∠1=∠2, 求证：AB=AD.
证明： ∵ AB⊥BC，AD⊥DC，
∴ ∠ B=∠D=90 °.
在△ABC和△ADC中，
∴ △ABC≌△ADC（).
1、如图，在△ABC中，D 是边 BC 的中点，过点C 画直线 CE，使 CE// AB，交 AD 的延长线于点 E．求证: AD = ED.
证明: CE // AB (已知)，∵∠ABD = ∠ECD，∠BAD = ∠CED (两直线平行，内错角相等).在△ABD 与 △ECD 中，∵∠ABD = ∠ECD，∠BAD = ∠CED (已证)，BD = CD (已知)，∴△ABD≌△ECD ( ) ，∴AD = ED (全等三角形的对应边相等).
2.如图∠ACB=∠DFE，BC=EF，那么应补充一个条件 ，才能使△ABC≌△DEF （写出一个即可）.
3.如图，已知点?在△???的外部，点?在??边上，??交??于?，若 ∠?=∠?=∠?，??=??，则有( )
提示：由∠2=∠3可得∠C=∠E
4.如图，E、F 在线段AC上，DF∥BE，AE=CF．若∠A =∠C， 求证：DF=BE．
5.点B、F、C、E在直线l上(点F、C之间不能直接测量)，点A、D在l的异侧，AB∥DE、∠A=∠D，测得AB=DE.(1)求证:△ABC≌△DEF;(2)若BE=12 m，BF=4 m,求FC的长度.
6.已知：如图，在△ABC中，BE⊥AE，CF⊥AE，BE、CF与AE分别交于点E、F.
（2）如果BE=CF，那么AD是△ABC的中线吗？为什么？
7. 如图，∠DCE=90°，CD=CE，DA⊥AC，EB⊥AC，垂足分别为A、B.(1)求证:△ACD≌ △BEC；
解：(2)线段AD、AB、BE之间的数量关系是:AD+AB=BE.证明如下:∵△ACD≌ △BEC,∴AD=BC,AC=BE.∴AD+AB=BC+AB=AC.∴AD+AB=BE.