高考数学一轮复习考点探究与题型突破第46讲直线的倾斜角与斜率、直线方程(原卷版+解析)

这是一份高考数学一轮复习考点探究与题型突破第46讲直线的倾斜角与斜率、直线方程(原卷版+解析)，共12页。试卷主要包含了直线的方向向量，直线的倾斜角，直线的斜率，直线方程的五种形式等内容，欢迎下载使用。

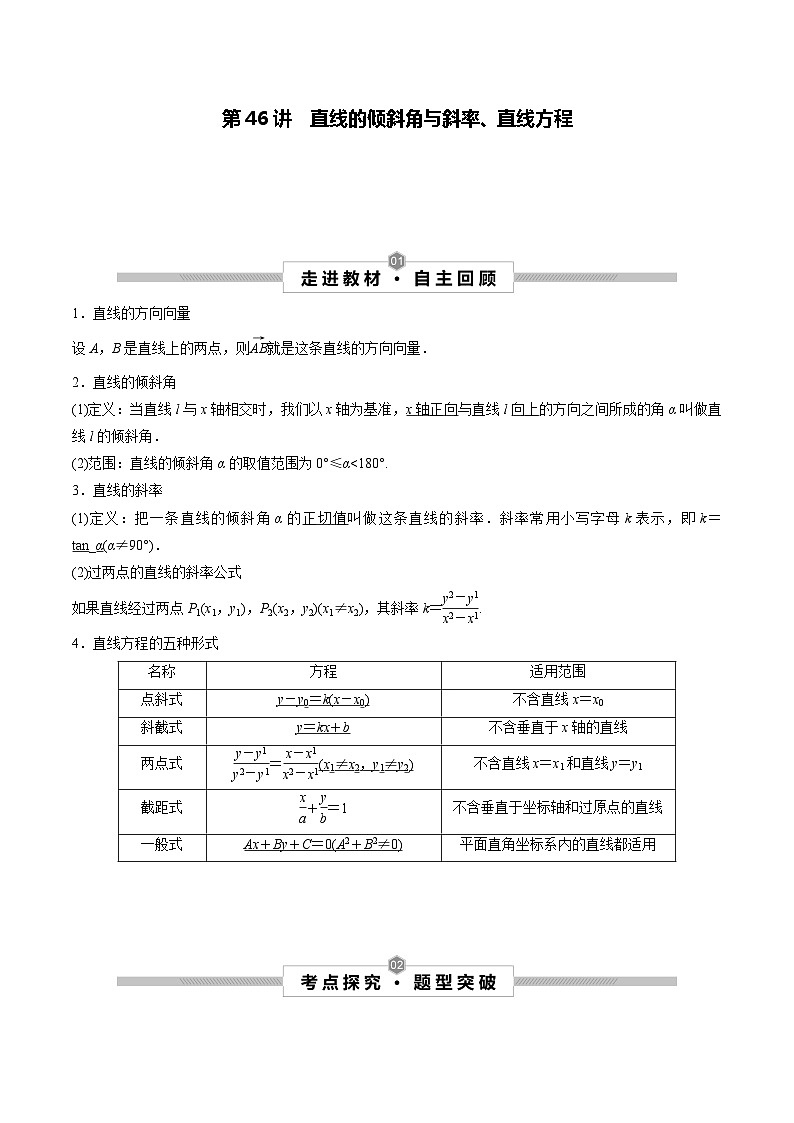
1．直线的方向向量
设A，B是直线上的两点，则eq \(AB,\s\up6(→))就是这条直线的方向向量．
2．直线的倾斜角
(1)定义：当直线l与x轴相交时，我们以x轴为基准，x轴正向与直线l向上的方向之间所成的角α叫做直线l的倾斜角．
(2)范围：直线的倾斜角α的取值范围为0°≤α0.
∵S＝eq \f(1,2)·|OA|·|OB|＝eq \f(1,2)·eq \b\lc\|\rc\|(\a\vs4\al\c1(\f(1＋2k,k)))·|1＋2k|＝eq \f(1,2)·eq \f(（1＋2k）2,k)＝eq \f(1,2)eq \b\lc\(\rc\)(\a\vs4\al\c1(4k＋\f(1,k)＋4))
≥eq \f(1,2)×(2×2＋4)＝4，
当且仅当4k＝eq \f(1,k)，即k＝eq \f(1,2)，等号成立，
∴Smin＝4，此时直线l的方程为x－2y＋4＝0.
[举一反三]
已知直线l过点M(2，1)，且分别与x轴的正半轴，y轴的正半轴交于A，B两点，O为原点，当△AOB面积最小时，求直线l的方程.
解 法一 设直线l的方程为
y－1＝k(x－2)，
则可得Aeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2k－1,k)，0))，B(0，1－2k).
∵l与x轴，y轴正半轴分别交于A，B两点，
∴eq \b\lc\{(\a\vs4\al\c1(\f(2k－1,k)＞0，,1－2k＞0，))∴k＜0.
于是S△AOB＝eq \f(1,2)·|OA|·|OB|
＝eq \f(1,2)·eq \f(2k－1,k)·(1－2k)＝eq \f(1,2)eq \b\lc\(\rc\)(\a\vs4\al\c1(4－\f(1,k)－4k))
≥eq \f(1,2)eq \b\lc\[\rc\](\a\vs4\al\c1(4＋2\r(\b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,k)))·（－4k）)))＝4.
当且仅当－eq \f(1,k)＝－4k，即k＝－eq \f(1,2)时，△AOB面积有最小值为4，此时，直线l的方程为y－1＝－eq \f(1,2)(x－2)，
即x＋2y－4＝0.
法二 设所求直线l的方程为eq \f(x,a)＋eq \f(y,b)＝1(a＞0，b＞0)，则eq \f(2,a)＋eq \f(1,b)＝1.
又∵eq \f(2,a)＋eq \f(1,b)≥2eq \r(\f(2,ab))，∴eq \f(1,2)ab≥4，当且仅当eq \f(2,a)＝eq \f(1,b)＝eq \f(1,2)，
即a＝4，b＝2时，△AOB面积S＝eq \f(1,2)ab有最小值为4.
此时，直线l的方程是eq \f(x,4)＋eq \f(y,2)＝1，即x＋2y－4＝0.
名称
方程
适用范围
点斜式
y－y0＝k(x－x0)
不含直线x＝x0
斜截式
y＝kx＋b
不含垂直于x轴的直线
两点式
eq \f(y－y1,y2－y1)＝eq \f(x－x1,x2－x1)(x1≠x2，y1≠y2)
不含直线x＝x1和直线y＝y1
截距式
eq \f(x,a)＋eq \f(y,b)＝1
不含垂直于坐标轴和过原点的直线
一般式
Ax＋By＋C＝0(A2＋B2≠0)
平面直角坐标系内的直线都适用