高考数学一轮复习知识点讲解+真题测试专题5.5函数y＝Asin(ωx＋φ)的图象及其应用(真题测试)(原卷版+解析)

这是一份高考数学一轮复习知识点讲解+真题测试专题5.5函数y＝Asin(ωx＋φ)的图象及其应用(真题测试)(原卷版+解析)，共27页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

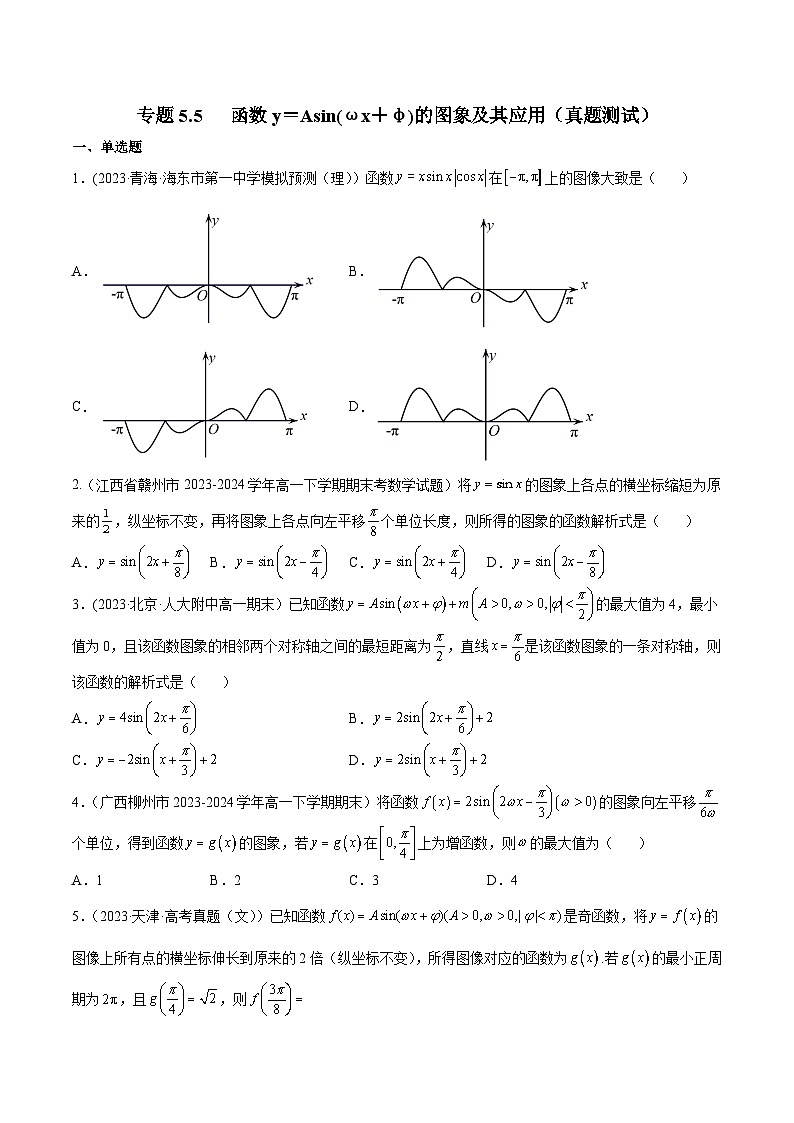
1．(2023·青海·海东市第一中学模拟预测（理））函数在上的图像大致是（ ）
A．B．
C．D．
2.（江西省赣州市2023-2024学年高一下学期期末考数学试题）将的图象上各点的横坐标缩短为原来的，纵坐标不变，再将图象上各点向左平移个单位长度，则所得的图象的函数解析式是（ ）
A．B．C．D．
3．(2023·北京·人大附中高一期末）已知函数的最大值为4，最小值为0，且该函数图象的相邻两个对称轴之间的最短距离为，直线是该函数图象的一条对称轴，则该函数的解析式是（ ）
A．B．
C．D．
4．（广西柳州市2023-2024学年高一下学期期末）将函数的图象向左平移个单位，得到函数的图象，若在上为增函数，则的最大值为（ ）
A．1B．2C．3D．4
5．（2023·天津·高考真题（文））已知函数是奇函数，将的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图像对应的函数为.若的最小正周期为，且，则
A．B．C．D．
6．(2023·全国·高考真题（理））已知曲线C1：y=cs x，C2：y=sin (2x+)，则下面结论正确的是
A．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2
B．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2
C．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2
D．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2
7．(2023·天津·高考真题（文））将函数的图象向右平移个单位长度，所得图象对应的函数
A．在区间 上单调递增B．在区间 上单调递减
C．在区间 上单调递增D．在区间 上单调递减
8．（2023·全国·高考真题（理））关于函数有下述四个结论：
①f(x)是偶函数 ②f(x)在区间（,）单调递增
③f(x)在有4个零点 ④f(x)的最大值为2
其中所有正确结论的编号是
A．①②④B．②④C．①④D．①③
二、多选题
9．(2023·河北承德·高一阶段练习）将函数图像上所有点的纵坐标伸长为原来的3倍，横坐标缩短为原来的，再将所得的图像向右平移个单位长度，得到函数的图像，则（ ）
A．B．的图像关于直线对称
C．的图像关于点对称D．在上单调递增
10.(2023·全国·模拟预测）将函数的图象向右平移个单位，得到的图象关于y轴对称，则下列说法正确的是（ ）
A．最小正周期的最大值为
B．最小正周期的最大值为
C．当的最小正周期取最大值时，平移后的函数在上单调递增
D．当的最小正周期取最大值时，平移后的函数在上单调递减
11．(2023·贵州·六盘水市第二中学高一阶段练习）已知函数的部分图像如图所示，则下列说法正确的是（ ）
A．的图像关于点对称B．的图像关于直线对称
C．在上为增函数D．把的图像向右平移个单位长度，得到一个奇函数的图像
12．(2023·全国·南京外国语学校模拟预测）若函数，则下列说法正确的是（ ）
A．函数的图象可由函数的图象向右平移个单位长度得到
B．函数的图象关于直线对称
C．函数的图象关于点对称
D．函数在上为增函数
三、填空题
13．（2023·江苏·高考真题）将函数y=的图象向右平移个单位长度，则平移后的图象中与y轴最近的对称轴的方程是____.
14．（2023·长岭县第二中学高三三模）函数的图象关于点_______成中心对称，记函数的最大值为，最小值为，则_______．
15．(2023·重庆·高考真题（文））将函数图像上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移个单位长度得到的图像，则______.
16．（2023·山东高三月考）已知定义在上函数（）振幅为2，满足，且．则上零点个数最少为______．
四、解答题
17．(2023·上海市嘉定区第二中学高一期末）已知函数的部分图像如图所示.
(1)求的解析式及对称中心；
(2)先将的图像纵坐标缩短到原来的倍，再向右平移个单位后得到的图像，求函数在上的单调减区间和最值.
18.（2023·天津·静海一中高三月考）已知函数为奇函数，且图象的相邻两对称轴间的距离为.
（1）求的解析式.
（2）求的最大值.
（3）将函数的图象向右平移个单位长度，再把横坐标缩小为原来的(纵坐标变)，得到函数的图象，求的解析式.
19．(2023·上海市新场中学高一期末）已知函数，
(1)求函数的最小正周期；
(2)若求的值域；
(3)将函数图象向右平移个单位后，得到函数的图象，求函数的零点.
20．(2023·北京·北师大实验中学高一期中）某游乐场的摩天轮示意图如图．已知该摩天轮的半径为30米，轮上最低点与地面的距离为2米，沿逆时针方向匀速旋转，旋转一周所需时间为分钟．在圆周上均匀分布12个座舱，标号分别为1～12（可视为点），现从图示位置，即1号座舱位于圆周最右端时开始计时，旋转时间为t分钟．
(1)当时，求1号座舱与地面的距离；
(2)在前24分钟内，求1号座舱与地面的距离为17米时t的值；
(3)记1号座舱与5号座舱高度之差的绝对值为H米，若在这段时间内，H恰有三次取得最大值，求的取值范围．
21.(2023·福建·高考真题（文））已知函数．
（1）求函数的最小正周期；
（2）将函数的图象向右平移个单位长度，再向下平移（）个单位长度后得到函数的图象，且函数的最大值为2．
（ⅰ）求函数的解析式； （ⅱ）证明：存在无穷多个互不相同的正整数，使得．
22．(2023·上海市嘉定区第一中学高一期末）某小区拟用一块半圆形地块（如图所示）建造一个居民活动区和绿化区．已知半圆形地块的直径千米，点O是半圆的圆心，在圆弧上取点C、D，使得，把四边形ABCD建为居民活动区，并且在居民活动区周围铺上一条由线段AB，BC，CD和DA组成的塑胶跑道，其它部分建为绿化区．设，且；
(1)当时，求四边形ABCD的面积；
(2)求塑胶跑道的总长l关于的函数关系式；
(3)当为何值时，塑胶跑道的总长l最短，并求出l的最小值．（答案保留2位小数）
专题5.5 函数y＝Asin(ωx＋φ)的图象及其应用（真题测试）
一、单选题
1．(2023·青海·海东市第一中学模拟预测（理））函数在上的图像大致是（ ）
A．B．
C．D．
答案：D
【解析】
分析：
利用函数的单调性，奇偶性和特值点等性质来判断图像.
【详解】
易知f(x)是偶函数，排除B，C项；
当时，，所以，排除A项.
故选：D
2.（江西省赣州市2023-2024学年高一下学期期末考数学试题）将的图象上各点的横坐标缩短为原来的，纵坐标不变，再将图象上各点向左平移个单位长度，则所得的图象的函数解析式是（ ）
A．B．C．D．
答案：C
【解析】
分析：
直接利用三角函数的图象的平移变换和伸缩变换的应用求出结果.
【详解】
将的图象上各点的横坐标缩短为原来的，纵坐标不变，可得；
再将图象上各点向左平移个单位长度，可得.
故选：C
3．(2023·北京·人大附中高一期末）已知函数的最大值为4，最小值为0，且该函数图象的相邻两个对称轴之间的最短距离为，直线是该函数图象的一条对称轴，则该函数的解析式是（ ）
A．B．
C．D．
答案：B
【解析】
分析：
由题意可得，求出，再由该函数图象的相邻两个对称轴之间的最短距离为，可求出，由直线是该函数图象的一条对称轴，可得，从而线结合已知条件可求出，进而可求得函数的解析式
【详解】
因为函数的最大值为4，最小值为0，
所以，解得，
因为该函数图象的相邻两个对称轴之间的最短距离为，
所以，所以，
所以，得，
所以，
因为直线是该函数图象的一条对称轴，
所以，得，
因为，所以，
所以，
故选：B
4．（广西柳州市2023-2024学年高一下学期期末）将函数的图象向左平移个单位，得到函数的图象，若在上为增函数，则的最大值为（ ）
A．1B．2C．3D．4
答案：A
【解析】
分析：
函数的图象向左平移个单位，得到函数的表达式，然后利用在上为增函数，说明，利用周期公式，求出，得到的最大值.
【详解】
函数的图象向左平移个单位，
得到函数，
在上为增函数，所以，即，即，
所以的最大值为1.
故选：A.
5．（2023·天津·高考真题（文））已知函数是奇函数，将的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图像对应的函数为.若的最小正周期为，且，则
A．B．C．D．
答案：C
【解析】
只需根据函数性质逐步得出值即可．
【详解】
因为为奇函数，∴；
又
，，又
∴，
故选C．
6．(2023·全国·高考真题（理））已知曲线C1：y=cs x，C2：y=sin (2x+)，则下面结论正确的是
A．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2
B．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2
C．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2
D．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2
答案：D
【解析】
【详解】
把C1上各点的横坐标缩短到原来的倍，纵坐标不变，得到函数y=cs2x图象，再把得到的曲线向左平移个单位长度，得到函数y=cs2（x+）=cs（2x+）=sin（2x+）的图象，即曲线C2，
故选D．
点睛：三角函数的图象变换，提倡“先平移，后伸缩”，但“先伸缩，后平移”也常出现在题目中，所以也必须熟练掌握.无论是哪种变形，切记每一个变换总是对字母而言. 函数是奇函数；函数是偶函数；函数是奇函数；函数是偶函数.
7．(2023·天津·高考真题（文））将函数的图象向右平移个单位长度，所得图象对应的函数
A．在区间 上单调递增B．在区间 上单调递减
C．在区间 上单调递增D．在区间 上单调递减
答案：A
【解析】
【详解】
分析：首先确定平移之后的对应函数的解析式，然后逐一考查所给的选项是否符合题意即可.
详解：由函数图象平移变换的性质可知：
将的图象向右平移个单位长度之后的解析式为：
.
则函数的单调递增区间满足：，
即，
令可得函数的一个单调递增区间为，选项A正确，B错误；
函数的单调递减区间满足：，
即，
令可得函数的一个单调递减区间为，选项C，D错误；
本题选择A选项.
8．（2023·全国·高考真题（理））关于函数有下述四个结论：
①f(x)是偶函数 ②f(x)在区间（,）单调递增
③f(x)在有4个零点 ④f(x)的最大值为2
其中所有正确结论的编号是
A．①②④B．②④C．①④D．①③
答案：C
【解析】
分析：
化简函数，研究它的性质从而得出正确答案．
【详解】
为偶函数，故①正确．当时，，它在区间单调递减，故②错误．当时，，它有两个零点：；当时，，它有一个零点：，故在有个零点：，故③错误．当时，；当时，，又为偶函数，的最大值为，故④正确．综上所述，①④ 正确，故选C．
【点睛】
画出函数的图象，由图象可得①④正确，故选C．
二、多选题
9．(2023·河北承德·高一阶段练习）将函数图像上所有点的纵坐标伸长为原来的3倍，横坐标缩短为原来的，再将所得的图像向右平移个单位长度，得到函数的图像，则（ ）
A．B．的图像关于直线对称
C．的图像关于点对称D．在上单调递增
答案：BC
【解析】
分析：
由平移和伸缩变换判断A；采用代入法判断BC；由正弦函数的单调性判断D.
【详解】
由题意得，，A错误．，B正确．因为，所以的图像关于点对称，C正确．由，得，所以在上不单调递增，D错误．
故选：BC
10.(2023·全国·模拟预测）将函数的图象向右平移个单位，得到的图象关于y轴对称，则下列说法正确的是（ ）
A．最小正周期的最大值为
B．最小正周期的最大值为
C．当的最小正周期取最大值时，平移后的函数在上单调递增
D．当的最小正周期取最大值时，平移后的函数在上单调递减
答案：AC
【解析】
分析：
先化简，再根据平移法则可得的图象关于y轴对称，即可得到，，，从而可以判断各选项的真假．
【详解】
因为，所以其图象向右平移个单位后得到函数的图象，因为其函数图象关于y轴对称，所以，，所以，，，所以，所以．又因为，令，，所以，，当时，，所以在上单调递增．
故选：AC．
11．(2023·贵州·六盘水市第二中学高一阶段练习）已知函数的部分图像如图所示，则下列说法正确的是（ ）
A．的图像关于点对称B．的图像关于直线对称
C．在上为增函数D．把的图像向右平移个单位长度，得到一个奇函数的图像
答案：ABC
【解析】
分析：
根据函数图像求出函数解析式，然后利用三角函数的性质逐一判断即可.
【详解】
解：由已知，，，，
，，
又，，，
对于A，，故A正确；
对于B，令，得，，时，，故B正确；
对于C，时，令，在上递增，故C正确；
对于D，把的图像向右平移个单位长度，得函数表达式为，它是偶函数，故D错误.
故选：ABC.
12．(2023·全国·南京外国语学校模拟预测）若函数，则下列说法正确的是（ ）
A．函数的图象可由函数的图象向右平移个单位长度得到
B．函数的图象关于直线对称
C．函数的图象关于点对称
D．函数在上为增函数
答案：BD
【解析】
分析：
由三角函数的恒等变换化简，再由三角函数的平移变换可判断A；求出可判断B、C；先判断在上为增函数，即可判断在的单调性.
【详解】
由题意，．
函数的图象向右平移个单位长度可得到，故A错误；，所以函数的图象关于直线对称，故B正确，C错误；
函数在上为增函数，时，，故函数在上单调递增，所以函数在上为增函数，故D正确．
故选：BD．
三、填空题
13．（2023·江苏·高考真题）将函数y=的图象向右平移个单位长度，则平移后的图象中与y轴最近的对称轴的方程是____.
答案：
【解析】
分析：
先根据图象变换得解析式，再求对称轴方程，最后确定结果.
【详解】
当时
故答案为：
14．（2023·长岭县第二中学高三三模）函数的图象关于点_______成中心对称，记函数的最大值为，最小值为，则_______．
答案：
分析：
先将分离常数，找到与奇函数的关系，再利用平移求出对称中心及最大值与最小值之和.
【详解】
，记，
是奇函数，其图象关于坐标原点中心对称.
则的最大值和最小值之和为，
把的图象向上平移一个单位得到的图象，即的图象关于点对称，且．
故答案为：；.
15．(2023·重庆·高考真题（文））将函数图像上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移个单位长度得到的图像，则______.
答案：
【解析】
【详解】
试题分析：
由题意，
所以
所以答案应填：.
16．（2023·山东高三月考）已知定义在上函数（）振幅为2，满足，且．则上零点个数最少为______．
答案：16
分析：
根据题意可得，要使零点个数最少，周期需最大，应为与两个相邻的交点，从而求出，进而求出周期，为了使区间零点最少，将第一个零点放在原点，得出，即可求解.
【详解】
振幅为2，，
，，
要使零点个数最少，周期需最大，
应为与两个相邻的交点，
，
，，，
由，
为了使区间零点最少，将第一个零点放在原点，
，最后个零点恰好在处不在区间中，
，
所以上零点个数最少为16.
故答案为：16
四、解答题
17．(2023·上海市嘉定区第二中学高一期末）已知函数的部分图像如图所示.
(1)求的解析式及对称中心；
(2)先将的图像纵坐标缩短到原来的倍，再向右平移个单位后得到的图像，求函数在上的单调减区间和最值.
答案：(1)，对称中心为，．
(2)单调递减区间为；，．
【解析】
分析：
（1）由函数的图像的顶点坐标求出，由周期求出，由五点法作图求出的值，可得的解析式，再利用三角函数的图像的对称性，得出结论．
（2）由题意利用函数的图像变换规律，求得的解析式，再利用余弦函数的单调性、余弦函数的定义域和值域，得出结论．
(1)
解：根据函数，，的部分图像，
可得，，．
再根据五点法作图，，，故有．
根据图像可得，是的图像的一个对称中心，
故函数的对称中心为，．
(2)
解：先将的图像纵坐标缩短到原来的，可得的图像，
再向右平移个单位，得到的图像，
即，
令，，解得，，
可得的减区间为，，
结合，可得在上的单调递减区间为．
又，故当，时，取得最大值，即；
当，时，取得最小值，即．
18.（2023·天津·静海一中高三月考）已知函数为奇函数，且图象的相邻两对称轴间的距离为.
（1）求的解析式.
（2）求的最大值.
（3）将函数的图象向右平移个单位长度，再把横坐标缩小为原来的(纵坐标变)，得到函数的图象，求的解析式.
答案：（1），（2），（3）
分析：
（1）结合二倍角公式和辅助角公式将函数化简为，再根据正弦函数的周期性奇偶性，分别求出和，从而可求得的解析式
（2）令，则利用换元法可得，从而可求出其最大值，
（3）利用三角函数图象变换规律可求出函数解析式
【详解】
（1）
，
因为图象的相邻两对称轴间的距离为
所以，得，
因为为奇函数，
所以，即，
因为，所以，
所以，
（2），
令，则，
因为对称轴为，
所以当时，取得最大值，
（3）将函数的图象向右平移个单位长度，可得，再把横坐标缩小为原来的(纵坐标变)，得到函数
19．(2023·上海市新场中学高一期末）已知函数，
(1)求函数的最小正周期；
(2)若求的值域；
(3)将函数图象向右平移个单位后，得到函数的图象，求函数的零点.
答案：(1)；
(2)；
(3)或，.
【解析】
分析：
（1）应用降幂公式化简，由正弦函数性质求最小正周期；
（2）根据正弦型函数的性质求的区间值域；
（3）由图象平移得，令结合三角函数的性质求零点即可.
(1)
由，
所以的最小正周期.
(2)
由，则，即，
所以.
(3)
由题设，
令，即，可得，
所以或，，
即或，.
故的零点为或，.
20．(2023·北京·北师大实验中学高一期中）某游乐场的摩天轮示意图如图．已知该摩天轮的半径为30米，轮上最低点与地面的距离为2米，沿逆时针方向匀速旋转，旋转一周所需时间为分钟．在圆周上均匀分布12个座舱，标号分别为1～12（可视为点），现从图示位置，即1号座舱位于圆周最右端时开始计时，旋转时间为t分钟．
(1)当时，求1号座舱与地面的距离；
(2)在前24分钟内，求1号座舱与地面的距离为17米时t的值；
(3)记1号座舱与5号座舱高度之差的绝对值为H米，若在这段时间内，H恰有三次取得最大值，求的取值范围．
答案：(1)
(2)或
(3)
【解析】
分析：
（1）设1号座舱与地面的距离与时间的函数关系的解析式为，，根据所给条件求出、、、，即可得到函数解析式，再令代入计算可得；
（2）由（1）中的解析式，结合正弦函数的性质计算可得；
（3）依题意可得，，从而得到高度差函数，利用两角和差的正弦公式化简，再结合正弦函数的性质求出函数取得最大值时的值，即可得解；
(1)
解：设1号座舱与地面的距离与时间的函数关系的解析式为，，，
则，，
所以
依题意，所以，
当时，所以，故，
所以，
即当时，求1号座舱与地面的距离为；
(2)
解：令，即，
所以，
又，所以，
所以或，解得或，
即或时1号座舱与地面的距离为17米；
(3)
解：依题意，，
所以
令，解，
所以当时取得最大值，
依题意可得
21.(2023·福建·高考真题（文））已知函数．
（1）求函数的最小正周期；
（2）将函数的图象向右平移个单位长度，再向下平移（）个单位长度后得到函数的图象，且函数的最大值为2．
（ⅰ）求函数的解析式； （ⅱ）证明：存在无穷多个互不相同的正整数，使得．
答案：（1）；（2）（ⅰ）； （ⅱ）证明见解析.
【解析】
【详解】
（Ⅰ）因为
．
所以函数的最小正周期．
（Ⅱ）（Ⅰ）将的图象向右平移个单位长度后得到的图象，
再向下平移（）个单位长度后得到的图象．
又已知函数的最大值为，所以，解得．
所以．
（Ⅱ）要证明存在无穷多个互不相同的正整数，使得，
就是要证明存在无穷多个互不相同的正整数，
使得，即．
由知，存在，使得．
由正弦函数的性质可知，当时，均有．
因为的周期为，
所以当（）时，均有．
因为对任意的整数，，
所以对任意的正整数，都存在正整数，使得．
亦即存在无穷多个互不相同的正整数，使得．
22．(2023·上海市嘉定区第一中学高一期末）某小区拟用一块半圆形地块（如图所示）建造一个居民活动区和绿化区．已知半圆形地块的直径千米，点O是半圆的圆心，在圆弧上取点C、D，使得，把四边形ABCD建为居民活动区，并且在居民活动区周围铺上一条由线段AB，BC，CD和DA组成的塑胶跑道，其它部分建为绿化区．设，且；
(1)当时，求四边形ABCD的面积；
(2)求塑胶跑道的总长l关于的函数关系式；
(3)当为何值时，塑胶跑道的总长l最短，并求出l的最小值．（答案保留2位小数）
答案：(1)（平方千米）
(2)
(3)时，塑胶跑道的总长l最短，最小值千米．
【解析】
分析：
（1），，由三角形面积公式求得三个三角形面积后可得四边形面积；
（2），，利用等腰三角形的性质求得底边长，从而得的表达式；
（3）利用二倍角公式化简函数式为关于的二次函数，结合二次函数性质、正弦函数性质得最小值．
(1)
连接，因为，又，则，所以，
，，
所以（平方千米）；
(2)
由（1）知，，，
所以（千米）．
(3)
，
，，所以，即时，．
时，，
，
时，，
所以时，取得最小值千米．