华师大版3.公式法课堂教学ppt课件

这是一份华师大版3.公式法课堂教学ppt课件，共20页。PPT课件主要包含了配方法，知识要点1，典例讲解，知识要点2，求根公式的步骤，公式法等内容，欢迎下载使用。

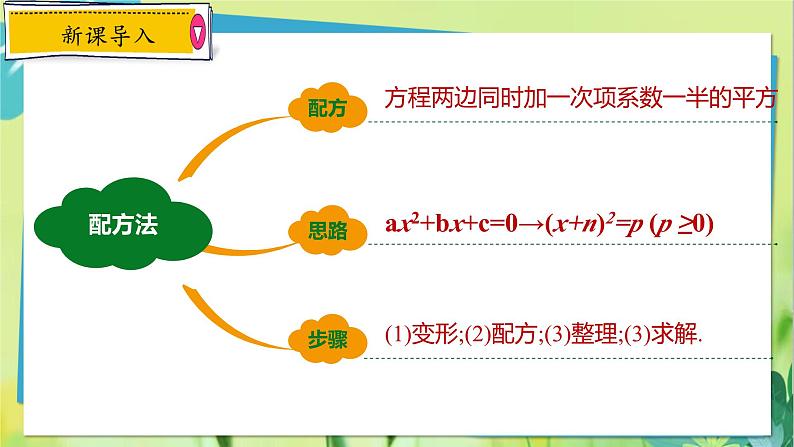
(1)变形;(2)配方;(3)整理;(3)求解.
方程两边同时加一次项系数一半的平方
ax2+bx+c=0→(x+n)2=p (p ≥0)
问题1 用配方法解一般形式一元二次方程 ax2 + bx + c = 0 (a ≠ 0).
(1) b2－4ac ＞0，
则方程有两个不相等的实数根
(2) b2 - 4ac = 0，
(3) b2 - 4ac ＜0，
一元二次方程 ax2 + bx + c = 0 (a ≠ 0)的求根公式：
(1) b2－4ac ≥ 0，
解一个具体的一元二次方程时，把系数直接代入求根公式，可以避免配方过程而直接得出根，这种解法一元二次方程的方法叫做公式法
(1) x2 − 4x − 7 = 0；
例1 用公式法解下列方程
(3) 5x2－3x = x + 1；
(4) x2 + 17 = 8x.
1. 变形：化已知方程变形为一般形式； 2. 定数：确定 a，b，c 各项系数；3. 判定：计算Δ =b2 − 4ac 的值；并判定其符号 4. 计算：若 Δ = b2 − 4ac≥0，则利用求根公式求出； 若 b2 − 4ac＜0，则方程没有实数根.
用公式法解下列一元二次方程：
解：将原方程化为一般形式，得
ax2 + bx + c = 0 (a ≠ 0)
a ≠ 0Δ = b2 − 4ac≥0
1. 变形 2. 定数3. 判定 4. 计算：
1.用公式法解方程 ，得到（ ）
2.已知下列方程，请把它们的序号填在相应最适当的解法后的横线上． ①2(x－1)2＝6； ②(x－2)2＋x2＝4； ③(x－2)(x－3)＝3； ④x2－2x－1＝0； ⑤x2－ x＋ ＝0； ⑥x2－2x－98＝0. (1) 直接开平方法：_____； (2) 配方法：________； (3) 公式法：_____； (4) 因式分解法：___．
3.用适当的方法解下列方程：(1)(x－3)2－25＝0
解：(1)(x－3)2－25＝0.移项，得(x－3)2＝25.开平方，得x－3＝±5，即x－3＝5或x－3＝－5，解得x1＝8，x2＝－2.
(2)(x－2)(x＋1)＝0，∴x－2＝0或x＋1＝0，解得x1＝2，x2＝－1.
(3)移项，得x2＋8x＝－15.配方，得x2＋8x＋16＝1，即(x＋4)2＝1.开平方，得x＋4＝±1，即x＋4＝1或x＋4＝－1，解得x1＝－3，x2＝－5.
(2)x(x－2)＋x－2＝0； (3)x2＋8x＋15＝0.