九年级上册4.一元二次方程根的判别式课堂教学课件ppt

这是一份九年级上册4.一元二次方程根的判别式课堂教学课件ppt，共20页。PPT课件主要包含了配方法，公式法，方程无实数根，知识要点1，反之同样成立，典例讲解，知识要点2，两个不相等的实数根，两个相等的实数根，没有实数根等内容，欢迎下载使用。

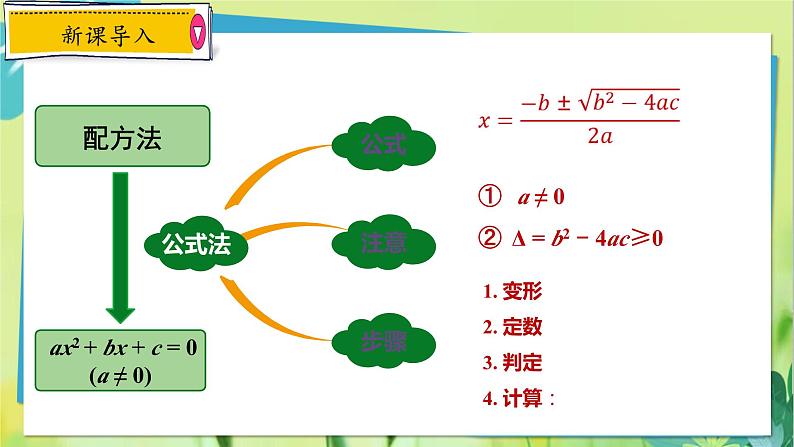
ax2 + bx + c = 0 (a ≠ 0)
a ≠ 0Δ = b2 − 4ac≥0
1. 变形 2. 定数3. 判定 4. 计算：
问题1 不解一元二次方程，判断根的情况？
用配方法解一般形式一元二次方程 ax2 + bx + c = 0 (a ≠ 0).
(1) b2－4ac ＞0，
则方程有两个不相等的实数根
(2) b2 - 4ac = 0，
方程有两个相等的实数根
(3) b2 - 4ac ＜0，
我们把 b2 − 4ac 叫做一元二次方程 ax2 + bx + c = 0 根的判别式，通常用希腊字母“Δ”表示，即 Δ = b2 − 4ac.
当 Δ＞0 时，方程有两个不相等的实数根；
当 Δ = 0 时，方程有两个相等的实数根；
当 Δ＜0 时，方程没有实数根.
一元二次方程 ax2 + bx + c = 0 (a ≠ 0)，
解：(1)原方程可变形为3x2-5x+2=0 因为∆=(-5)2-4×3×2=1>0, 所以方程有两个不相等的实数根。
（3）4(y2+1)-y=0
(3)原方程可变形为4y2-y+4=0 因为∆=(-1)2-4×4=-15<0 所以方程没有实数根。
例2 已知关于x的方程2x2-(3+4k)x+2k2+k=0.(1)当k取何值时，方程有两个不相等的实数根；(2)当k取何值时，方程有两个相等的实数根；(3)当k取何值时，方程没有实数根；
解：a=2，b=-(3+4k)，c=2k2+k∆=[-(3+4k)]2-4×2×(2k2+k)=16k+9
一元二次方程的根的情况的判断的步骤
1.变形:化已知方程为一般形式; 2.定系:用a,b,c写出各项系数;3.计算: 确定b2-4ac的符号; 4.判断：b2-4ac >0 两个不相等的实数根; b2-4ac =0 两个相等的实数根; b2-4ac<0 没有实数根.
不解方程，判断下列方程的根的情况：（1）3x2 + 4x − 3 = 0；
解：（1）a = 3，b = 4，c = −3， ∴ Δ = b2 − 4ac = 42 − 4×3×(−3) = 52＞0. ∴ 方程有两个不相等的实数根．
（2）4x2 = 12x − 9；
（2）方程化为 4x2 − 12x + 9 = 0，a = 4，b = −12，c = 9， ∴ Δ = b2 − 4ac = (−12)2 − 4×4×9 = 0. ∴ 方程有两个相等的实数根．
（3）7y = 5( y2 + 1 ).
（3）方程化为 5y2 −7y + 5 = 0，a = 5，b = −7，c = 5， ∴ Δ = b2－4ac = (−7)2－4×5×5 = −51＜0. ∴ 方程没有实数根．
Δ= b2 − 4ac > 0
Δ= b2 − 4ac = 0
Δ = b2 − 4ac< 0
Δ= b2 − 4ac≥0
注意：1.一元二次方程化为一般式
2. ax2 + bx + c = 0 (a ≠ 0).
1.一元二次方程x2－2x＋3＝0的根的情况是(　　)A．没有实数根B．有两个相等的实数根C．有两个不相等的实数根D．有两个实数根
3.按要求完成下列表格：
4.不解方程，判断下列方程的根的情况：（1）2x2 + 3x − 4 = 0
解：（1）a = 2，b = 3，c = −4， ∴ Δ = b2 − 4ac = 32 − 4×2×(−4) = 41＞0. ∴ 方程有两个不等的实数根．
4.不解方程，判断下列方程的根的情况：（2）x2 − x + = 0；
解：(2)a = 1，b = −1，c = ， ∴ Δ = b2 − 4ac = (−1)2 − 4×1× = 0. ∴ 方程有两个相等的实数根．
4.不解方程，判断下列方程的根的情况：
（3） x2 − x + 1 = 0.
解：（3）x2 − x + 1 = 0，a = 1，b = −1，c = 1， ∴ Δ = b2 − 4ac = (−1)2 − 4×1×1 = −3 < 0. ∴ 方程无实数根．