初中数学浙教版九年级上册第3章 圆的基本性质3.5 圆周角评课课件ppt

这是一份初中数学浙教版九年级上册第3章 圆的基本性质3.5 圆周角评课课件ppt，共26页。PPT课件主要包含了∠PB3Q，知识点，圆周角定义，圆周角定理，O在∠BAC内，O在∠BAC边上，O在∠BAC外，圆周角定理的推论1等内容，欢迎下载使用。

理解圆周角概念，理解圆周用与圆心角的异同；掌握圆周角的性质和直径所对圆周角的特征；能灵活运用圆周角的性质解决问题；发现和证明圆周角定理；会用圆周角定理及推论解决问题.
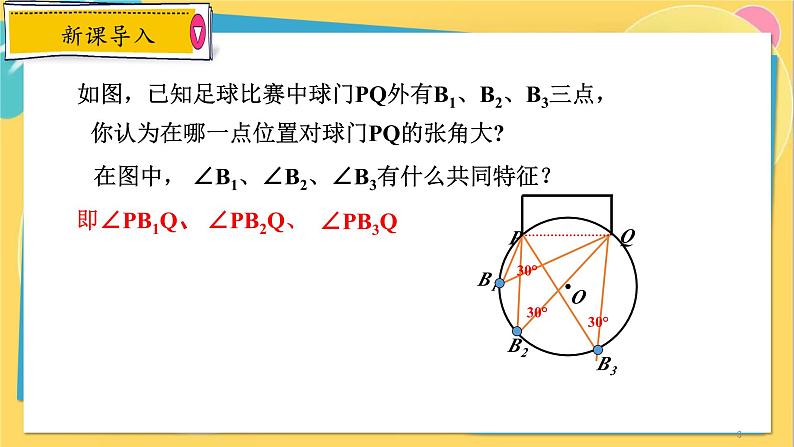
如图，已知足球比赛中球门PQ外有B1、B2、B3三点，
你认为在哪一点位置对球门PQ的张角大?
在图中， ∠B1、∠B2、∠B3有什么共同特征？ 　
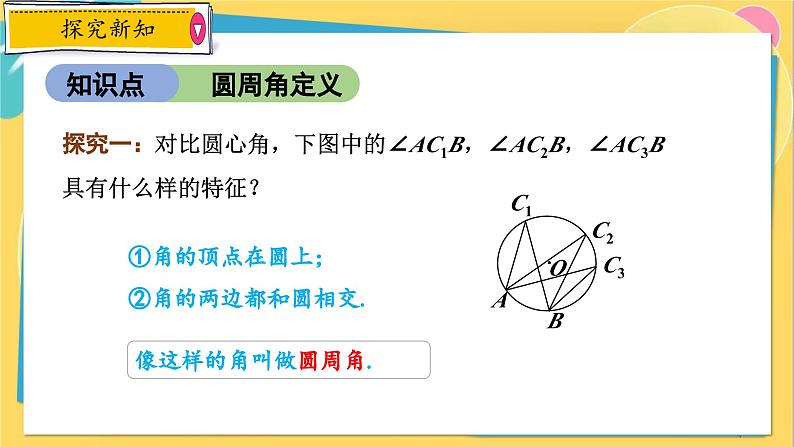
探究一：对比圆心角，下图中的∠AC1B，∠AC2B，∠AC3B 具有什么样的特征？
像这样的角叫做圆周角.
①角的顶点在圆上；②角的两边都和圆相交.
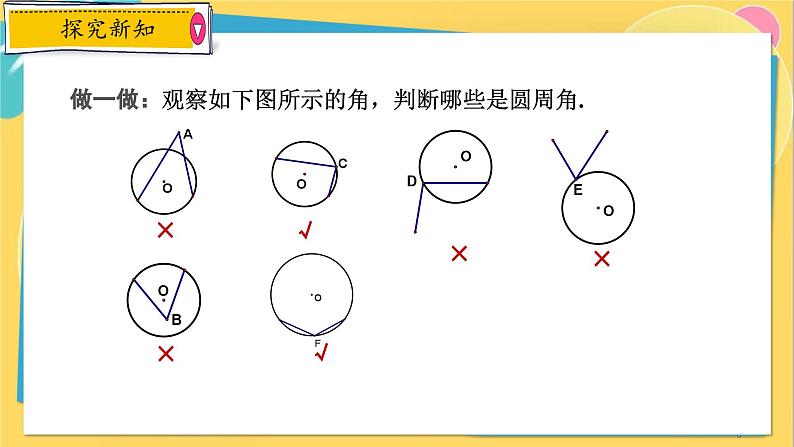
做一做：观察如下图所示的角，判断哪些是圆周角.
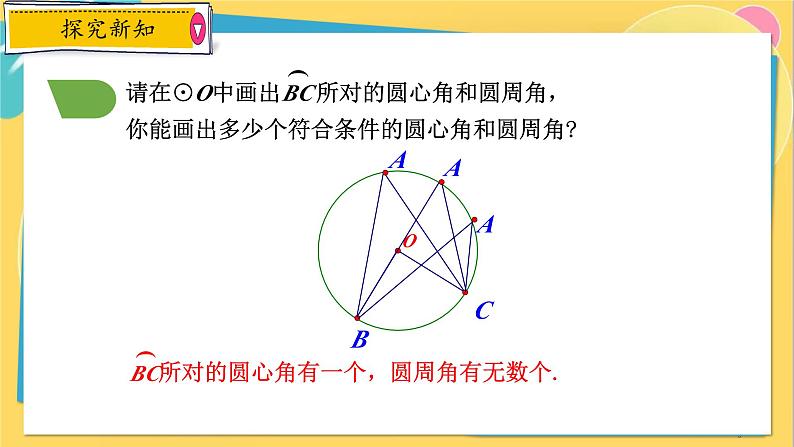
请在⊙O中画出 所对的圆心角和圆周角，你能画出多少个符合条件的圆心角和圆周角?
所对的圆心角有一个，圆周角有无数个.
探究二：动手做一做任意画一个圆，在圆上任取弧AB，并任意画出其所对的两个圆周角及一个圆心角.1.分别量出弧AB所对的圆周角和圆心角的度数，圆周角和圆心角之间有什么关系？2.比较弧AB所对的两个圆周角的度数. 再变动点C在圆周上的位置，圆周角的度数有没有变化. 你发现其中有什么规律吗？  
1.圆周角的度数等于它所对弧上的圆心角度数的一半.2.两个圆周角的度数相等.变动点C在圆周上的位置，圆周角的度数无变化，即同一条弧所对的圆周角相等.
这个结论是否适用于所有情况呢？该怎样证明？
BC所对的圆周角有无数个，观察你所画的图形，它们与圆心O有哪几种位置关系?
【分析】由于圆心有在圆周角内、圆周角外和圆周角的一条边上三类情况，因此需分别对三类不同情况给出证明.
证明：(1)当圆心O在∠BAC的一边AB上时，如图，
(2)当圆心O在∠BAC的内部时，如图，
连结AO并延长，交⊙O于点D.利用(1)的结果，有
(3)当圆心O在∠BAC的外部时，如图，
圆周角定理圆周角的度数等于它所对弧上的圆心角度数的一半.
探究三：如图，若AB是⊙O的直径，那么，∠ACB=____.
反之，若∠ACB是直角，则∠AOB=_____，
所以点A，O，B在一条直线上，AB是⊙O的_______.
由此我们得到圆周角定理的一个推论：
半圆(或直径)所对的圆周角是直角.
90°的圆周角所对的弦是直径.
用于判断某个圆周角是否是直角
用于判断某条弦是否是直径
如图，等腰三角形ABC的顶角∠BAC为50°，以腰AB为直径作半圆，交BC于点D，交AC于点E.求弧BD，弧DE，弧AE的度数.
解：连结BE，AD. ∵AB是圆的直径， ∴∠AEB=∠ADB=90°.∵∠BAC=50°，∴∠ABE=90°－∠BAC=90°－50°=40°.
又∵△ABC是等腰三角形，
如图，点A、B、D、E在⊙O上，弦AE、BD的延长线相交于点C. 若AB是⊙O的直径，D是BC的中点．(1) 试判断AB、AC之间的大小关系，并给出证明；(2) 在上述题设条件下，△ABC还需满足什么条件，点E才一定是AC的中点？(直接写出结论)
(1)试判断AB、AC之间的大小关系，并给出证明；
解： AB＝AC证明：连结AD∵ AB是⊙O的直径∴ ∠ADB＝∠ADC＝90°又∵AD为公共边，BD＝DC∴ Rt△ABD≌Rt△ACD∴ AB＝AC
(2)在上述题设条件下，△ABC还需满足什么条件，点E才一定是AC的中点？(直接写出结论)
解： △ABC为正三角形或AB＝BC或AC＝BC或∠A＝∠B或∠A＝∠C等．
下列图形中的角，是圆周角的是(　　)
如图，某博览会上有一圆形展示区，在其圆形边缘的点P处安装了一台监视器，它的监控角度是55°，为了监控整个展示区，最少需要在圆形边缘上共安装这样的监视器________台．
【2023·株洲】如图，点A，B，C是⊙O上不同的三点，点O在△ABC的内部，连结BO，CO，并延长线段BO交线段AC于点D．若∠A＝60°，∠OCD＝40°，则∠ODC＝________°.